- 16 июля 2025
- 14 минут
- 3 046
Умножение целых чисел: правила, примеры
Статью подготовили специалисты образовательного сервиса Zaochnik.
В этом материале мы покажем, как правильно выполнять умножение целых чисел. Начнем, как всегда, с основных понятий и обозначений и выясним, какой смысл вкладывается в умножение двух целых чисел. Затем сформулируем правила, по которым перемножают целые положительные и целые отрицательные числа, а также числа, имеющие разные знаки. Как всегда, нашу мысль будем пояснять наглядными примерами решений задач. Далее рассмотрим те случаи, когда один из множителей нулевой или равен единице, посмотрим, как можно проверить верность результата, полученного после умножения, а в конце объясним, как правильно перемножать и большее количество целых чисел.
Основные определения при умножении целых чисел
При умножении целых чисел используются те же термины и знаки, о которых мы говорили ранее в статье об умножении натуральных чисел. У нас есть два множителя, которые являются целыми числами, результат, называемый произведением, и знак умножения в виде точки, звездочки или знака "" (в целях единообразия в дальнейшем будем использовать точку).
Если обозначить множители и произведение буквами и, то действие умножения можем записать в виде равенства . Само числовое выражение тоже называется произведением. Произведение двух целых чисел также является целым числом.
В чем состоит смысл умножения целых чисел?
До этого мы уже объясняли смысл умножения на примере натуральных чисел. Произведение натуральных чисел и представляет собой сумму слагаемых, каждое из которых равно .
Целые положительные числа – это натуральные числа, поэтому смысл действия умножения для них точно такой же. В буквенном виде его также можно представить как
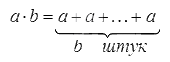
(значения и – целые положительные числа).
В принципе, этот смысл распространяется на все произведения, где одно слагаемое целое и положительное. Второе при этом также должно быть целым, однако оно может быть отрицательным или даже равным нулю. Так, схема умножения числа на будет выглядеть как
Если вторым множителем является единица, то результат умножения – это сумма одного слагаемого, которое равно другому множителю. Это можно записать как . Результат умножения целого числа на единицу есть само это число.
А как быть в случае, если одно из множителей нулевое? Получается, что в ответе будет сумма из слагаемых. Очевидно, что это будет . Запишем, что для любого целого . Умножение целого числа на ноль дает в результате ноль.
В случае с отрицательными числами общий смысл действия умножения сформулировать достаточно сложно. Примем это действие как данность и подчеркнем, что правила умножения в таком случае должны сохранять справедливыми свойства умножения для целых положительных чисел. В частности, такое числовое выражение должно обладать переместительным и сочетательным свойствами.
Основные правила, применяемые при умножении целых чисел
Можно выполнить умножение исходя из того, что оно по сути представляет собой сложение одинаковых слагаемых. Но, как мы уже отмечали, это долгий и трудный процесс, если таких слагаемых у нас много. А если одним из множителей является отрицательное число, то воспользоваться этим способом мы не можем. Поэтому нам надо вывести особые правила для умножения целых чисел. Сформулируем и запишем их.
Как умножать одно целое положительное число на другое
Целые положительные числа относятся к натуральным, поэтому правила умножения натуральных чисел распространяются и на них. В итоге мы, разумеется, получим целый положительный результат, т.е. натуральное число. Разберем конкретные примеры.
Подсчитайте, сколько будет умножить на .
Решение
Обратимся к таблице умножения и возьмем из нее готовый результат.
Получим: .
Ответ: .
Сколько будет умножить на ?
Решение
Представим первый из множителей как сумму разрядных слагаемых, т.е. .
Теперь последовательно умножим слагаемые на данное число: .
Заканчиваем вычисление: .
Ответ: .
Чтобы перемножать многозначные числа, удобно пользоваться методом подсчета в столбик.
Условие: умножьте на .
Решение: запишем множители в столбик и вычислим результат.
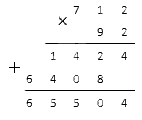
Ответ: .
Как правильно перемножить целые числа, имеющие разные знаки
Для того чтобы вывести правило для такого случая, приведем пример.
Итак, нам надо вычислить произведение числа на . Вспомним смысл умножения и запишем: . Если учесть переместительное свойство, то должно быть верным и . Очевидно, что модуль числа, полученного в результате, соответствует произведению данных множителей. Таким образом, произведение двух чисел с разными знаками есть число отрицательное.
Чтобы умножить одно отрицательное число на одно положительное, надо перемножить между собой модули этих чисел и поставить перед результатом минус.
Разберем несколько примеров, подтверждающих это правило.
Умножьте на .
Решение
Запишем отдельно модули исходных множителей. Получим и . Подсчитаем, чему будет равно их произведение: . Все, что нам нужно сделать дальше, – это поставить знак минуса перед полученным числом.
Ответ: .
Подсчитайте, сколько будет .
Решение
Согласно правилу умножения чисел с разными знаками, нам нужно начать с умножения модулей. Считаем: . Здесь удобно будет воспользоваться методом умножения в столбик. Нам осталось поставить минус перед результатом и записать готовый ответ.
Ответ: .
В последней части параграфа мы попробуем доказать, что равенство справедливо ( и здесь – любые целые числа). Правило умножения целых чисел с разными знаками, которое мы записали выше, является частным случаем этого равенства.
Задача сводится к тому, что нам надо доказать, что значениями выражений и будут противоположные числа. Для этого вычислим сумму . Она будет равна . Учитывая распределительное свойство умножения целых чисел относительно сложения, справедливым будет . Сумма –это ноль, потому что это сумма противоположных чисел, в итоге получается, что . Итоговое произведение равно , согласно свойству умножения целого числа на. Получается, что , значит, и являются противоположными числами. Отсюда вытекает справедливость равенства . Таким же образом можно показать, что .
Как перемножить целые отрицательные числа
Для получения этого правила нам понадобится равенство . Ниже мы приведем его доказательство.
Перед этим мы писали, почему и , следовательно, мы можем записать цепочку равенств .
У нас получилось выражение , которое идентично в силу определения противоположных чисел. Таким образом, .
Теперь мы можем перейти к формулировке правила умножения целых отрицательных чисел.
Чтобы найти произведение целых отрицательных чисел, нам надо вычислить произведение их модулей.
Из правила ясно, что результат умножения двух отрицательных свойств есть число положительное.
Посмотрим, как применить это правило на практике.
Умножьте .
Решение
Воспользуемся правилом и просто перемножим между собой модули: и .
Весь ход решения можно записать как .
Ответ: .
Умножьте на
Решение
Вычисляем модули и перемножаем их столбиком.
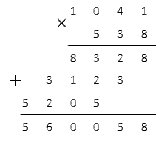
Ответ: .
Как умножить целое число на единицу
Мы уже упоминали, что если мы умножим на единицу любое целое число, то результат будет равен этому же числу, то есть . Так как числовое выражение с умножением обладает переместительным свойством, то тоже должно быть верным. Получается, что . Выведем основное правило и запомним его:
Если умножить два целых числа, одно из которых равно , то результат будет равен второму числу.
К примеру, и . Как видно, от значения второго множителя результат не зависит: произведение и – это , а результат умножения и отрицательного целого числа – это .
Как умножить целое число на нуль
Умножение любого целого числа на нуль дает нам в итоге нулевой результат, т.е. . С учетом переместительного свойства умножения мы получим, что тоже будет верно. Запомним:
Если умножить два целых числа, одно из которых равно , то результат тоже будет равен . Умножение нуля на нуль в итоге также дает нуль.
Так, произведение на – это ; произведение на нуль – тоже нуль; .
Обратное утверждение тоже будет верным: если произведение двух чисел равно нулю, то один или оба множителя тоже равны нулю.
Как проверить результат умножения целых чисел
Для проверки точности результата умножения нам потребуется вспомнить действие деления. Нужно разделить итоговый результат на один из множителей. Если в итоге мы получим второй множитель, то мы все посчитали правильно. Если же результат будет отличен от значения другого множителя, значит, расчет ошибочен и его нужно переделать.
Посмотрим на примерах, как правильно проверить результат умножения целых чисел.
После умножения на получилось . Проверьте, верен ли результат.
Решение
Для проверки нам надо разделить произведение на любой множитель. Возьмем . Делимое и делитель у нас отрицательные, значит, в итоге мы получим частное от деления их модулей: (посмотрите статью о том, как делить целые отрицательные числа).
В итоге мы получим , хотя второй множитель в исходных данных равен . Значит, вычисления были ошибочными.
Ответ: результат деления неверен.
Умножьте на и проверьте точность результата.
Решение
Вспоминаем, как правильно умножать целые отрицательные числа. Считаем: . Теперь переходим к проверке. Для этого делим столбиком результат на любой множитель, например, на .
Согласно правилам деления чисел с разными знаками, сначала мы проводим подсчеты с их модулями: 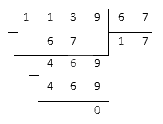
Теперь перед результатом мы должны поставить минус.
У нас получилось , что соответствует первоначальному условию. Значит, мы все сделали правильно.
Ответ: .
Как перемножить три целых числа и более
Зная, что числовое выражение с умножением имеет сочетательное свойство, мы можем точно подсчитать произведение и большего количества множителей. А благодаря остальным свойствам можно сказать, что результат произведения не будет определяться положением множителей в примере и способом расстановки скобок. Ранее мы уже приводили обоснования этих утверждений в случае с натуральными числами. Для примера с целыми множителями эти правила работают таким же образом.
Посмотрим на конкретный пример.
Найдите произведение -ти множителей: и .
Решение
Заменим соседние множители их произведением и запишем, что
С расстановкой скобок можно записать так: . Это позволит нам делать вычисления быстрее и проще.
Можно было переставить множители и по-другому: , в таком случае скобки надо было расставить так: .
Мы видим, что результат будет одинаков вне зависимости от метода расстановки скобок и последовательности вычислений.
Ответ: .
Если хоть один из множителей в примере был бы нулевым, то подсчет не имел бы смысла. Мы сразу могли бы сказать, что результат будет равен . Это не зависит от значения других множителей, они могли бы быть любыми. Обратное утверждение также будет справедливо: если произведение нескольких множителей равно , то один из этих множителей будет нулевым.
Математические онлайн-калькуляторы




