Вычитание десятичных дробей: правила, примеры, решения

Найдите разность $3 , 7 - 0 , 31$.

Решение 

Переписываем десятичные дроби в виде обыкновенных: $3 , 7 = \frac{37}{10}$ и $0 , 31 = \frac{31}{100}$.

Что делать потом, мы уже изучали. Мы получили ответ, который переводим обратно в десятичную дробь: $\frac{339}{100} = 3 , 39$.

Вычислите разность между периодической дробью $0 , \; \left( \; 4 \; \right)$ и периодической десятичной дробью $0 , 41 \; \left( \; 6 \; \right)$.

Решение

 Переведем записи периодических дробей в обыкновенные и подсчитаем.

$0 , 4 \; \left( \; 4 \; \right) = 0 , 4 + 0 , 004 + . . . = \frac{ \; \; 0 \; \; , \; \; 4 \; }{ \; \; 1 \; \; - \; \; 0 \; \; , \; \; 1 \; } = \frac{ \; \; 0 \; \; , \; \; 4 \; }{ \; \; 0 \; \; , \; \; 9 \; } = \frac{4}{9} . \; 0 , 41 \; \left( \; 6 \; \right) = 0 , 41 + \; ( \; 0 \; , \; 006 \; + \; 0 \; , \; 0006 \; + \; . \; . \; . \; ) = \frac{41}{100} + \frac{ \; \; 0 \; \; , \; \; 006 \; }{ \; \; 0 \; \; , \; \; 9 \; } = \; = \frac{41}{100} + \frac{6}{900} = \frac{41}{100} + \frac{1}{150} = \frac{123}{300} + \frac{2}{300} = \frac{125}{300} = \frac{5}{12}$

Итого: $0 , \; \left( \; 4 \; \right) - 0 , 41 \; \left( \; 6 \; \right) = \frac{4}{9} - \frac{5}{12} = \frac{16}{36} - \frac{15}{36} = \frac{1}{36}$  

Если нужно, ответ мы можем представить в виде десятичной дроби: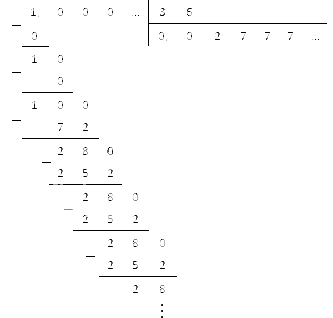

Ответ: $0 , \; \left( \; 4 \; \right) - 0 , 41 \; \left( \; 6 \; \right) = 0 , 02 \; \left( \; 7 \; \right)$. 

Найдите разность $2 , 77369 \dots - 0 , 52$.

Решение

Вторая дробь в условии – конечная, а первая – бесконечная непериодическая. Мы можем округлить ее до четырех знаков после запятой: $2 , 77369 \dots \approx 2 , 7737$. После этого можно выполнять вычитание: $2 , 77369 \dots - 0 , 52 \approx 2 , 7737 - 0 , 52$.

Ответ: $2 , 2537$. 

Найдите разность $4452 , 294 - 10 , 30501$.

Решение 

Для начала выполним первый шаг – уравняем количество десятичных знаков. Допишем два нуля в первую дробь и получим дробь вида $4452 , 29400$, значение которой идентично исходной.

Запишем получившиеся числа друг под другом в нужном порядке, чтобы получился столбик: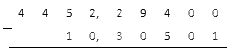

Считаем как обычно, игнорируя запятые: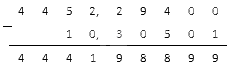

В получившемся ответе поставим запятую в нужном месте: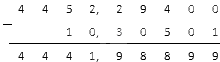

Подсчеты окончены.

Наш результат : $4452 , 294 - 10 , 30501 = 4441 , 98899$.

Вычислите $15 - 7 , 32$.

Решение

Запишем уменьшаемое число $15$ в виде дроби $15 , 00$, поскольку дробь, которую нам нужно вычесть, имеет два знака после запятой. Далее выполняем подсчет столбиком, как обычно: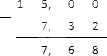

Таким образом, $15 - 7 , 32 = 7 , 68$.

Вычислите разность $1 - 0 , \; \left( \; 6 \; \right)$.

Решение

Указанной в условии периодической десятичной дроби соответствует обычная $\frac{2}{3}$.

Считаем: $1 - 0 , \; \left( \; 6 \; \right) = 1 - \frac{2}{3} = \frac{1}{3}$.

Полученный ответ можно перевести в периодическую дробь $0 , \; \left( \; 3 \; \right)$.

Отнимите$4 , 274 \dots$ от $5$.

Решение 

Указанную бесконечную дробь мы округлим до сотых и получим $4 , 274 \dots \approx 4 , 27$.

После этого вычисляем $5 - 4 , 274 \dots \approx 5 - 4 , 27$.

Преобразуем $5$ в $5 , 00$ и запишем столбик: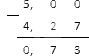

В итоге $5 - 4 , 274 \dots \approx 0 , 73$. 

Найдите разность $37 , 505 \; – 17$.

Решение

Отделяем от дроби целую часть $37$ и вычитаем требуемое число из нее. Получаем $37 , 505 - 17 = 20 , 505$.  

Вычислите разность $0 , 25 - \frac{4}{5}$.

Решение

Представим $0 , 25$ в виде обыкновенной дроби – $0 , 25 = \frac{25}{100} = \frac{1}{4}$.

Теперь нам нужно найти разность между $\frac{1}{4}$и $\frac{4}{5}$.

Считаем: $\frac{4}{5} - 0 , 25 = \frac{4}{5} - \frac{1}{4} = \frac{16}{20} - \frac{5}{20} = \frac{11}{20}$.

Запишем ответ в виде десятичной записи: $0 , 55$. 

Условие: отнимите $0 , \; \left( \; 18 \; \right)$ от $8 \frac{4}{11}$.

Решение

Перепишем периодическую дробь в виде обыкновенной. $0 , \; \left( \; 18 \; \right) = 0 , 18 + 0 , 0018 + 0 , 000018 + . . . = \frac{ \; \; 0 \; \; , \; \; 18 \; }{ \; \; 1 \; \; - \; \; 0 \; \; , \; \; 01 \; } = \frac{ \; \; 0 \; \; , \; \; 18 \; }{ \; \; 0 \; \; , \; \; 99 \; } = \frac{18}{99} = \frac{2}{11}$

Получается, что $8 \frac{4}{11} - 0 , \; \left( \; 18 \; \right) = 8 \frac{4}{11} - \frac{2}{11} = 8 \frac{2}{11}$.

В виде десятичной дроби ответ можно записать как $8 , \; \left( \; 18 \; \right)$. 

Подсчитайте $\frac{9}{40} - 0 , 03$.

Решение 

Заменяем дробь $0 , 03$ на обыкновенную $\frac{3}{100}$.

У нас получается, что: $\frac{9}{40} - 0 , 03 = \frac{9}{40} - \frac{3}{100} = \frac{90}{400} - \frac{12}{400} = \frac{78}{400} = \frac{39}{200}$

Ответ можно оставить так или преобразовать в десятичную дробь $0 , 195$. 

Отнимите $4 , 38475603 \dots .$ из $10 \frac{2}{7}$.

Решение

Преобразуем смешанное число в неправильную дробь.

$10 \frac{2}{7} = \frac{ \; \; 10 \; \; · \; \; 7 \; \; + \; \; 2 \; }{7} = \frac{72}{7}$

Далее эту дробь запишем в десятичном виде и получим $10 , \; \left( \; 285714 \; \right)$.

В итоге $10 \frac{2}{7} - 4 , 38475603. . . = 10 , \; \left( \; 285714 \; \right) - 4 , 38475603. . . \;$. 

Теперь округлим вычитаемые числа до седьмого знака: $10 , \; \left( \; 285714 \; \right) = 10 , 285714285714 \dots \approx 10 , 2857143$ и $4 , 38475603 \dots$$\approx 4 , 3847560$

Тогда $10 , \; \left( \; 285714 \; \right) - 4 , 38475603 \dots \approx 10 , 2857143 - 4 , 3847560$.

Единственное, что осталось сделать – вычесть одну конечную десятичную дробь из другой. Выполним подсчет столбиком: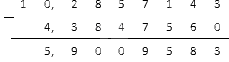

Ответ: $10 \frac{2}{7} - 4 , 38475603. . . \approx 5 , 9009583$