Вычитание натуральных чисел, правила, примеры и решения, правило вычитания числа из суммы

Ранее мы изучали, что такое натуральные числа и какие существуют свойства для того, чтобы производить вычитание. В данной статье представлены основные правила, которые помогут нам выполнять вычитание натуральных чисел. Для того, чтобы информация была понятна и быстро запомнилась, мы снабдили теоретический материал подробно разобранными упражнениями и типичными примерами.

Как связаны сложение и вычитание

Сложение и вычитание тесно связаны. Вычитание – это действие, обратное для сложения. Чтобы усвоить эту информацию, следует рассмотреть подробный пример.

Представим, что в результате сложения предметов $c$ и $b$ , мы получаем предмет $a$ . Исходя из основ сложение натуральных чисел, можно сделать вывод, что $c + b = a$ . Если мы воспользуемся переместительным свойством сложения, то сможем преобразовать полученное равенство как $b + c = a$ . Делаем вывод, что если из а вычесть $b$ , то останется $c$ . Данное равенство $a - b = c$ будет считаться справедливым. По аналогии получаем, что, отняв от $а$ число $c$ , то останется $b$ , то есть, $a - c = b$ .

Благодаря примеру, который мы рассмотрели выше, можно сделать вывод, что если сумма чисел c и b равна a, то число c является разностью натуральных чиселси $b$ , а число $b$ – разностью чисел $a$ и $c$ . То есть, $c = a - b$ и $b = a - c$ , если $c + b = a$ .

Преобразуем данное утверждение и получим важное правило.

Определение 1

Если сумма двух чисел $c$ и $b$ равна a, то разность $a - c$ равна $b$ , а разность $a - b$ равна $c$ .

Теперь мы можем отчетливо увидеть, что сложение и вычитание неразрывно связаны. Исходя из этого факта, можно вывести понятие.

Определение 2

Вычитание – это действие, с помощью которого находится одно слагаемое, когда известна сумма и другое слагаемое.

Данное определение зачастую применяется в различных примерах и задачах.

Как выполнять вычитание с помощью таблицы

Таблица сложения зачастую может быть использована для нахождения суммы двух чисел и для нахождения одного слагаемого в том случае, если известна сумма и другое слагаемое.

Рассмотрим данное утверждение на примере. Рассмотрим упражнение, в котором необходимо найти неизвестное слагаемое, если известно, что второе слагаемое равно $5$ , а сумма равна $8$ .

Это может быть выполнено двумя способами. Воспользуемся графической иллюстрацией, на которой известные числа выделены красным, а найденные – синим.

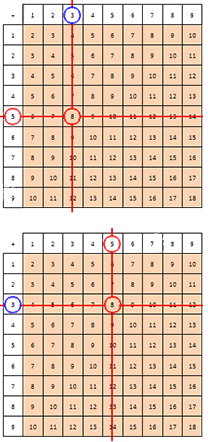
Как выполнять вычитание с помощью таблицы

Рассмотрим несколько способов.

Первый способ. Необходимо найти строку в таблице, известное слагаемое расположено в крайней левой ячейке (берем известное число $5$ ). После этого необходимо найти столбец, пересекающийся с найденной строкой в ячейке. Эта строка должна содержать известную сумму (согласно примеру, число $8$ ). Число, которое нам необходимо найти, расположено в верхней ячейке найденного столбца. Делаем вывод, что число $3$ – это и есть искомое слагаемое.

Второй способ. Необходимо найти в таблице сложения столбец, в верхней ячейке которого располагается известное слагаемое. Находим строчку, пересекающуюся с известным столбцом в ячейке, который соответствует известной сумме. Делаем вывод, что слагаемое, которое требуется найти, расположено в крайней левой ячейке этой строки.

Так, как мы знаем, что сложение и вычитание тесно связаны, эта таблица может быть использована и для поиска разности натуральных чисел. Подробно рассмотрим данную теорию на примере.

Представим, что необходимо вычесть число $7$ из числа $16$ . Делаем вывод, что вычитание сводится к нахождению числа, которое в сумме с числом $7$ даст число $16$ . Воспользуемся использованной выше таблицей.

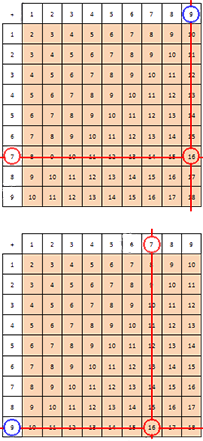
Как выполнять вычитание с помощью таблицы

Вычтя из числа $16$ число $7$ , получаем искомую разность $9$ .

Для того, чтобы пользоваться данной таблицей, рекомендуем заучить информацию и довести процесс нахождения чисел по таблице до автоматизма.

Как производить вычитание разрядов чисел

С помощью таблицы сложения, которую мы рассмотрели выше, можно вычитать десятки из десятков, сотни из сотен, тысячи из тысяч. Так, как мы легко можем работать с простыми числами, так, и по аналогии, можно вычитать десятки и сотни. Например, $6$ сотен минус $2$ сотни равно $4$ сотням, то есть, $600 - 200 = 400$ . Также мы можем использовать таблицу и в других случаях.

Если вспомнить, что одна сотня – это $10$ десятков, одна тысяча – это $10$ сотен, то мы можем вычислять разность, десятков, сотен, тысяч и других чисел.

Рассмотрим пример.

Пример 2

Необходимо вычислить разность $100 - 70$ .

Решение

Преобразуем числа как десятки. Получаем десять десятков и семь десятков. Из таблицы сложения получаем $10 - 7 = 3$ , тогда разность $10$ десятков и $7$ десятков равна $3$ десяткам, то есть, $100 - 70 = 30$ .

Ответ: 30

Пример 3

Необходимо вычислить разность $100000 - 80000$ .

Решение

Так как $100000$ – это $10$ десятков тысяч, а $80000$ – это $8$ десятков тысяч, а $10 - 8 = 2$ . Получаем, что $100000 - 80000 = 20000$ .

Ответ: 20000

Вычитание натурального числа из суммы чисел

Чтобы найти разность суммы двух чисел и числа, необходимо сначала вычислить сумму, из которого вычитается число. Чтобы упростить процесс вычитания, можно воспользоваться определенным свойством вычитания. Рассмотрим несколько примеров.

Пример 4

Необходимо вычесть из суммы $50 + 8$ натуральное число $20$ .

Решение

Сумма $50 + 8$ – это сумма разрядных слагаемых числа $58$ . Ищем варианты решения. Используем приведенное выше правило вычитания: так как $20 < 50$ , то справедливо равенство $(50 + 8) - 20 = (50 - 20) + 8$ . Можем сделать вывод, что $50 - 20 = 30$ ( $5$ десятков – $2$ десятка), тогда $(50 - 20) + 8 = 30 + 8$ . Искомое число $- 38$ .

Решение можно представить в виде цепочки равенств: $(50 + 8) - 20 = (50 - 20) + 8 = 30 + 8 = 38$ .

Ответ: 38

Пример 5

Необходимо вычесть из суммы $21 + 8$ число $3$ .

Решение

Так, как и $3 < 21$ и $3 < 8$ , то справедливы равенства $(21 + 8) - 3 = (21 - 3) + 8$ и $(21 + 8) - 3 = 21 + (8 - 3)$ .

Выберем наиболее подходящий вариант вычисления. Вычитаем из меньшего числа. В примере $8 < 21$ . Итак, $(21 + 8) - 3 = 21 + (8 - 3) = 21 + 5 = 26$ .

Усложним пример. Необходимо вычислить разность числа $20$ из суммы $20000 + 6000 + 300 + 50 + 1$ . Воспользуемся свойством вычитания, которое мы изучили выше.

Вычислить разность довольно легко: $(20000 + 6000 + 300 + 50 + 1) - 20 = 20000 + 6000 + 300 + (50 - 20) + 1 = = 20000 + 6000 + 300 + 30 + 1 = 26331$ .

Рассмотрим решение еще одного примера: $(107 + 42 + 9) - 3 = 107 + 42 + (9 - 3) = 107 + 42 + 6 = 155$ .

Ответ: 26

Вычитание суммы чисел из натурального числа

Определение 2

Чтобы вычесть сумму двух чисел из натурального числа, необходимо вычислить сумму, после чего провести вычитание.

Можно использовать свойство вычитания, приведенное выше. Рассмотрим несколько примеров.

Пример 6

Необходимо вычесть из числа $100$ сумму $90 + 8$ .

Решение

Согласно свойству, получаем: $100 - (90 + 8) = (100 - 90) - 8$ . Находим $100 - 90 = 10$ .

Представим вычисление как: $(100 - 90) - 8 = 10 - 8 = 2$ .

Ответ: 2

Пример 7

Необходимо найти разность числа $17$ и суммы чисел $8$ и $4$ .

Решение

Получаем, что: $17 - (8 + 4) = (17 - 8) - 4$ . Воспользуемся таблицей и получаем, что $17 - 8 = 9,$ тогда $(17 - 8) - 4 = 9 - 4 = 5$ . Можно кратко записать решение как: $17 - (8 + 4) = (17 - 8) - 4 = 9 - 4 = 5$ .

Правая часть равенства $a - (b + c) = (a - b) - c$ иногда записывается в виде $a - (b + c) = a - b - c$ . В этом случае подразумевается, что $a - b - c = (a - b) - c$ . Разность $15 - (7 + 2)$ можно представить, как $15 - 7 - 2$ . Вычисляем разность – отнимаем от $15$ число $7.$ Вычитаем $2$ из полученного результата.

Таким образом, $15 - (7 + 2) = 15 - 7 - 2 = 8 - 2 = 6$ .

Ответ: 6

Используя свойство вычитания и сочетательное свойство сложения, можно найти разность суммы двух, трех и более чисел.

Пример 8

Необходимо выполнить вычитание из числа $1000$ суммы трех чисел вида $900 + 90 + 1$ .

Решение

Сумму $900 + 90 + 1$ представим, как $900$ и $90 + 1$ , то есть, $900 + 90 + 1 = 900 + (90 + 1)$ (изучите подходящий раздел для лучшего понимания). Используем свойство вычитания, изученное выше: $1000 - (900 + (90 + 1)) = (1000 - 900) - (90 + 1)$ . Так как $1000 - 900 = 100, т о (1000 - 900) - (90 + 1) = 100 - (90 + 1)$ . Вычитаем сумму из числа: $100 - (90 + 1) = (100 - 90) - 1 = 10 - 1 = 9$ .

Краткая запись решения имеет вид: $1000 - (900 + 90 + 1) = (1000 - 900) - (90 + 1) = 100 - (90 + 1) = (100 - 90) - 1 = 10 - 1 = 9$

Разность $1000 - (900 + 90 + 1)$ также может выглядеть как $((1000 - 900) - 90) - 1$ . Можно записать это по-другому как $1000 - 900 - 90 - 1$ . В этих случаях сначала находится разность первых двух чисел, далее от полученного результата вычитается третье число и так далее.

Ответ: 9

Пример 9

Необходимо вычесть из числа $20$ сумму чисел $10, 4, 3$ и $1$ .

Решение

Получаем, что: $20 - (10 + 4 + 3 + 1) = 20 - 10 - 4 - 3 - 1 = 10 - 4 - 3 - 1 = 6 - 3 - 1 = 3 - 1 = 2$ .

Ответ: 2

Вычитание единиц из десятков, сотен, тысяч

От числа $10$ можно любое число от $1$ до $9$ . Используем таблицу, представленную выше. Но что делать в других случаях? Необходимо уменьшаемое представить, как сумму двух слагаемых, одно из которых равно $10$ , после чего вычесть его из суммы. Закрепим знание материала примером:

Пример 10

Необходимо вычесть из $60$ число $5$ .

Решение

Число $60$ представляем в виде суммы двух чисел, одно из которых равно $10$ . Второе числа находим, вычитая из $60$ число $10$ . Так как $60 - 10 = 50$ , то $60 = 50 + 10$ . Заменим $60$ суммой $50 + 10$ , получая $60 - 5 = (50 + 10) - 5.$ Получаем, что: $(50 + 10) - 5 = 50 + (10 - 5) = 50 + 5 = 55$ .

Ответ: 5

Рассмотрев вычитание единиц из десятков, перейдем к вычитанию единиц из сотен.

Чтобы из $100$ вычесть число от $1$ до $10$ нужно $100$ представить, как $90 + 10$ и прибегнуть к правилу.

Пример 11

Необходимо найти разность $100 - 7$ .

Решение

Представим $100$ как $90 + 10$ и выполняем: $100 - 7 = (90 + 10) - 7 = 90 + (10 - 7) = 90 + 3 = 93$ . Усложним пример. Отнимем от числа $500$ число $3$ . Представим $500$ в виде суммы. Второе слагаемое $= 500 - 100$ , то есть, $400$ . Имеем $500 = 400 + 100$ . $100 = 90 + 10, 500 = 400 + 90 + 10$ .

Таким образом, $500 - 3 = (400 + 90 + 10) - 3$ .

Закончим вычисление: $(400 + 90 + 10) - 3 = 400 + 90 + (10 - 3) = 400 + 90 + 7 = 497$ .

Ответ: 93

Перейдем к вычитанию единиц из тысяч.

Пример 12

Необходимо вычислить разность $1000 - 8.$

Решение

Так как $1000 = 900 + 100$ , а $100 = 90 + 10$ , то $1000 = 900 + 90 + 10$ .

Тогда $1000 - 8 = (900 + 90 + 10) - 8 = 900 + 90 + (10 - 8) = 900 + 90 + 2 = 992$ .

Ответ: 992

Пример 13

Необходимо вычесть из $7000$ единицу.

Решение

$7000$ запишем как $7000 = 6000 + 1000 = 6000 + 900 + 100 = 6000 + 900 + 90 + 10$ .

Делаем вывод:
$7000 - 1 = (6000 + 900 + 90 + 10) - 1 = 6000 + 900 + 90 + (10 - 1) = 6000 + 900 + 90 + 9 = 6999$ .

Ответ: 6999

Используя данный пример, мы сможем вычитать любые числа, также тысячные и десятитысячные.

Пример 14

Необходимо вычислить разность $100000 - 4$ .

Решение

Так как
$100000 = 90000 + 10000 = 90000 + 9000 + 1000 = = 90000 + 9000 + 900 + 100 = 90000 + 9000 + 900 + 90 + 10$
то
$100000 - 4 = (90000 + 9000 + 900 + 90 + 10) - 4 = = 90000 + 9000 + 900 + 90 + (10 - 4) = 90000 + 9000 + 900 + 90 + 6 = 99996$ .

Ответ: 99996

Пример 15

Необходимо вычесть из $4000000$ число $5$ .

Решение

Так как
$4000000 = 3000000 + 1000000 = 3000000 + 900000 + 100000 = = 3000000 + 900000 + 90000 + 10000 = 3000000 + 900000 + 90000 + 9000 + 1000 = = 3000000 + 900000 + 90000 + 9000 + 900 + 100 = = 3000000 + 900000 + 90000 + 9000 + 900 + 90 + 10$
то
$4000000 - 5 = (3000000 + 900000 + 90000 + 9000 + 900 + 90 + 10) - 5 = = 3000000 + 900000 + 90000 + 9000 + 900 + 90 + (10 - 5) = = 3000000 + 900000 + 90000 + 9000 + 900 + 90 + 5 = 3999995$ .

Ответ: 3999995

Вычитание единиц из произвольных чисел

Будем считать, что уменьшаемое можно представить в виде суммы разрядных слагаемых. Подобные случаи мы рассматривали в предыдущих параграфах.

Определение 3

Чтобы вычесть из такого числа однозначное число, нужно уменьшаемое разложить по разрядам, после чего вычесть число из суммы.

Рассмотрим типичные примеры, которые помогут усвоить материал.

Пример 16

Необходимо определить разность чисел $46$ и $2$ .

Решение

Число $46$ представляем как $40 + 6$ , тогда $46 - 2 = (40 + 6) - 2 = 40 + (6 - 2) = 40 + 4 = 44$ . Для того, чтобы усложнить задание, найдем разность $46$ и $8$ . Имеем $46 - 8 = (40 + 6) - 8$ . Так как $8$ больше, чем $6$ , то: (

$(40 + 6) - 8 = (40 - 8) + 6 \cdot (40 - 8),$

вычислим по примеру: $40 - 8 = (30 + 10) - 8 = 30 + (10 - 8) = 30 + 2 = 32$ . Тогда $(40 - 8) + 6 = 32 + 6 = 38$ . Теперь отнимем от $6047$ число $5$ . Раскладываем $6047$ и вычитаем число из суммы: $6047 - 5 = (6000 + 40 + 7) - 5 = 6000 + 40 + (7 - 5) = 6000 + 40 + 2 = 6042$

Ответ: 6042

Закрепим навыки еще одним примером.

Пример 17

Необходимо вычесть из числа $2503$ число $8$ .

Решение

Раскладываем и получаем: $2503 - 8 = (2000 + 500 + 3) - 8$ . Так как $8$ больше, чем $3$ , но меньше, чем $500$ , то $(2000 + 500 + 3) - 8 = 2000 + (500 - 8) + 3$ . Вычислим разность $500 - 8$ , для этого представляем число 500 в виде суммы $400 + 100 = 400 + 90 + 10$ (при необходимости вернитесь к предыдущему пункту этой статьи) и выполняем необходимые вычисления:
$500 - 8 = (400 + 90 + 10) - 8 = 400 + 90 + (10 - 8) = 400 + 90 + 2 = 492. 2000 + (500 - 8) + 3 = 2000 + 492 + 3 = 2495$ .

Ответ: 2495

Вычитание из произвольных натуральных чисел

Чтобы вычесть десятки, сотни из числа, нужно уменьшаемое представить как сумму и выполнить вычитание. Разберем данный процесс на нескольких примерах.

Пример 18

Найдем разность $400$ и $70$ .

Решение

Разложим $400$ как $300 + 100$ . Тогда $400 - 70 = (300 + 100) - 70$ . Согласно свойству, получим: $(300 + 100) - 70 = 300 + (100 - 70) = 300 + 30 = 330$ . Также можем отнять от числа $1000$ число $40$ . Представим, что $1000 - 40 = (900 + 100) - 40 = 900 + (100 - 40) = 900 + 60 = 960$ .

Согласно правилу, $(7000 + 900 + 100) - 10 = 7000 + 900 + (100 - 10) = 7000 + 900 + 90 = 7990$ .

Ответ: 7990

Пользуемся этим правилом в аналогичных случаях.

Пример 19

Найдем $400000 - 70$ .

Решение

$400000$ разложим как $300000 + 90000 + 9000 + 900 + 100$ , тогда
$400000 - 70 = (300000 + 90000 + 9000 + 900 + 100) - 70 = 300000 + 90000 + 9000 + + 900 + (100 - 70) = 300000 + 90000 + 9000 + 900 + 30 = 399993$

Ответ: 399993

Воспользуемся схожим принципов для вычисления сотен, тысяч и других.

Пример 20

Найдем $5000 - 800$ .

Решение

Представим $5000$ как $4000 + 1000$ . Тогда $5000 - 800 = (4000 + 1000) - 800$ . Используем свойство: $(4000 + 1000) - 800 = 4000 + (1000 - 800)$ . Так как тысяча – это десять сотен, то $1000 - 800 = 200$ . Таким образом, $4000 + (1000 - 800) = 4000 + 200 = 4200.$

Ответ: 4200

Данное правило можно использовать для вычисления. Запомнить его, оно еще не раз вам пригодится.

Пример 21

Найдем разность $140$ и $40$ .

Решение

Так как $140 = 100 + 40$ , то $140 - 40 = (100 + 40) - 40$ . Получаем: $(100 + 40) - 40 = 100 + (40 - 40) = 100 + 0 = 100 (40 - 40) = 0$ в силу свойств, а $100 + 0 = 100$ .

Найдем $140 - 60$ . Имеем $140 - 60 = (100 + 40) - 60$ . Так как $60$ больше, чем $40$ , то: $(100 + 40) - 60 = (100 - 60) + 40 = 40 + 40 = 80$ .

Ответ: 80

Вычитание произвольных чисел

Рассмотрим правило, когда вычитаемое раскладывается по разрядам. После представления числа в виде суммы разрядных слагаемых используется свойство вычитания, описанное выше. Вычитание начитается с единиц, потом десятков, сотен и так далее.

Пример 22

Вычислим $45 - 32$ .

Решение

Разложим $32$ по разрядам: $32 = 30 + 2$ . Имеем $45 - 32 = 45 - (30 + 2)$ . Представим, как $45 - (30 + 2) = 45 - (2 + 30)$ . Теперь применяем свойство вычитания суммы из числа: $45 - (2 + 30) = (45 - 2) - 30$ . Осталось вычислить $45 - 2$ , после чего отнять число $30$ .

Усвоив предыдущие правила, вы легко выполните это.

Итак, $45 - 2 = (40 + 5) - 2 = 40 + (5 - 2) = 40 + 3 = 43$ . Тогда $(45 - 2) - 30 = 43 - 30$ . Осталось представить уменьшаемое в виде суммы разрядных слагаемых и закончить вычисления: $43 - 30 = (40 + 3) - 30 = (40 - 30) + 3 = 10 + 3 = 13$

Все решение удобно записывать в виде цепочки равенств:
$45 - 32 = 45 - (2 + 30) = (45 - 2) - 30 = ((40 + 5) - 2) - 30 = = (40 + (5 - 2)) - 30 = (40 + 3) - 30 = (40 - 30) + 3 = 10 + 3 = 13$

Немного усложним пример.

Вычтем из числа $85$ число $18$ .

Раскладываем по разрядам число $18$ , при этом получаем $18 = 10 + 8$ . Меняем местами слагаемые: $10 + 8 = 8 + 10.$ Теперь вычитаем полученную сумму разрядных слагаемых из числа $85$ и применяем свойство вычитания суммы из числа: $85 - 18 = 85 - (8 + 10) = (85 - 8) - 10$ . Вычисляем разность в скобках:
$85 - 8 = (80 + 5) - 8 = (80 - 8) + 5 = ((70 + 10) - 8) + 5 = (70 + (10 - 8)) + 5 = (70 + 2) + 5 = 70 + 7 = 77$

Тогда $(85 - 8) - 10 = 77 - 10 = (70 + 7) - 10 = (70 - 10) + 7 = 60 + 7 = 67$

Ответ: 67

Для закрепления материала разберем решение еще одного примера.

Пример 23

Отнимем от числа $23555$ число $715$ .

Решение

Так как $715 = 700 + 10 + 5 = 5 + 10 + 700 = 5 + (10 + 700)$ , то $23555 - 715 = 23555 - (5 + 10 + 700) .$ Вычитаем сумму из числа следующим образом: $23555 - (5 + (10 + 700)) = (23555 - 5) - (10 + 700)$ .

Вычислим разность в скобках:
$23555 - 5 = (20000 + 3000 + 500 + 50 + 5) - 5 = 20000 + 3000 + 500 + 50 + (5 - 5) = = 20000 + 3000 + 500 + 50 + 0 = 20000 + 3000 + 500 + 50 = 23550.$

Тогда $(23555 - 5) - (10 + 700) = 23550 - (10 + 700)$ .

Еще раз обращаемся к свойству вычитания натурального числа из суммы: $23550 - (10 + 700) = (23550 - 10) - 700$ .
$(23550 - 10) - 700 = 23540 - 700 = (20000 + 3000 + 500 + 40) - 700 = = 20000 + (3000 - 700) + 500 + 40$

Вычтем из $3000$ число $700$ и : $3000 - 700 = (2000 + 1000) - 700 = 2000 + (1000 - 700) = 2000 + 300 = 2300$ , тогда $20000 + (3000 - 700) + 500 + 40 = 20000 + 2300 + 500 + 40 = 22840$ .

Ответ: 22840

Вычитание чисел на координатном луче

Рассмотрим, что такое вычитание геометрической точки зрения. Используем координатный луч. Вычитание из $a$ числа $b$ на координатном луче находится так: определяем точку, координатой является $a$ . Откладываем в направлении точки $O$ единичные отрезки в количестве, определяемом вычитаемым $b$ . Так мы найдем точку на координатном луче, координата равна разности $a - b$ . Другими словами, это перемещение влево из точки с координатой a на расстояние $b$ , попадая в точку с координатой $a - b$ .

Рассмотрим вычитание на координатном луче с помощью рисунка. Так мы попадем в точку с координатой $2$ так, что $6 - 4 = 2$ .

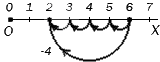
Вычитание чисел на координатном луче

Проверка результата вычитания сложением

Проверка результата вычитания двух натуральных чисел базируется на связи между вычитанием и сложением. Там мы выяснили, что если $c + b = a$ , то $a - b = c$ и $a - c = b$ . Если $a - b = c$ , то $c + b = a$ ; если $a - c = b$ , то $b + c = a$ . Докажем справедливость данных равенств.

Пусть из $a$ отложили в сторону $b$ , после чего осталось $c$ . Этому действию соответствует равенство $a - b = c$ . Мы вернем отложенные $b$ на место, то плучим $a$ . Тогда можно говорить о справедливости равенства $c + b = a$ .

Теперь мы можем сформулировать правило, позволяющее проверить результат вычитания сложением: нужно к полученной разности прибавить вычитаемое, при этом должно получиться число, равное уменьшаемому. Если полученное число не равно уменьшаемому, то при вычитании допущена ошибка.

Осталось лишь разобрать решения нескольких примеров, в которых выполняется проверка результата вычитания при помощи сложения.

Пример 24

Из $50$ было вычтено $42$ и было получено $6$ . Правильно ли было выполнено вычитание?

Решение

Проверим полученный результат вычитания. Для этого прибавим к полученной разности вычитаемое: $6 + 42 = 48$ (если нужно, изучите другие параграфы по данной теме). Так как мы получили число, не равное уменьшаемому $50$ , то можно утверждать, что вычитание было проведено неправильно. Была допущена ошибка.

Ответ: неправильно

Пример 25

Необходимо определить разность $1024 - 11$ и проверить результат.

Решение

Вычисляем разность: $1024 - 11 = 1024 - (1 + 10) = (1024 - 1) - 10 = 1023 - 10 = 1013$ .

Теперь выполняем проверку:

$1013 + 11 = (1000 + 10 + 3) + (10 + 1) = = 1000 + 10 + 10 + 3 + 1 = 1000 + 20 + 4 = 1024$

Получили число, равное уменьшаемому, следовательно, разность вычислена правильно. $1024 - 1 = 1023$ .

Ответ: 1013

Проверка результата вычитания вычитанием

Правильность результата вычитания натуральных чисел можно проверить не только с помощью сложения, но и с помощью вычитания. Для этого нужно от уменьшаемого отнять найденную разность. При этом должно получиться число, равное вычитаемому. В противном случае в вычисления была допущена ошибка.

Рассмотрим данное правило подробнее. Это позволит осуществить проверку результата вычитания чисел вычитанием. Представим, что у нас есть $a$ фруктов, среди которых $b$ яблок и $c$ груш. Если мы отложим яблоки, то у нас останется только $c$ груш, при этом имеем $a - b = c$ . Если бы мы отложили все груши, то у нас остались бы только $b$ яблок, при этом $a - c = b$ .

Пример 26

От числа $543$ было отнято число $343$ , в результате было получено число $200$ . Проверить результат.

Решение

Выполните проверку.

Вспоминаем о связи вычитания и сложения: $200 + 343 = 543$ . От уменьшаемого $543$ отнимаем разность $200$ , получаем $543 - 200 = (500 + 43) - 200 = (500 - 200) + 43 = 30 + 43 = 343$ .

Это число равно вычитаемому, вычитание выполнено верно.

Ответ: верно