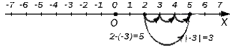Статью подготовили специалисты образовательного сервиса Zaochnik.
Вычитание смешанных чисел: правила, примеры, решения
- 17 октября 2023
- 9 минут
- 7
Для полноценного разбора темы статьи введем термины и определения, обозначим смысл действия вычитания и выведем правило, согласно которому действие вычитания возможно привести к выполнению действия сложения. Разберем практические примеры. А также рассмотрим действие вычитания в геометрическом толковании – на координатной прямой.
В общем, основные термины, используемые для описания действия вычитания, едины для любого типа чисел.
Уменьшаемое – целое число, из которого будет производиться вычитание.
Вычитаемое – целое число, которое будем вычитать.
Разность – результат выполненного действия вычитания.
Для обозначения самого действия используется знак минус, размещённый между уменьшаемым и вычитаемым. Все составные части действия, указанные выше, записываются в виде равенства. Т.е., если заданы целые числа и , и при вычитании из первого второго получается число , действие вычитания запишется следующим образом: .
Выражение вида также будем обозначать как разность, как и само конечное значение этого выражения.
Смысл вычитания целых чисел
В теме вычитания натуральных чисел была установлена взаимосвязь между действиями сложения и вычитания, которая дала возможность определить вычитание как поиск одного из слагаемых по известной сумме и второму слагаемому. Примем, что вычитание целых чисел имеет такой же смысл: по заданной сумме и одному из слагаемых определяется второе слагаемое.
Указанный смысл действия вычитания целых чисел дает возможность утверждать, что и , если , где – целые числа.
Рассмотрим простые примеры для закрепления теории:
- пусть мы знаем, что , тогда разность ;
- допустим, известно, что , тогда , а .
Правило вычитания целых чисел
Указанный выше смысл действия вычитания не обозначает для нас конкретного способа вычислить разность. Т.е. мы можем утверждать, что одно из известных слагаемых – результат вычитания из суммы другого известного слагаемого. Но, если одно из слагаемых окажется неизвестным, то мы не можем знать, какова будет разность между суммой и известным слагаемым. Следовательно, для выполнения действия вычитания нам потребуется правило вычитания целых чисел:
Для того, чтобы определить разность двух чисел, необходимо к уменьшаемому прибавить число, противоположное вычитаемому, т.е. , где и – целые числа; и – противоположные числа.
Докажем указанное правило вычитания, т.е. докажем справедливость указанного в правиле равенства. Для этого, согласно смыслу вычитания целых чисел, прибавим к вычитаемое и убедимся, что получим в результате уменьшаемое a, т.е. проверим действительность равенства . На основании свойств сложения целых чисел мы можем записать цепочку равенств: , она и будет являться доказательством правила вычитания целых чисел.
Рассмотрим применение правила вычитания целых чисел на конкретных примерах.
Вычитание целого положительного числа, примеры
Необходимо выполнить вычитание из целого числа целого положительного числа .
Решение
Согласно правилу, чтобы из заданного числа вычесть целое положительное число , нужно к уменьшаемому прибавить число , т.е. противоположное заданному . Таким образом, искомая разность будет равна сумме целых чисел и . Вычислив нужную сумму чисел с противоположными знаками, получим число . Т.е. итогом вычитания числа из числа будет число . Запишем все решение в одну строку: .
Ответ: .
Необходимо вычесть из целого отрицательного числа целое положительное число .
Решение
Согласно правилу, прибавим к уменьшаемому числу число (т.е. противоположное заданному вычитаемому ). Найдем сумму целых отрицательных чисел: . Таким образом, искомая разность равна . Все решение запишем так: .
Ответ: .
Вычитание нуля, примеры
Правило вычитания целых чисел дает возможность вывести принцип вычитания нуля из целого числа – вычитание нуля из любого целого числа не изменяет это число, т.е. = a, где – произвольное целое число.
Поясним. Согласно правилу вычитания, вычитание нуля – это прибавление к уменьшаемому числа, противоположного нулю. Нуль – число, противоположное самому себе, т.е. вычесть нуль это то же самое, что прибавить нуль. На основе соответствующего свойства сложения прибавление нуля к любому целому числу не изменяет это число. Таким образом,
.
Рассмотрим простые примеры вычитания нуля из различных целых чисел. Например, разность равна . Если же из целого отрицательного числа вычесть нуль, то получится . Если от нуля отнять нуль, получим нуль.
Вычитание целого отрицательного числа, примеры
Необходимо вычесть из целого числа целое отрицательное число .
Решение
Согласно правилу вычитания определение разности необходимо произвести прибавлением к уменьшаемому числу числа, противоположного вычитаемому . Тогда:
Ответ:
Определить разность .
Решение
Произведем вычитание из целого отрицательного числа целого отрицательного числа . Для этого вычислим сумму двух чисел: уменьшаемого и числа (т.е. противоположного заданному вычитаемому ). Получим: .
Ответ: .
Вычитание равных целых чисел
Если заданные уменьшаемое и вычитаемое равны, то их разность будет равна нулю, т.е., где – любое целое число.
Поясним. Согласно правилу вычитания целых чисел , что означает: чтобы из целого числа вычесть равное ему, нужно прибавить к этому числу число, ему противоположное, что даст в результате нуль.
Например, разность равных целых чисел и равна нулю; совершая действие вычитания из числа числа , получаем нуль; отнимая от нуля нуль, получаем также нуль.
Проверка результата вычитания целых чисел
Необходимая проверка производится с помощью действия сложения. Для этого к полученной разности прибавляем вычитаемое: в итоге должно получится число, равное уменьшаемому.
Было произведено вычитание целого числа из целого числа , при этом получена разность . Верно ли было произведено вычитание?
Решение
Выполним проверку согласно указанному выше принципу. Прибавим к заданной разности вычитаемое: . Мы получили число, отличное от заданного уменьшаемого, следовательно, была допущена ошибка при вычислении разности.
Ответ: нет, вычитание было произведено неверно.
Вычитание целых чисел на координатной прямой
В заключение рассмотрим геометрическое толкование действия вычитания целых чисел. Начертим горизонтальную координатную прямую, направленную вправо:

Выше мы вывели правило совершения действия вычитания, согласно ему: , тогда геометрическое толкование вычитания чисел и будет совпадать с геометрическим смыслом сложения целых чисел и . Из этого следует, что для вычитания из целого числа a целого числа , необходимо:
- сдвинуться из точки с координатой на единичных отрезков влево, если – положительное число;
- сдвинуться из точки с координатой на (модуль числа ) единичных отрезков вправо, если – отрицательное число;
- остаться в точке с координатой , если .
Рассмотрим на примере с применением графического изображения:
Пусть необходимо вычесть из целого числа целое положительное число . Для этого, согласно вышеуказанной схеме, переместимся влево на единичных отрезка, попадая, таким образом, в точку с координатой , т.е. .
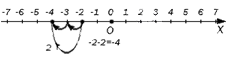
Еще один пример: вычитаем из целого числа целое отрицательное число . Тогда, согласно схеме, переместимся вправо на единичных отрезка, попадая, таким образом, в точку с координатой . Получаем равенство: и иллюстрацию к нему: