Признак делимости на 8, примеры, доказательство

Содержание:

27 декабря 2023
10 минут
4687

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

В статье рассматривается признак делимости на $8$ с приведением его формулировки и примерами.

Признак делимости на 8, примеры

Формулировка звучит так: если число, составленное из последних цифр в записи целого $а$ , делится на $8$ тогда и все число делится на $8$ ; когда число, составленное из трех последних, не делится на $8$ , тогда и все число не делится на число $8$ .

Приведенная формулировка говорит о том, что этот признак применим только для четырехзначных, пятизначных и так далее чисел. Данный метод безопасный и удобный, так как после всего можно выполнить проверку. Установка деления на $8$ производится при помощи деления выражения на $8$ .

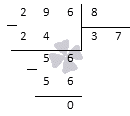
Признак делимости на 8, примеры — Пример 1

Когда последние три цифры имеют вид $024, 086, 002, 008$ , тогда необходимо отбросить нули и выполнять деление двузначных чисел.

Пример 2

При помощи признака делимости на $8$ узнать, делится ли $920 072$ на $8$ .

Решение

Видно, что последние три цифры записываются как $072$ , значит, будем иметь дело с числом $72$ , разделим его на $8$ . По признаку делимости видно, что заданное число делится на $8$ без остатка.

Пример 3

Определить числа, которые поделятся на $8$ из заданных $- 900 007, 21 008, - 111 008$ и $732 237 001$ .

Решение

Воспользовавшись признаком делимости на $8$ , нужно пересмотреть все цифры, находящиеся справа числа, то есть $007, 008, 008, 001$ . Отсюда видно, что будем работать с числами $7, 8, 8, 1$ . Очевидно, что только 8 поделится само на себя, значит, из выбранных только $21008$ и $- 111008$ поделятся на $8$ .

Ответ: $- 900 007$ и $732 237 001$ на $8$ не делятся, а $21 008$ и $- 111 008$ делятся на $8$ .

Когда записанное число имеет справа последние три цифры нули, то есть $23000, - 980000$ , тогда очевидно, что все число делится на $8$ . Рассмотрим доказательство данного утверждения.

Число $1000$ можно представить как $1 000 = 8 \cdot 125$ . Видно, что оно точно поделится на $8$ .

Когда имеются числа, где в конце записаны $3$ нуля, то очевидно, что нужно использовать правило умножения натуральных чисел на $1000$ , которое поможет представить $а$ в виде $a = a_{1} \cdot 1 000$ . Отсюда видно, что $a_{1}$ получим из числа $а$ , когда заберем последние три цифры, расположенные справа. Очевидно, что $1000$ делится на $8$ , тогда и выражение $a_{1} \cdot 1 000$ будет делиться на $8$ по свойствам делимости. Отсюда получили, что число $а$ будет делиться на $8$ без остатка.

Теперь делимость числа на $8$ доказана, когда число оканчивается на три нуля. Благодаря свойству делимости, это утверждение верно для всех натуральных $а$ .

Доказательство признака делимости на 8

Для доказательства делимости на $8$ необходимо использовать представление натурального числа $а$ , то есть любое число представить в виде $a = a_{1} \cdot 1 000 + a_{0}$ , где $a_{1}$ – это результат отбрасывания последних трех цифр, а $a_{0}$ – это есть последние цифры числа $а$ . Для полного понятия запишем, что $234 698 = 234 \cdot 1 000 + 698$ .

Для доказательства нужно применять свойства делимости:

для деления нацело числа $а$ на $b$ необходимо и достаточно, чтобы модель числа $а$ делился на модуль числа $b$ ;
когда из равенства $a = s + t$ все члены могут делиться на $b$ , тогда и заданный член делится на $b$ .

Переходим к доказательству признака делимости на $8$ с достаточными и необходимыми условиями.

Теорема 1

Чтобы целое число поделилось на $8$ , необходимо и достаточно, чтобы число, состоящее из последних трех цифр записи числа $а$ , делилось на $8$ .

Доказательство 1

Пусть целое число обозначим за $а$ . Тогда модуль числа $а$ является натуральным числом. Необходимо представить его в виде $|a| = a_{1} \cdot 1000 + a_{0}$ .

Перейдем к доказательству необходимости. Пусть число $а$ делится на $8$ . Тогда нужно составить такое число, которое будет составлено из тех последних цифр заданного числа $а$ , делящееся на $8$ Отсюда получим, что $a_{0}$ делится на $8$ .

Если $а$ делится на $8$ , тогда и его модуль тоже, исходя из первого свойств делимости. Исходя из равенства вида $|a| = a_{1} \cdot 1000 + a_{0}$ получим, что $a_{1} \cdot 1 000$ поделится на $8$ , $а$ по второму свойству делимости видно, что $a_{0}$ поделится на $8$ без остатка. Необходимость доказана.

Доказательство достаточности начинается с того, что необходимо взять за a₀число, которое делится на $8$ . Это приведет к тому, что и число $а$ будет делиться на $8$ .

Видно, что из равенства $|a| = a_{1} \cdot 1000 + a_{0}$ произведение вида $a_{1} \cdot 1 000$ поделится на $8$ , что означает, $a_{0}$ также будет делиться на $8$ . Делаем вывод, что и само число будет делиться на $8$ . Достаточность доказана.

Другие случаи делимости на 8

Не всегда возможно установить делимость на $8$ сразу, так как либо число, либо выражение не представлено в явном виде. Поэтому следует предварительно выполнить несколько преобразований.

Когда имеется буквенное выражение $а$ , следует выяснить, будет ли выражение делиться на $8$ , возникают трудности. В этом случае, исходя из свойства, все выражение должно делиться на $8$ . Рассмотрим на примере.

Чаще всего, если имеется произведение, лучше применять формулу бинома Ньютона.

Пример 4

Выяснить, делится ли выражение вида $9^{n} + 16 n - 9$ на $8$ при $n$ являющимся натуральным числом.

Решение

Нужно представить $9$ как $8 + 1$ и применить формулу бинома Ньютона. Тогда получаем выражение:

$9^{n} + 16 n - 9 = (8 + 1) + 16 n - 9 = = (C_{n}^{0} \cdot 8^{n} + C_{n}^{1} \cdot 8^{n - 1} \cdot + . . . + + C_{n}^{n - 2} \cdot 8^{2} \cdot 1^{n - 2} + C_{n}^{n - 1} \cdot 8 \cdot 1^{n - 1} + C_{n}^{n} \cdot 1^{n}) + 16 n - 9 = = (8^{n} + C_{n}^{1} \cdot 8^{n - 1} + . . . + C_{n}^{n - 2} \cdot 8^{2} + n \cdot 8 + 1) + 16 n - 9 = = 8^{n} + C_{n}^{1} \cdot 8^{n - 1} + . . . + C_{n}^{n - 2} \cdot 8^{2} + 24 n - 8 = = 8 \cdot (8^{n - 1} + C_{n}^{1} \cdot 8^{n - 2} + . . . + C_{n}^{n - 2} \cdot 8^{1} + 3 n - 1)$

Получили результат, который делится на $8$ , потому как имеется множитель в виде числа $8$ , причем значение в скобках равняется натуральному числу $n$ . Отсюда получаем, что данное по условию выражение будет делиться на $8$ при любому натуральном значении $n$ .

Ответ: да.

Заданное выражение можно разложить на множители или оно уже задается в таком виде. Следует учитывать то, что значение выражения с $n$ при $n = 8 \cdot m, n = 8 \cdot m + 1, \dots, n = 8 \cdot m + 7$ , где $m$ является целым числом, будет делиться на $8$ , тогда и само заданное выражение поделится на $8$ при любом целом значении $n$ .

Пример 5

Доказать, что выражение вида $n^{5} + 7 \cdot n^{3}$ будет делиться на $8$ при любом целом значении $n$ .

Решение

Перейдем к разложению на множители выражения $n^{5} + 7 \cdot n^{3} = n^{3} \cdot (n^{2} + 7)$

Если $n = 8 m$ , тогда получим, что:

$n^{3} \cdot (n^{2} + 7) = (8 m)^{3} \cdot ({(8 m)}^{2} + 7) = 8^{3} \cdot m^{3} \cdot (64 m^{2} + 7)$

Выражение будет делиться на m без остатка при любом целом значении числа m, потому как имеется множитель вида $8^{3}$ ^,который тоже делится на $8$ .

Когда $n = 8 \cdot m + 1$ , получим, что

$n^{3} \cdot (n^{2} + 7) = (8 m)^{3} \cdot ({(8 m)}^{2} + 7) = (8 m + 1)^{3} \cdot (64 m^{2} + 16 m + 8) = = (8 m + 1)^{3} \cdot 8 \cdot (8 m^{2} + 2 m + 1)$

Значение такого произведения делится на $8$ , когда m принимает значение любого целого числа, потому как в записи имеется множитель $8$ .

Таким же образом выполняется при $n = 8 \cdot m + 2, n = 8 \cdot m + 3, \dots, n = 8 \cdot m + 7$ , тогда получаем, что произведения также поделятся на $8$ .

Мы доказали, что выражение, заданное по условию, будет делиться на $8$ без остатка при любом целом $n$ .

Имеются случаи, когда необходимо применять метод математической индукции.

Пример 6

Доказать при помощи математической индукции, что при $n$ , равному любому натуральному числу, выражение вида $9^{n} + 16 n - 9$ будет делиться на $8$ .

Решение

Необходимо провести проверку при значении $n = 1$ , чтобы исходное выражение делилось на $8$ Тогда получим, что $9^{1} + 16 \cdot 1 - 9 = 16$ . Очевидно, что результат, равный $16$ , делится на $8$ без остатка.

Если предположить, что значение $n = k$ , тогда выражение вида $9^{n} + 16 n - 9$ делится на $8$ и приобретает вид $9^{k} + 16 k - 9$ , который также делится на число $8$ .

По заданному предположению необходимо доказать, что $9^{k} + 16 k - 9$ поделится на $8$ , а исходное выражение поделится на $8$ при значении $n = k + 1$ .

Тогда получим, что:

$9^{k + 1} + 16 \cdot (k + 1) - 9 = 9 \cdot 9^{k} + 16 k + 7 = 9 \cdot (9^{k} + 16 k - 9) - 128 k + 88 = = 9 \cdot (9^{k} + 16 k - 9) - 8 \cdot (16 k - 11)$

Видно, что полученная разность выражений вида $9 \cdot (9^{k} + 16 k - 9)$ будет делиться на $8$ , потому как $9^{k} + 16 k - 9$ поделится на $8$ , а произведение $8 \cdot (16 k - 11)$ , исходя из выше написанного, также поделится на $8$ , потому как имеет множитель в виде числа $8$ . Отсюда следует, что полученная разность поделится на $8$ . Видно, что искомая делимость на $8$ найдена из выражения вида $9^{k + 1} + 16 \cdot (k + 1) - 9$ .

Данный пример был решен при помощи метода математической индукции, была доказана делимость выражения $9^{n} + 16 n - 9$ на $8$ без остатка, где $n$ является любым целым натуральным числом.

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.