Простые и составные числа, определения, примеры, таблица простых чисел, решето Эратосфена

Содержание:

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.

Простые и составные числа – определения и примеры

Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.

Определение 1

Простыми числами называют целые числа, которые больше единицы и имеют два положительных делителя, то есть себя и $1$ .

Определение 2

Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.

Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.

Определение 3

Простые числа – это натуральные числа, имеющие только два положительных делителя.

Определение 4

Составное число – это натуральное число, имеющее более двух положительных делителей.

Любое число, которое больше $1$ является либо простым, либо составным. Из свойства делимости имеем, что $1$ и число а всегда будут делителями для любого числа $а$ , то есть оно будет делиться само на себя и на $1$ . Дадим определение целых чисел.

Определение 5

Натуральные числа, которые не являются простыми, называют составными.

Простые числа: $2, 3, 11, 17, 131, 523$ . Они делятся только сами на себя и на $1$ . Составные числа: $6, 63, 121, 6697$ . То есть число $6$ можно разложить на $2$ и $3$ , а $63$ на $1, 3, 7, 9, 21, 63$ , а $121$ на $11, 11$ , то есть его делители будут $1, 11, 121$ . Число $6697$ разложится на $37$ и $181$ . Заметим, что понятия простых чисел и взаимно простых чисел – разные понятия.

Таблица простых чисел

Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:

Таблица простых чисел

Таблица для всех существующих натуральных чисел нереальна, так как их существует бесконечное множество. Когда числа достигают размеров $10000$ или $1000000000$ , тогда следует задуматься об использовании решета Эратосфена.

Рассмотрим теорему, которая объясняет последнее утверждение.

Теорема 1

Наименьший положительный и отличный от $1$ делитель натурального числа, большего единицы, является простым числом.

Доказательство 1

Возьмем, что а является натуральным числом, которое больше $1$ , $b$ является наименьшим отличным от единицы делителем для числа $а$ . Следует доказать, что $b$ является простым числом при помощи метода противного.

Допустим, что $b$ – составное число. Отсюда имеем, что есть делитель для $b$ , который отличен от $1$ как и от $b$ . Такой делитель обозначается как $b_{1}$ . Необходимо, чтобы условие $1 < b_{1} < b$ было выполнено.

Из условия видно, что $а$ делится на $b$ , $b$ делится на $b_{1}$ , значит, понятие делимости выражается таким образом: $a = b \cdot q$ и $b = b_{1} \cdot q_{1}$ , откуда $a = b_{1} \cdot (q_{1} \cdot q)$ , где $q$ и $q_{1}$ являются целыми числами. По правилу умножения целых чисел имеем, что произведение целых чисел – целое число с равенством вида $a = b_{1} \cdot (q_{1} \cdot q)$ . Видно, что $b_{1}$ – это делитель для числа $а$ . Неравенство $1 < b_{1} < b$ не соответствует, потому как получим, что $b$ является наименьшим положительным и отличным от $1$ делителем $а$ .

Теорема 2

Простых чисел бесконечно много.

Доказательство 2

Предположительно возьмем конечное количество натуральных чисел $n$ и обозначим как $p_{1}, p_{2}, \dots, p_{n}$ . Рассмотрим вариант нахождения простого числа, отличного от указанных.

Примем на рассмотрение число р, которое равняется $p_{1}, p_{2}, \dots, p_{n} + 1$ . Оно не равняется каждому из чисел, соответствующих простым числам вида $p_{1}, p_{2}, \dots, p_{n}$ . Число р является простым. Тогда считается, что теорема доказана. Если оно составное, тогда нужно принять обозначение $p_{n + 1}$ и показать несовпадение делителя ни с одним из $p_{1}, p_{2}, \dots, p_{n}$ .

Если это было бы не так, тогда, исходя из свойства делимости произведения $p_{1}, p_{2}, \dots, p_{n}$ _,получим, что оно делилось бы на $p_{n + 1}$ . Заметим, что на выражение $p_{n + 1}$ делится число р равняется сумме $p_{1}, p_{2}, \dots, p_{n} + 1$ . Получим, что на выражение $p_{n + 1}$ должно делиться второе слагаемое этой суммы, которое равняется $1$ , но это невозможно.

Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел. Отсюда следует, что простых чисел бесконечно много.

Так как простых чисел очень много, то таблицы ограничивают числами $100, 1000, 10000$ и так далее.

Решето Эратосфена

При составлении таблицы простых чисел следует учитывать то, что для такой задачи необходима последовательная проверка чисел, начиная с $2$ до $100$ . При отсутствии делителя оно фиксируется в таблицу, если оно составное, то в таблицу не заносится.

Рассмотрим пошагово.

Если начать с числа $2$ , то оно имеет только $2$ делителя: $2$ и 1, значит, его можно занести в таблицу. Также и с числом $3$ . Число $4$ является составным, следует разложить его еще на $2$ и $2$ . Число $5$ является простым, значит, можно зафиксировать в таблице. Так выполнять вплоть до числа $100$ .

Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.

Способ при помощи решета Эратосфена считают самым удобным. Рассмотрим на примере таблиц, приведенных ниже. Для начала записываются числа $2, 3, 4, \dots, 50$ .

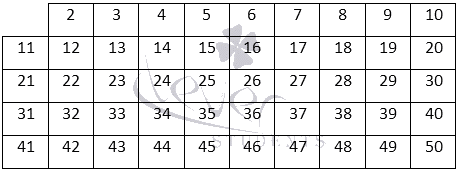
Решето Эратосфена

Теперь необходимо зачеркнуть все числа, которые кратны $2$ . Произвести последовательное зачеркивание. Получим таблицу вида:

Решето Эратосфена

Далее вычеркиваем все числа, кратные $3$ . Получаем таблицу вида:

Решето Эратосфена

Переходим к вычеркиванию чисел, кратных $5$ . Получим:

Решето Эратосфена

Вычеркиваем числа, кратные $7, 11$ . В конечном итоге таблица получает вид

Решето Эратосфена

Перейдем к формулировке теоремы.

Теорема 3

Наименьший положительный и отличный от $1$ делитель основного числа а не превосходит $\sqrt{a}$ , где $\sqrt{a}$ является арифметическим корнем заданного числа.

Доказательство 3

Необходимо обозначить $b$ наименьший делитель составного числа $а$ . Существует такое целое число $q$ , где $a = b \cdot q$ , причем имеем, что $b \leq q$ . Недопустимо неравенство вида $b > q$ , так как происходит нарушение условия. Обе части неравенства $b \leq q$ следует умножить на любое положительное число $b$ , не равное $1$ . Получаем, что $b \cdot b \leq b \cdot q$ , где $b^{2} \leq a$ и $b \leq \sqrt{a}$ .

Из доказанной теоремы видно, что вычеркивание чисел в таблице приводит к тому, что необходимо начинать с числа , которое равняется $b^{2}$ и удовлетворяет неравенству $b^{2} \leq a$ . То есть, если вычеркнуть числа, кратные $2$ , то процесс начинается с $4$ , а кратных $3$ – с $9$ и так далее до $100$ .

Составление такой таблицы при помощи теоремы Эратосфена говорит о том, что при вычеркивании всех составных чисел, останутся простые, которые не превосходят $\sqrt{n}$ . В примере, где $n = 50$ , у нас имеется, что $\sqrt{n} = \sqrt{50}$ . Отсюда и получаем, что решето Эратосфена отсеивает все составные числа, которые по значению не больше значения корня из $50$ . Поиск чисел производится при помощи вычеркивания.

Данное число простое или составное?

Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.

Пример 1

Доказать что число $898989898989898989$ является составным.

Решение

Сумма цифр заданного числа равняется $9 \cdot 8 + 9 \cdot 9 = 9 \cdot 17$ . Значит, число $9 \cdot 17$ делится на $9$ , исходя из признака делимости на $9$ . Отсюда следует, что оно составное.

Такие признаки не способны доказать простоту числа. Если нужна проверка, следует производить другие действия. Самый подходящий способ – это перебор чисел. В течение процесса можно найти простые и составные числа. То есть числа по значению не должны превосходить $\sqrt{a}$ . То есть число а необходимо разложить на простые множители. если это будет выполнено, тогда число а можно считать простым.

Данное число простое или составное? — Пример 2

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.