- 16 июля 2025
- 11 минут
- 4 000
Разложение чисел на простые множители, способы и примеры разложения
Статью подготовили специалисты образовательного сервиса Zaochnik.
Данная статья дает ответы на вопрос о разложении числа на простыне множители. Рассмотрим общее представление о разложении с примерами. Разберем каноническую форму разложения и его алгоритм. Будут рассмотрены все альтернативные способы при помощи использования признаков делимости и таблицы умножения.
Что значит разложить число на простые множители?
Разберем понятие простые множители. Известно, что каждый простой множитель – это простое число. В произведении вида имеем, что у нас простых множителя в виде .
Разложение на множители предполагает его представление в виде произведений простых. Если нужно произвести разложение числа , тогда получим . Запись примет вид . Не исключено, что множители могут повторяться. Такое число как имеет .
Не все числа предрасположены к разложению. Числа, которые больше и являются целыми можно разложить на множители. Простые числа при разложении делятся только на и на самого себя, поэтому невозможно представить эти числа в виде произведения.
При , относящемуся к целым числам, представляется в виде произведения и , где делится на и на . Составные числа раскладывают на простые множители при помощи основной теоремы арифметики. Если число больше , то его разложение на множители принимает вид . Разложение предполагается в единственном варианте.
Каноническое разложение числа на простые множители
При разложении множители могут повторяться. Их запись выполняется компактно при помощи степени. Если при разложении числа а имеем множитель , который встречается раз и так далее раз. Таким образом разложение примет вид a=p1s1·. Эта запись имеет название канонического разложения числа на простые множители.
При разложении числа получим, что ,его канонический вид будет . При помощи канонического разложения можно найти все делители числа и их количество.
Алгоритм разложения числа на простые множители
Чтобы правильно разложить на множители необходимо иметь представление о простых и составных числах. Смысл заключается в том, чтобы получить последовательное количество делителей вида чисел , это дает возможность получить , где , где , где . При получении , то равенство получим искомое разложение числа на простые множители. Заметим, что .
Для нахождения наименьших общих делителей необходимо использовать таблицу простых чисел. Это выполняется на примере нахождения наименьшего простого делителя числа . При взятии простых чисел и так далее, причем на них делим число . Так как не является простым числом, следует учитывать, что наименьшим простым делителем не будет больше . Видно, что не существуют делителей , тогда понятно, что является простым числом.
Рассмотрим на примере числа . При его делении на имеем, что с остатком равным . Отсюда следует, что делителем не может являться, деление должно производиться нацело. При делении на получим, что . Отсюда вывод – является наименьшим простым делителем числа .
При разложении на простые множители необходимо пользоваться таблицей простых чисел, где . При разложении следует использовать около простых чисел, а при около .
Рассмотрим алгоритм разложения на простые множители:
- нахождение наименьшего множителя при делителе числа a по формуле , когда , тогда а является простым числом и включено в разложение на множители, когда не равняется , тогда и следуем к пункту, находящемуся ниже;
- нахождение простого делителя числа при помощи последовательного перебора простых чисел, используя , когда , тогда разложение примет вид , когда , тогда , причем производим переход к следующему шагу;
- перебор простых чисел и нахождение простого делителя числа по формуле , когда , тогда получим, что , когда не равняется , тогда и производим переход к следующему шагу;
- производится нахождение простого делителя числа при помощи перебора простых чисел с , а также , где , шаг является завершающим, в итоге получаем, что .
Результат алгоритма записывается в виде таблицы с разложенными множителями с вертикальной чертой последовательно в столбик. Рассмотрим рисунок, приведенный ниже.
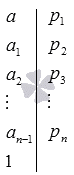
Полученный алгоритм можно применять при помощи разложения чисел на простые множители.
Примеры разложения на простые множители
Во время разложения на простые множители следует придерживаться основного алгоритма.
Произвести разложение числа на простые множители.
Решение
Для того, чтобы найти наименьший простой делитель, необходимо перебрать все простые числа, имеющиеся в . То есть . Деление без остатка, значит это первый простой делитель, который обозначим как . Получаем, что . Пришли к равенству вида , где . Тогда , то есть следует перейти к следующему шагу.
Остановимся на нахождении простого делителя числа . Следует перебрать простые числа, то есть (ост. ). Так как деление с остатком, что не является делителем. При выборе числа получаем, что . Значит, что является наименьшим простым делителем по . Получим равенство вида в виде . Имеем, что не равно , тогда следует переходит дальше.
Наименьший простой делитель числа ищется при помощи перебора чисел, начиная с . Получим, что (ост. ). Отсюда видно, что не делится на , потому как (ост. ), (ост. ) и (ост. ). Видно, что является простым числом. По формуле выглядит так: . Получили, что , что означает завершение алгоритма. Теперь множители записываются в виде .

Ответ: .
Разложить число на простые множители.
Решение
Первый шаг предусматривает разложение на простые множители и , где .
Второй шаг предполагает, что , и не простые делители для числа , а простой делитель, потому как . Получаем, что . Очевидно, что .
Нахождение наименьшего простого делителя к числу равняется . Видно, что , поэтому .
Для нахождения простого делителя числа используем число , то есть . Тогда получим выражение вида , и .
Для числа число является наименьшим простым делителем. Отсюда . Тогда . Это указывает на завершение алгоритма. Множители запишутся в виде .
Каноническая запись ответа примет вид .
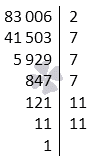
Ответ: .
Произвести разложение числа на множители.
Решение
Для нахождения первого простого множителя произвести перебор простых чисел, начиная с . Конец перебора приходится на число . Тогда и .
Второй шаг алгоритма заключается в переборе меньших простых чисел. То есть начинаем с числа . Число можно считать простым, потому как оно является простым делителем числа . Отсюда получаем, что , то и .
Третий шаг говорит о том, что является простым числом, так как не имеет ни одного простого делителя, который не превосходит . Примерное значение подкоренного выражения имеет вид . Иначе запишем как . Отсюда видно, что и . Получим, что разложение числа на простые множители получается как .
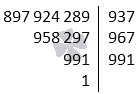
Ответ: .
Использование признаков делимости для разложения на простые множители
Чтобы разложить число на простые множители, нужно придерживаться алгоритма. Когда имеются небольшие числа, то допускается использование таблицы умножения и признаков делимости. Это рассмотрим на примерах.
Если необходимо произвести разложение на множители , то по таблице видно: . Получившиеся числа и являются простыми, поэтому они являются простыми множителями для числа .
Если необходимо произвести разложение числа , то по таблице видно: . Но и – это не простые множители, так как их можно еще разложить как и . Тогда полное разложение отсюда получается как . Каноническая запись примет вид .
При разложении числа можно пользоваться признаками делимости. В данном случае актуальны признаки делимости на и на . Отсюда получаем, что , где можно разделить на , то есть записать в виде , а значит, что . Основываясь на признаке делимости получаем, что . Все множители простые. Каноническое разложение принимает вид .
Когда мы находим простые множители, необходимо использовать признаки делимости и таблицу умножения. Если представить число в виде произведения множителей, то необходимо учитывать правило делимости на . Получим, что , причем . То есть искомое разложение пример вид произведения .
Математические онлайн-калькуляторы




