- 16 июля 2025
- 7 минут
- 14 584
Непрерывность функции в точке, разрывы первого и второго рода
Статью подготовили специалисты образовательного сервиса Zaochnik.
Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.
Непрерывность функции в точке
Функция является непрерывной в точке , если предел слева равен пределу справа и совпадает со значением функции в точке , т.е.:
Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.
Дана функция . Необходимо доказать ее непрерывность в точке .
Решение
В первую очередь, определим существование предела слева. Чтобы это сделать, используем последовательность аргументов , сводящуюся к . Например, такой последовательностью может быть:
Соответствующая последовательность значений функций выглядит так:
на чертеже они обозначены зеленым цветом.
Достаточно очевидно, что такая последовательность сводится к , значит .
Определим существование предела справа: используем последовательность аргументов , сводящуюся к . Например, такой последовательностью может быть:
Соответствующая последовательность функций:
на рисунке обозначена синим цветом.
И эта последовательность сводится к , тогда .
Действиями выше было показано, что пределы справа и слева являются равными, а значит существует предел функции в точке , при этом .
После вычисления значения функции в заданной точке очевидно выполнение равенства:
что свидетельствует о непрерывности заданной функции в заданной точке.
Покажем графически:
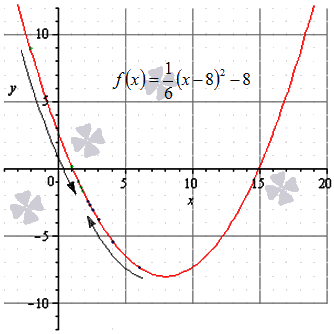
Ответ: Непрерывность функции в заданной части доказано.
Устранимый разрыв первого рода
Функция имеет устранимый разрыв первого рода в точке , когда пределы справа и слева равны, но не равны значению функции в точке, т.е.:
Задана функция . Необходимо определить точки ее разрыва и определить их тип.
Решение
Сначала обозначим область определения функции:
В заданной функции точкой разрыва может служить только граничная точка области определения, т.е. . Исследуем функцию на непрерывность в этой точке.
Выражение упростим: .
Определим пределы справа и слева. Поскольку функция является непрерывной при любом действительном , тогда:
Ответ: пределы справа и слева являются равными, а заданная функция в точке не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.
Неустранимый разрыв первого рода
Неустранимый разрыв первого рода также определяется точкой скачка функции.
Функция имеет неустранимый разрыв первого рода в точке , когда пределы справа и слева не являются равными, т.е.: . Точка здесь – точка скачка функции.
Задана кусочно-непрерывная функция . Необходимо изучить заданную функцию на предмет непрерывности, обозначить вид точек разрыва, составить чертеж.
Решение
Разрывы данной функции могут быть лишь в точке или в точке .
Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:
- слева от точки заданная функция есть , тогда в силу непрерывности линейной функции: ;
- непосредственно в точке функция принимает вид: , тогда: ;
- на промежутке заданная функция есть: . Опираясь на свойство непрерывности квадратичной функции, имеем:
- в точке функция имеет вид: и .
- справа от точки заданная функция есть . В силу непрерывности линейной функции:
Ответ: в конечном счете мы получили:
- - это означает, что в точке заданная кусочная функция непрерывна;
- - таким образом, в точке определён неустранимый разрыв первого рода (скачок).
Нам остается только подготовить чертеж данного задания.
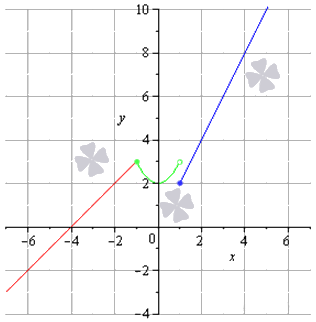
Разрыв второго рода (бесконечный разрыв)
Функция имеет разрыв второго рода в точке , когда какой-либо из пределов слева или справа не существует или бесконечен.
Задана функция . Необходимо исследовать заданную функцию на непрерывность, определить вид точек разрыва, подготовить чертеж.
Решение
Запишем область определения функции: .
Найдем пределы справа и слева от точки .
Зададим произвольную последовательность значений аргумента, сходящуюся к слева. К примеру:
Ей соответствует последовательность значений функции:
Очевидно, что эта последовательность является бесконечно большой отрицательной, тогда .
Тепереь зададим произвольную последовательность значений аргумента, сходящуюся к справа. К примеру: , и ей соответствует последовательность значений функции:
Эта последовательность - бесконечно большая положительная, а значит .
Ответ: точка - точка разрыва функции второго рода.
Проиллюстрируем:
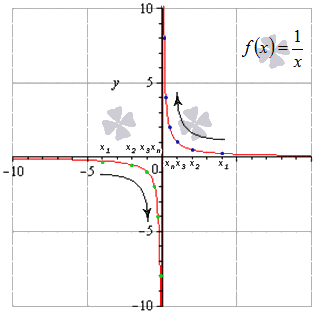
Математические онлайн-калькуляторы




