- 7 августа 2025
- 15 минут
- 4 033
Преобразование графиков элементарных функций
Статью подготовили специалисты образовательного сервиса Zaochnik.
Основные элементарные функции в чистом виде без преобразования встречаются редко, поэтому чаще всего приходится работать с элементарными функциями, которые получили из основных с помощью добавления констант и коэффициентов. Такие графики строятся при помощи геометрических преобразований заданных элементарных функций.
Рассмотрим на примере квадратичной функции вида , графиком которой является парабола , которая сжата втрое относительно и симметрична относительно , причем сдвинутую на по вправо, на единицы по вверх. На координатной прямой это выглядит так:
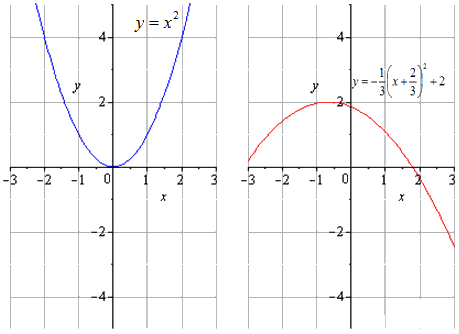
Геометрические преобразования графика функции
Применяя геометрические преобразования заданного графика получаем, что график изображается функцией вида , когда являются коэффициентами сжатия при или растяжения при вдоль и . Знак перед коэффициентами и говорит о симметричном отображении графика относительно осей, и сдвигают ее по и по .
Существует 3 вида геометрических преобразований графика:
- Масштабирование вдоль и . На это влияют коэффициенты и при условии не равности , когда , то график сжимается по , а растягивается по , когда , то график растягивается по и сжимается по .
- Симметричное отображение относительно координатных осей. При наличии знака перед симметрия идет относительно , перед идет относительно . Если отсутствует, тогда пункт при решении пропускается;
- Параллельный перенос (сдвиг) вдоль и . Преобразование производится при наличии коэффициентов и неравных . Если значение положительное, до график сдвигается влево на единиц, если отрицательное , тогда в право на такое же расстояние. Значение определяет движение по оси , что значит при положительном функция движется вверх, при отрицательном – вниз.
Степенная функция
Рассмотрим решения на примерах, начиная со степенной функции.
Преобразовать и построить график функции .
Решение
Представим функции таким образом:
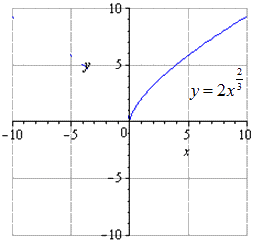
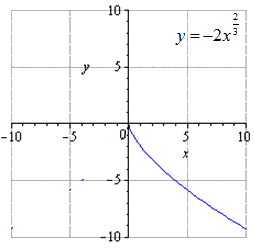
Где , стоит обратить внимание на наличие , . Отсюда получаем, что геометрические преобразования производятся с растяжения вдоль вдвое, отображается симметрично относительно , сдвигается вправо на и вверх на единицы.
Ответ: Если изобразить исходную степенную функцию, получим, что
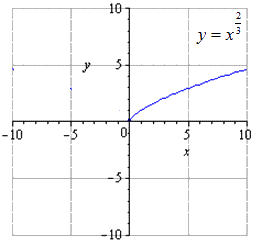
при растягивании вдвое вдоль имеем, что
Отображение, симметричное относительно , имеет вид
а движение вправо на
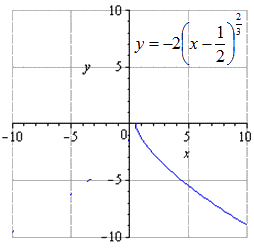
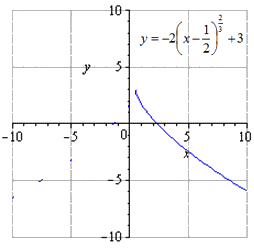
движение на единицы вверх имеет вид
Показательная функция
Преобразования показательной функции рассмотрим на примерах.
Произвести построение графика показательной функции .
Решение.
Преобразуем функцию, исходя из свойств степенной функции. Тогда получим, что
Отсюда видно, что получим цепочку преобразований :
Ответ: Получаем, что исходная показательная функция имеет вид
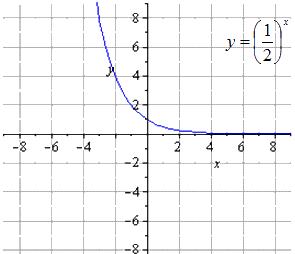
Сжимание вдвое вдоль дает
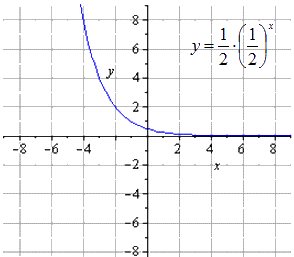
Растягивание вдоль
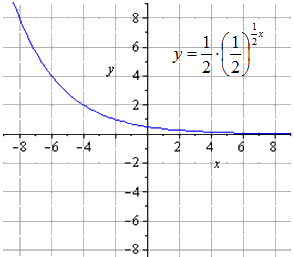
Симметричное отображение относительно
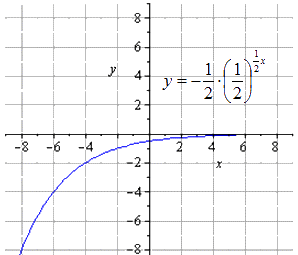
Отображение симметрично относительно
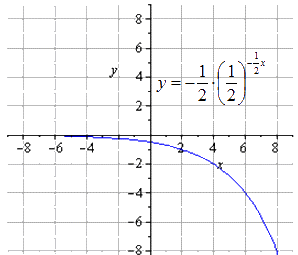
Сдвигание на единиц вверх
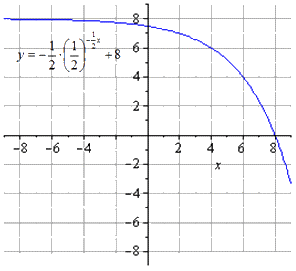
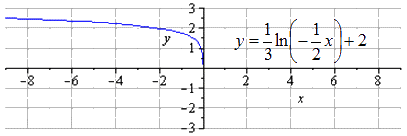
Логарифмическая функция
Рассмотрим решение на примере логарифмической функции .
Построить функцию при помощи преобразования .
Решение
Для решения необходимо использовать свойства логарифма, тогда получаем:
Преобразования логарифмической функции выглядят так:
Ответ: Изобразим график исходной логарифмической функции
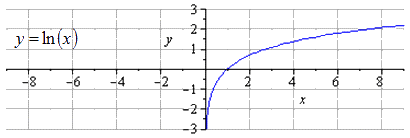
Производим сжимание строе по
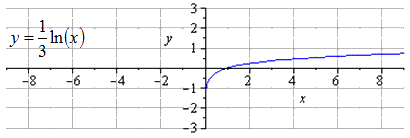
Производим растягивание вдоль
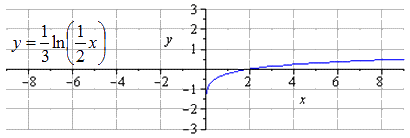
Производим отображение относительно
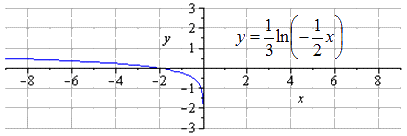
Производим сдвигание вверх на единицы, получаем
Для преобразования графиков тригонометрической функции необходимо подгонять под схему решения вида . Необходимо , чтобы приравнивался к . Отсюда получаем, что дает понять, что график функции увеличивает период по , при уменьшает его. От коэффициента зависит амплитуда колебаний синусоиды и косинусоиды.
Преобразования y = sin x
Рассмотрим примеры решения заданий с преобразованиями .
Построить график с помощью преобразований функции y=sinx.
Решение
Необходимо привести функцию к виду . Для этого:
Видно, что . Так как перед имеется , а перед - нет, тогда получим цепочку преобразований вида:
Подробное преобразование синусоиды. При построении графика исходной синусоиды получаем, что наименьшим положительным периодом считается . Нахождение максимума в точках , а минимума - .

Производится растягивание по втрое, значит возрастание амплитуды колебаний возрастет в раза. - это наименьший положительный период. Максимумы переходят в , минимумы - .
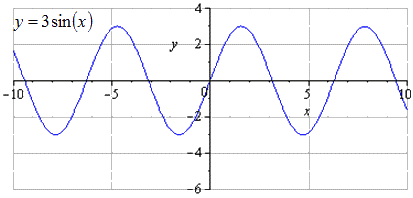
При растягивании по вдвое получаем, что наименьший положительный период увеличивается в раза и равняется . Максимумы переходят в , минимумы – в .
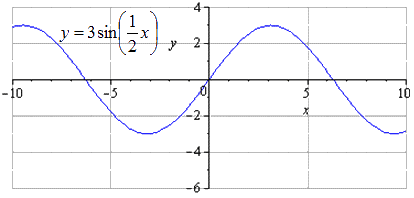
Изображение производится симметрично относительно . Наименьший положительный период в данном случае не меняется и равняется . Переход максимума выглядит как , а минимума – .
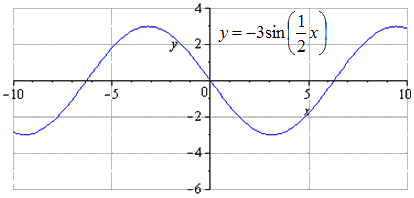
Ответ: Производится сдвижение графика вниз на единицы. Изменение наименьшего общего периода не происходит. Нахождение максимумов с перехождением в точки , минимумов - .
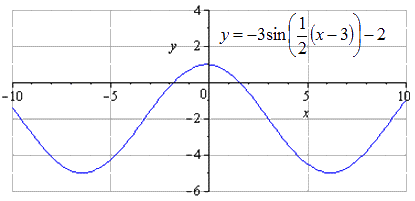
На данном этапе график тригонометрической функции считается преобразованным.
Преобразование функции y = cos x
Рассмотрим подробное преобразование функции .
Построить график функции при помощи преобразования функции вида .
Решение
По алгоритму необходимо заданную функцию привести к виду . Тогда получаем, что
Из условия видно, что , где имеет , а перед он отсутствует.
Отсюда получаем, что получится график тригонометрической функции вида:
Пошаговое преобразование косинусоиды с графической иллюстрацией.
При заданной графике видно, что наименьший общий период равняется . Нахождение максимумов в , а минимумов .
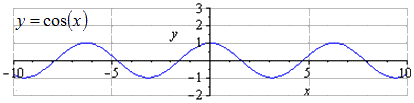
При растягивании вдоль в раза происходит возрастание амплитуды колебаний в раза. является наименьшим положительным периодом. Нахождение максимумов в , минимумов в .
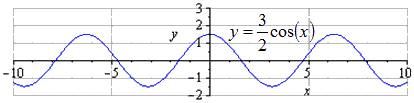
При сжатии вдоль вдвое получаем, что наименьшим положительным периодом является число . Производится переход максимумов в ,минимумов - .
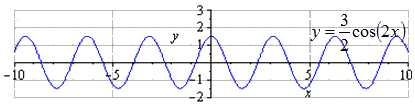
Симметричное отображение относительно . Так как график нечетный, то он не будет изменяться.
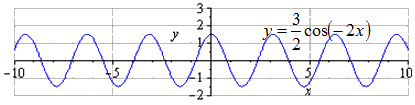
При сдвигании графика на . Отсутствуют изменения наименьшего положительного периода . Нахождение максимумов в , минимумов - .
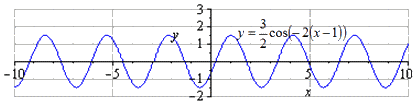
Ответ: При сдвигании на наименьший положительный период равняется и не изменен. Нахождение максимумов в , минимумов в .
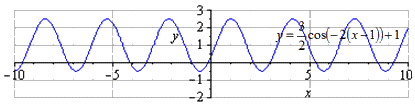
Преобразования функции косинуса завершено.
Преобразования y = tgx
Рассмотрим преобразования на примере .
Построить график функции при помощи преобразований функции .
Решение
Для начала необходимо привести заданную функцию к виду , после чего получаем, что
Отчетливо видно, что , а перед коэффициентами и имеется . Значит, после преобразования тангенсоиды получаем
Поэтапное преобразование тангенсоиды с графическим изображением.
Имеем, что исходный график – это . Изменение положительного периода равняется . Областью определения считается .
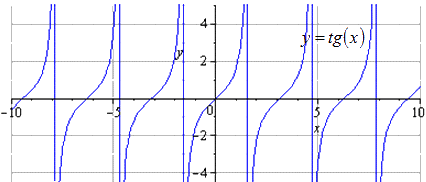
Сжимаем в раза вдоль . считается наименьшим положительным периодом, где область определения имеет вид .
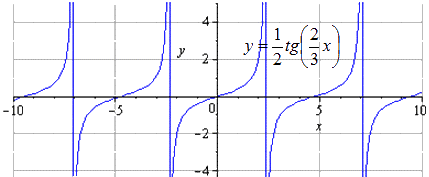
Растягиваем вдоль в раза. Вычислим наименьший положительный период, причем равнялся . А область определения функции с координатами , меняется только область определения.
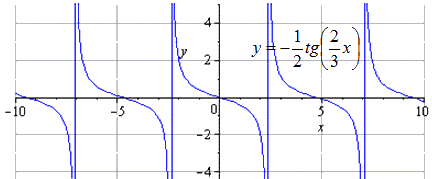
Симметрия идет по сторону . Период не изменится в этот момент.
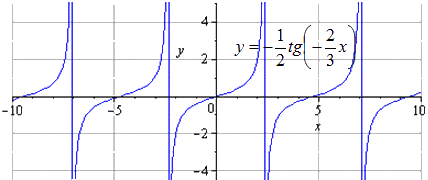
Необходимо симметрично отображать оси координат. Область определения в данном случае неизменна. График совпадает с предыдущим. Это говорит о том, что функция тангенса нечетная. Если к нечетной функции задать симметричное отображение и , тогда преобразуем до исходной функции.
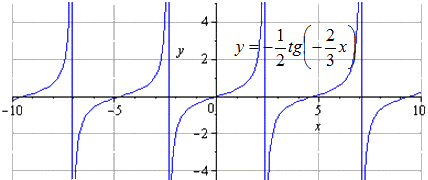
При движении вправо на видим, что наименьшим положительным периодом является . А изменения происходят внутри области определения .
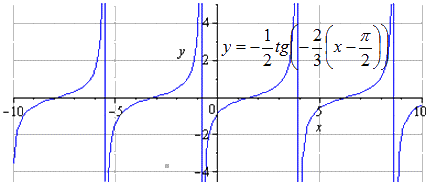
Ответ: При сдвигании графика на получаем, что изменение области определения отсутствует.
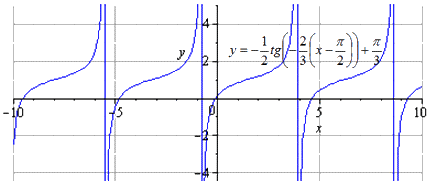
Преобразование тангенса завершено.
Тригонометрическая функция вида
Рассмотрим на примере тригонометрической функции вида .
Построить график функции при помощи преобразования .
Решение
Для начала необходимо перейти от арккосинуса к арксинусу при помощи обратных тригонометрических функций . Значит, получим, что .
Видно, что .
Поэтапное преобразование арккосинуса и графическое изображение.
График, данный по условию
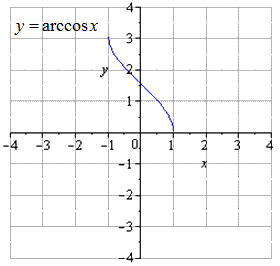
Производим отображение относительно
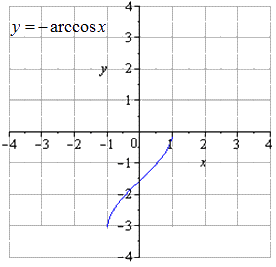
Производим движение вверх на .
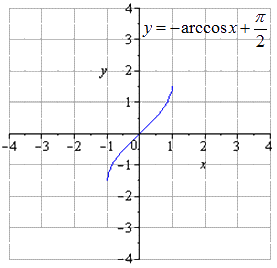
Таким образом, осуществляется переход от арккосинуса к косинусу. Необходимо произвести геометрические преобразования арксинуса и его графика.
Видно, что , где отсутствует знак у и .
Отсюда получаем, что преобразования примет вид:
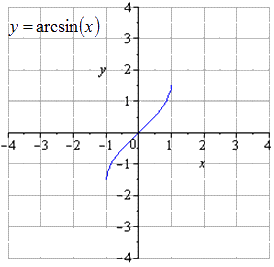
Поэтапное преобразование графика арксинуса и графическое изображение.
График имеет область определения вида , тогда интервал относится к области значений.
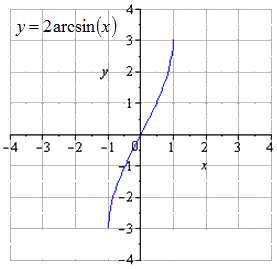
Необходимо растянуть вдвое по , причем область определения останется неизменной , а область значений .
Растягивание по строе. Происходит расширение области определения , но область значений остается неизменной .
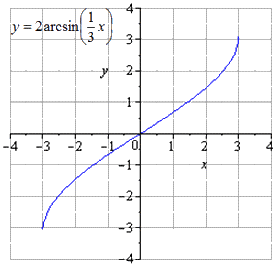
Ответ: Производим сдвигание вправо на , причем область определения становится равной . Без изменений остается область значений .
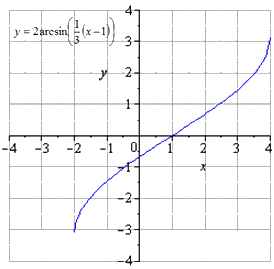
Задача преобразования графика обратной тригонометрической функции завершена. Если по условию имеются сложные функции, тогда необходимо прибегнуть к полному исследованию функция.
Математические онлайн-калькуляторы




