- 16 июля 2025
- 8 минут
- 6 177
Геометрический смысл определенного интеграла
Статью подготовили специалисты образовательного сервиса Zaochnik.
Вычисление площади является основным в теории площадей. Возникает вопрос о ее нахождении, когда фигура имеет неправильную форму или необходимо прибегнуть к ее вычислению через интеграл.
Данная статья рассказывает о вычислении площади криволинейной трапеции по геометрическому смыслу. Это позволяет выявлять связь между интегралом и площадью криволинейной трапеции. Если дана функция , причем непрерывная на интервале , знак перед выражением не меняется.
Криволинейная трапеция
Фигура, обозначенная как , ограничена линиями вида и , называется криволинейной трапецией. Она принимает обозначение .
Рассмотрим на рисунке, приведенном ниже.
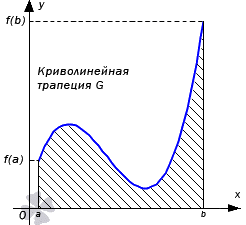
Для вычисления криволинейно трапеции необходимо разбить отрезок на количество частей с точками, определенными на , причем дать обозначение с точками . Необходимо выбрать так, чтобы при , тогда фигуры, которые соответствуют нижней и верхней частям Дарбу, считаются входящей и объемлющей многоугольными фигурами для . Рассмотрим рисунок, приведенный ниже.
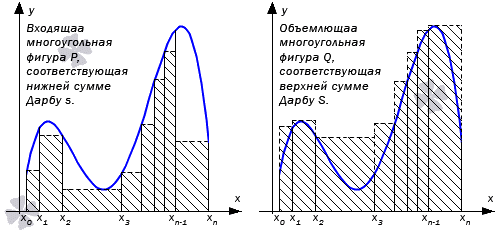
Отсюда имеем, что , причем при увеличении количества точек разбиения , получим неравенство вида , где является малым положительным числом, и являются верхними и нижними суммами Дабру из отрезка . Иначе это запишется как . Значит, при обращении к понятию определенного интеграла Дарбу, получим, что .
Из последнего равенства получим, что определенный интеграл вида является площадью криволинейной трапеции для заданной непрерывной функции вида . Это и есть геометрический смысл определенного интеграла.
При вычислении получим площадь искомой фигуры, которая ограничивается линиями и .
Замечание: Когда функция является неположительной из отрезка , тогда получаем, что площадь криволинейной трапеции вычисляется, исходя из формулы .
Вычислить площадь фигуры, которая ограничена заданными линиями вида .
Решение
Для того, чтобы решить, необходимо для начал построить фигуру на плоскости, где имеется прямая , совпадающая с , с прямыми вида и , параллельными оси , где кривая строится при помощи геометрических преобразований графика функции . Построим график.

Отсюда видно, что необходимо найти площадь криволинейной трапеции. Вспоминая геометрический смысл интеграла, получаем, что искомая площадь и будет выражена определенным интегралом, который необходимо разрешить. Значит, необходимо применить формулу . Такой неопределенный интеграл вычисляется, исходя из формулы Ньютона-Лейбница
Ответ:
Замечание: Для нахождения площади криволинейной трапеции не всегда можно построить фигуру. Тогда решение выполняется следующим образом. При известной функции неотрицательной или неположительной на отрезке , применяется формула вида или .
Произвести вычисление площади, ограниченной линиями вида .
Решение
Для построения этой фигуры получим, что совпадает с , а и являются параллельными . График функции - это парабола с координатами точки , являющейся ее вершиной с направленными вверх ветвями. Чтобы найти точки пересечения параболы с , необходимо вычислить:
Значит, парабола пересекает ох в точках и . Отсюда получим, что фигура, обозначенная как , получит вид, изображенный на рисунке ниже.

Данная фигура не является криволинейной трапецией, потому как функция вида изменяет знак на промежутке . Фигура может быть представлена в виде объединений двух криволинейных трапеций , исходя из свойства аддитивности площади, имеем, что . Рассмотрим график, приведенный ниже.

Отрезок считается неотрицательной областью параболы, тогда отсюда получаем, что площадь будет иметь вид . Отрезок неположительный для функции вида , значит, исходя из геометрического смысла определенного интеграла, получим, что . Необходимо произвести вычисления по формуле Ньютона-Лейбница. Тогда определенный интеграл примет вид:
Стоит отметить, что нахождение площади не верно по принципу
Так как полученное число является отрицательным и представляет собой разность .
Ответ:
Если фигуры ограничены линиями вида и , а функция равна , причем непрерывна и имеет неменяющийся знак на промежутке , то их называют криволинейными тарпециями. Рассмотрим на рисунке, приведенном ниже.
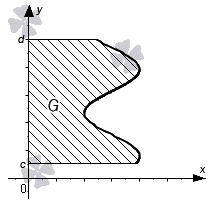
Геометрический смысл определенного интеграла
Геометрический смысл определенного интеграла заключается в том, что его значением является площадь криволинейной трапеции для непрерывной и неотрицательной функции вида , расположенной на интервале .
Справедливо считать, что имеет место быть для непрерывной и неположительной функции , расположенном на отрезке .
Произвести вычисление фигуры, которая ограничена осью ординат и линиями .
Решение
Построение графика не является простым. Поэтому необходимо решить без чертежа. Вспомним, что функция определена для всех положительных значений . Рассмотрим значения функции, имеющиеся на отрезке . По свойствам элементарных функций знаем, что логарифмическая функция возрастает на всей области определения. Тогда не отрезке является неотрицательной. Значит имеем, что . Имеющееся выражение , определенное на том же отрезке, неотрицательно. Можно сделать вывод, что функция является положительной на интервале, равном . Получаем, что фигура на этом интервале является положительной. Тогда ее площадь должна вычисляться по формуле .
Необходимо произвести вычисление неопределенного интеграла. Для этого необходимо найти первообразную функции и применить формулу Ньютона-Лейбница. Получаем, что
Рассмотрим чертеж, приведенный ниже.
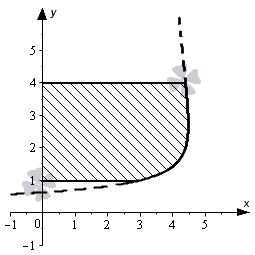
Ответ:
Итоги
В данной статье мы выявили геометрический смысл определенного интеграла и изучили связь с площадью криволинейной трапеции. Отсюда следует, что мы имеем возможность вычислять площадь сложных фигур при помощи вычисления интеграла для криволинейной трапеции. В разделе нахождения площадей и фигур, которые ограниченными линиями , данные примеры рассмотрены подробно.
Математические онлайн-калькуляторы




