Площадь фигуры: понятие площади, свойства площади, квадрируемые фигуры

Статья рассказывает о понятии площадей и их свойств. Заключительная часть статьи включит себя математическое описание квадрируемых фигур с приведением примеров решения.

Понятие площади, свойства площади

Для вычисления площади основываются на свойствах площадей:

Определение 1

положительность;
аддитивность, это когда замкнутая область представлена несколькими фигурами, которые не имеют общих точек и равняются сумме площадей этих фигур.
инвариантность;
нормированность.

Единица измерения площади – это элементарный квадрат, имеющий сторону $r$ $r$ .

Если рассмотреть фигуру $G$ $G$ с ограничениями и за обозначение площади принять $S (G)$ $S (G)$ , то при построении прямых, изобразить параллельными осям $О х$ $О х$ и $О у$ $О у$ , причем на расстоянии, равном rобозначению $r$ $r$ . Заданные прямые преобразуют сетку, которая разбивает $х О у$ $х О у$ на квадраты. Буквой $М$ $М$ обозначается фигура, которая состоящая из элементарных квадратов, которые располагаются внутри $G$ $G$ , причем не касаются границ, а $М'$ $М'$ – фигуру, которая состоит из квадратов и имеющая с границей $G$ $G$ хотя бы одну общую точку, а $М М'$ $М М'$ фигуру, которая объединяет $М$ $М$ и $М'$ $М'$ (на рисунке изображается синей и красной областями).

Площади фигур возьмем за обозначение $М$ $М$ и $М М'$ $М М'$ , значит $S (M)$ $S (M)$ и $S (M M')$ $S (M M')$ будут равны, исходя из количества составляющих квадратов. Рассмотрим рисунок, изображенный ниже.

Понятие площади, свойства площади

Если постоянно уменьшать одну из сторон квадрата, то можно получить сетку с множеством значений площадей $open S (M)}$ $openS (M)\}$ и $open S (M M)'}$ $openS (M M)'\}$ . Рассмотрим на рисунке, приведенном ниже.

Понятие площади, свойства площади

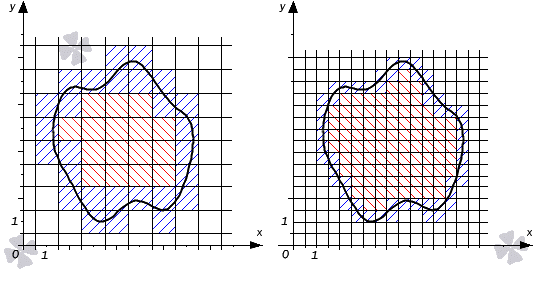
Множество $open S (M)}$ $openS (M)\}$ имеет ограничения, значит, имеет тонкую грань в виде $a = s u p open S (M)}$ $a = s u p openS (M)\}$ , тогда внутреннюю площадь обозначим как $G$ $G$ . Множество $open S (M M')}$ $openS (M M')\}$ имеет ограничения снизу, значит, нижняя грань обозначается как $A = i n f open S (M M')}$ $A = i n f openS (M M')\}$ , внешнюю площадь обозначим как $G$ $G$ .

Фигура $G$ $G$ с внешней площадью равной внутренней называют квадрируемой, а число $S (G) = a = A$ $S (G) = a = A$ является площадью этой фигуры. $S (G) = a = A$ $S (G) = a = A$ значит, что площадь квадрируемой функции является числом единственным и обладает этим свойством.

Определение 2

Площадь фигуры $G$ $G$ называется предел последовательности значений $open S (M')}$ $openS (M')\}$ , когда $r \to 0$ $r \to 0$ . Квадрируемая фигура $G$ $G$ имеет площадь равную $0$ $0$ .

Квадрируемость можно ввести иным образом, то есть рассмотреть вписанные и описанные окружности, через которые произвести вычисления.

Определение 3

Фигура $G$ $G$ считается квадрируемой, когда для любого положительного числа $open S (M')}$ $openS (M')\}$ имеется входящая и включающая многоугольные фигуры $P$ $P$ и $Q$ $Q$ , отсюда следует, что $P \subset G \subset Q$ $P \subset G \subset Q$ и $S (Q) - S (P) < ε$ $S (Q) - S (P) < ε$ .

Для примера подходит круг с вписанным и описанным $2^{n + 1}$ $2^{n + 1}$ треугольниками, где $n$ $n$ n является натуральным числом.

Квадрируемые фигуры

Рассмотрим, как необходимо изображать и задавать квадрируемые фигуры. Все встречающиеся фигуры в разделах геометрии называют квадрируемыми. Любая такая фигура имеет ограничения, то есть будем находить площади ограниченных фигур. Объединение и пересечение или разность также является квадрируемой фигурой.

Самыми распространенными видами для вычисления площадей считаются:

Если фигура квадрируема, тогда она имеет ограничения линиями графиков $y = f (x)$ $y = f (x)$ и $x = g (y)$ $x = g (y)$ . Первый рисунок, приведенный ниже, ограничивается сверху параболой $y = - \frac{1}{8} (x - 4)^{2} + 9$ $y = - \frac{1}{8} (x - 4)^{2} + 9$ , а снизу кривой вида $y = \frac{1}{3} x \cdot sin x + 2$ $y = \frac{1}{3} x \cdot \sin x + 2$ , справа и слева прямыми, имеющими значения $х = 1, х = 9$ $х = 1, х = 9$ . Второй рисунок имеет границы в виде линий $y = \frac{1}{3} (x - 6)^{2} + 1, y = ln (x - 1) + 7, y = - e^{x - 8} + 8, y = - \frac{1}{3} x + 5$ $y = \frac{1}{3} (x - 6)^{2} + 1, y = \ln (x - 1) + 7, y = - e^{x - 8} + 8, y = - \frac{1}{3} x + 5$ . Рассмотрим рисунок, приведенный ниже.

Квадрируемые фигуры

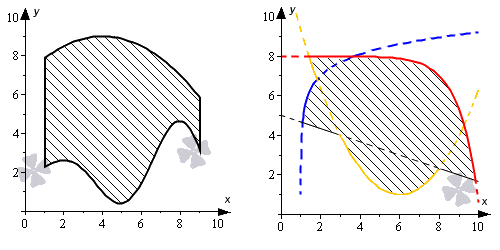
Фигура считается квадрируемой, если имеется возможность ограничения гладкими кривыми, то есть границы задаются при помощи параметрического уравнения вида $open\begin{array}{l} x = ϕ (t) \\ y = ψ (t) \end{array}$ , где функции $ϕ (t)$ и $ψ (t)$ являются непрерывными на интервале $opent_{1}; t_{2}]$ , не имеют пересечений и соответствуют условию $open\begin{array}{l} ϕ' (t_{0}) \neq 0 \\ ψ' (t_{0}) \neq 0 \end{array}$ при любом значении $t_{0} \in opent_{1}; t_{2}]$ . Для примера рассмотрим фигуру, которая ограничивается осями координат и частью астроиды вида $open\begin{array}{l} x = 3 \cos^{3} t \\ y = 3 \sin^{3} t \end{array}$ , где $t \in open0; \frac{π}{2}]$ .

Квадрируемые фигуры

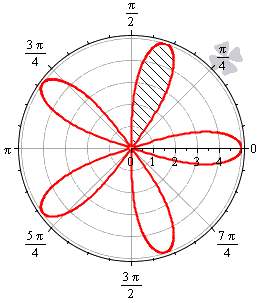
Фигура считается квадрируемой, когда она ограничена замкнутыми кривыми, где начала и конец совпадают. Явным примером такой функции является лепесток фигуры, имеющий уравнение $r = 5 \sqrt{\cos (5 φ)}$ . Рассмотрим на рисунке, приведенном ниже.

Квадрируемые фигуры

Итоги

Площадь – это такая функция, благодаря которой она определена как класс квадрируемых фигур со свойствами аддитивности, инвариантности и нормированности.