Квадратные неравенства, примеры, решения

7 ноября 2023
5 минут
4 231

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

В данном разделе мы собрали информацию о квадратных неравенствах и основных подходах к их решению. Закрепим материал разбором примеров.

Что представляет собой квадратное неравенство

Давайте посмотрим, как по виду записи различать неравенства различных видов и выделять среди них квадратные.

Определение 1

Квадратное неравенство – это такое неравенство, которое имеет вид $a \cdot x^{2} + b \cdot x + c < 0$ , где $a, b$ и $c$ – некоторые числа, причем $a$ не равно нулю. $x$ – это переменная, а на месте знака $<$ может стоять любой другой знак неравенства.

Вторым названием квадратных уравнений является название «неравенства второй степени». Объяснить наличие второго названия можно следующим образом. В левой части неравенства находится многочлен второй степени – квадратный трехчлен. Применение к квадратным неравенствам термина «квадратичные неравенства» некорректен, так как квадратичными являются функции, которые задаются уравнениями вида $y = a \cdot x^{2} + b \cdot x + c$ .

Приведем пример квадратного неравенства:

Пример 1

Возьмем $5 \cdot x^{2} - 3 \cdot x + 1 > 0$ . В этом случае $a = 5, b = - 3$ и $c = 1$ .

Или вот такое неравенство:

Пример 2

$- 2, 2 \cdot z^{2} - 0, 5 \cdot z - 11 \leq 0$ , где $a = - 2, 2, b = - 0, 5$ и $c = - 11$ .

Покажем несколько примеров квадратных неравенств:

Пример 3

Здесь коэффициенты этого квадратного неравенства есть ; $1 \frac{2}{3} \cdot x^{2} - x + \frac{5}{7} < 0$ , в этом случае $a = 1 \frac{2}{3}, b = - 1, c = \frac{5}{7}$ .

Особое внимание нужно обратить на тот факт, что коэффициент при $x^{2}$ считается неравным нулю. Объясняется это тем, что иначе мы получим линейное неравенство вида $b \cdot x + c > 0$ , так как квадратная переменная при умножении на ноль сама станет равной нулю. При этом, коэффициенты $b$ и c могут быть равны нулю как вместе, так и по отдельности.

Пример 4

Пример такого неравенства $x^{2} - 5 \geq 0$ .

Способы решения квадратных неравенств

Основным метода три:

Определение 2

графический;
метод интервалов;
через выделение квадрата двучлена в левой части.

Графический метод

Метод предполагает проведение построения и анализа графика квадратичной функции $y = a \cdot x^{2} + b \cdot x + c$ для квадратных неравенств $a \cdot x^{2} + b \cdot x + c < 0 (\leq, >, \geq)$ . Решением квадратного неравенства являются промежутки или интервалы, на которых указанная функция принимает положительные и отрицательные значения.

Метод интервалов

Решить квадратное неравенство с одной переменной можно методом интервалов. Метод применим для решения любого вида неравенств, не только квадратных. Суть метода в том, чтобы определить знаки промежутков, на которые разбивается ось координат нулями трехчлена $a \cdot x^{2} + b \cdot x + c$ при их наличии.

Для неравенства $a \cdot x^{2} + b \cdot x + c < 0$ решениями являются промежутки со знаком минус, для неравенства $a \cdot x^{2} + b \cdot x + c > 0$ , промежутки со знаком плюс. Если мы имеем дело с нестрогими неравенствами, то решением становится интервал, который включает точки, которые соответствуют нулям трехчлена.

Выделение квадрата двучлена

Принцип выделения квадрата двучлена в левой части квадратного неравенства состоит в выполнении равносильных преобразований, которые позволяют перейти к решению равносильного неравенства вида $(x - p)^{2} < q (\leq, >, \geq)$ , где $p$ и $q$ – некоторые числа.

Неравенства, сводящиеся к квадратным

К квадратным неравенствам с помощью равносильных преобразований можно прийти от неравенств других видов. Сделать это можно разными способами. Например, перестановкой в данном неравенства слагаемых или переносом слагаемых из одной части в другую.

Приведем пример. Рассмотрим равносильное преобразование неравенства $5 \leq 2 \cdot x - 3 \cdot x^{2}$ . Если мы перенесем все слагаемые из правой части в левую, то получим квадратное неравенство вида $3 \cdot x^{2} - 2 \cdot x + 5 \leq 0$ .

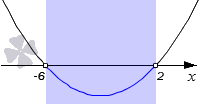
Неравенства, сводящиеся к квадратным — Пример 5

Примером неравенств, которые часто сводятся к квадратным, могут служить иррациональные и логарифмические неравенства. Так, например, неравенство $\sqrt{2 \cdot x^{2} + 5} < \sqrt{x^{2} + 6 \cdot x + 14}$

равносильно квадратному неравенству $x^{2} - 6 \cdot x - 9 < 0$ , а логарифмическое неравенство $\log_{3} (x^{2} + x + 7) \geq 2$ – неравенству $x^{2} + x - 2 \geq 0$ .