- 16 июля 2025
- 8 минут
- 5 733
Решение квадратных неравенств методом интервалов
Статью подготовили специалисты образовательного сервиса Zaochnik.
Универсальным методом решения неравенств по праву считается метод интервалов. Именно его проще всего использовать для решения квадратных неравенств с одной переменной. В этом материале мы рассмотрим все аспекты применения метода интервалов для решения квадратных неравенств. Для облегчения усвоения материала мы рассмотрим большое количество примеров разной степени сложности.
Алгоритм применения метода интервалов
Рассмотрим алгоритм применения метода интервалов в адаптированном варианте, который пригоден для решения квадратных неравенств. Именно с таким вариантом метода интервалов знакомят учеников на уроках алгебры. Не будем усложнять задачу и мы.
Перейдем собственно к алгоритму.
У нас есть квадратный трехчлен из левой части квадратного неравенства. Находим нули из этого трехчлена.
В системе координат изображаем координатную прямую. Отмечаем на ней корни. Для удобства можем ввести разные способы обозначения точек для строгих и нестрогих неравенств. Давайте договоримся, что «пустыми» точками мы будем отмечать координаты при решении строгого неравенства, а обычными точками - нестрогого. Отметив точки, мы получаем на координатной оси несколько промежутков.
Если на первом шаге мы нашли нули, то определяем знаки значений трехчлена для каждого из полученных промежутков. Если нули мы не получили, то производим это действие для всей числовой прямой. Отмечаем промежутки знаками «» или «».
Дополнительно мы будем вводить штриховку в тех случаях, когда будем решать неравенства со знаками или и или . В первом случае штриховка будет наноситься над промежутками, отмеченными «», во втором над участками, отмеченными «».
Отметив знаки значений трехчлена и нанеся штриховку над отрезками, мы получаем геометрический образ некоторого числового множества, которое фактически является решением неравенства. Нам остается лишь записать ответ.
Остановимся подробнее на третьем шаге алгоритма, который предполагает определение знака промежутка. Существует несколько подходов определения знаков. Рассмотрим их по порядку, начав с наиболее точного, хотя и не самого быстрого. Этот метод предполагает вычисление значений трехчлена в нескольких точках полученных промежутков.
Для примера возьмем трехчлен .
Корни этого трехчлена и разбивают координатную ось на три промежутка , и .
Начнем с промежутка . Для того, чтобы упростить себе задачу, примем . Получаем .
– положительное число. Это значит, что значения данного квадратного трехчлена на интервале положительные и его можно обозначить знаком «».
Для определения знака промежутка примем . Имеем . Ставим над интервалом знак «».
Для промежутка возьмем , получаем . Отмечаем этот интервал знаком «».
Намного быстрее определить знаки можно с учетом следующих фактов.
При положительном дискриминанте квадратный трехчлен с двумя корнями дает чередование знаков его значений на промежутках, на которые разбивается числовая ось корнями этого трехчлена. Это значит, что нам вовсе не обязательно определять знаки для каждого из интервалов. Достаточно провести вычисления для одного и проставить знаки для остальных, учитывая принцип чередования.
При желании, можно и вовсе обойтись без вычислений, сделав выводы о знаках по значению старшего коэффициента. Если , то мы получаем последовательность знаков , а если – то .
У квадратных трехчленов с одним корнем, когда дискриминант равен нулю, мы получаем два промежутка на координатной оси с одинаковыми знаками. Это значит, что мы определяем знак для одного из промежутков и для второго ставим такой же.
Здесь также применим метод определения знака на основе значения коэффициента : если , то будет , а если , то.
Если квадратный трехчлен не имеет корней, то знаки его значений для всей координатной прямой совпадают как со знаком старшего коэффициента , так и со знаком свободного члена .
Например, если мы возьмем квадратный трехчлен , он не имеет корней (его дискриминант отрицательный). Коэффициент при есть отрицательное число , и свободный член тоже отрицателен. Это значит, что на промежутке его значения отрицательны.
Примеры решения квадратных неравенств
Рассмотрим примеры решения квадратных неравенств с использованием рассмотренного выше алгоритма.
Решите неравенство .
Решение
Используем для решения неравенства метод интервалов. Для этого найдем корни квадратного трехчлена . В связи с тем, что коэффициент при х четный, нам будет удобнее вычислить не дискриминант, а четвертую часть дискриминанта: .
Дискриминант больше нуля. Это позволяет нам найти два корня квадратного трехчлена: и . Отметим эти значения на числовой прямой. Так как уравнение нестрогое, то на графике мы используем обычные точки.
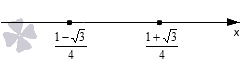
Теперь по методу интервалов определяем знаки трех полученных интервалов. Коэффициент при равен , то есть, положителен, следовательно, последовательность знаков будет .
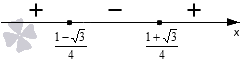
Так как мы решаем неравенство со знаком , то изображаем штриховку над промежутками со знаками плюс:
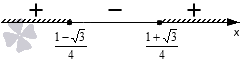
Запишем аналитически числовое множество по полученному графическому изображению. Мы можем сделать это двумя способами:
или .
Ответ: или .
Выполните решение квадратного неравенства методом интервалов.
Решение
Для начала найдем корни квадратного трехчлена из левой части неравенства:
Это строгое неравенство, поэтому на графике используем «пустую» точку. С координатой .
Теперь нам нужно определить знаки на полученных промежутках и . Так как дискриминант квадратного трехчлена равен нулю, а старший коэффициент отрицательный, то мы проставляем знаки :
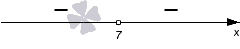
Так как мы решаем неравенство со знаком , то изображаем штриховку над интервалами со знаками минус:
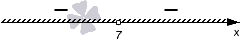
В данном случае решениями являются оба промежутка .
Ответ: или в другой записи .
Имеет ли квадратное неравенство решения?
Решение
Найдем корни квадратного трехчлена из левой части неравенства. Для этого найдем дискриминант: . Дискриминант меньше нуля, значит, действительных корней нет.
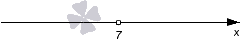
Графическое изображение будет иметь вид числовой прямой без отмеченных на ней точек.

Определим знак значений квадратного трехчлена. При он совпадает со знаком коэффициента при , то есть, со знаком числа , оно положительное, следовательно, имеем знак :
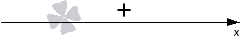
Штриховку мы могли бы нанести в данном случае над промежутками со знаком «». Но таких промежутков у нас нет. Следовательно, чертеж сохраняет вот такой вид:
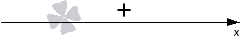
В результате вычислений мы получили пустое множество. Это значит, что данное квадратное неравенство решений не имеет.
Ответ: Нет.
Математические онлайн-калькуляторы




