Метод наименьших квадратов

Содержание:

16 апреля 2024
8 минут
5279

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Начнем статью сразу с примера. У нас есть некие экспериментальные данные о значениях двух переменных – $x$ и $y$ . Занесем их в таблицу.

	$i = 1$	$i = 2$	$i = 3$	$i = 4$	$i = 5$
$x_{i}$	$0$	$1$	$2$	$4$	$5$
$y_{i}$	$2, 1$	$2, 4$	$2, 6$	$2, 8$	$3, 0$

После выравнивания получим функцию следующего вида: $g (x) = \sqrt[3]{x + 1} + 1$ .

Мы можем аппроксимировать эти данные с помощью линейной зависимости $y = a x + b$ , вычислив соответствующие параметры. Для этого нам нужно будет применить так называемый метод наименьших квадратов. Также потребуется сделать чертеж, чтобы проверить, какая линия будет лучше выравнивать экспериментальные данные.

В чем именно заключается МНК (метод наименьших квадратов)

Главное, что нам нужно сделать, – это найти такие коэффициенты линейной зависимости, при которых значение функции двух переменных $F (a, b) = \sum_{i = 1}^{n} (y_{i} - (a x_{i} + b))^{2}$ будет наименьшим. Иначе говоря, при определенных значениях $a$ и $b$ сумма квадратов отклонений представленных данных от получившейся прямой будет иметь минимальное значение. В этом и состоит смысл метода наименьших квадратов. Все, что нам надо сделать для решения примера – это найти экстремум функции двух переменных.

Как вывести формулы для вычисления коэффициентов

Для того чтобы вывести формулы для вычисления коэффициентов, нужно составить и решить систему уравнений с двумя переменными. Для этого мы вычисляем частные производные выражения $F (a, b) = \sum_{i = 1}^{n} (y_{i} - (a x_{i} + b))^{2}$ по $a$ и $b$ и приравниваем их к $0$ .

$\{\begin{cases} \frac{δ F (a, b)}{δ a} = 0 \\ \frac{δ F (a, b)}{δ b} = 0 \end{cases} \Leftrightarrow \{\begin{cases} - 2 \sum_{i = 1}^{n} (y_{i} - (a x_{i} + b)) x_{i} = 0 \\ - 2 \sum_{i = 1}^{n} (y_{i} - (a x_{i} + b)) = 0 \end{cases} \Leftrightarrow \{\begin{cases} a \sum_{i = 1}^{n} x_{i}^{2} + b \sum_{i = 1}^{n} x_{i} = \sum_{i = 1}^{n} x_{i} y_{i} \\ a \sum_{i = 1}^{n} x_{i} + \sum_{i = 1}^{n} b = \sum_{i = 1}^{n} y_{i} \end{cases} \Leftrightarrow \{\begin{cases} a \sum_{i = 1}^{n} x_{i}^{2} + b \sum_{i = 1}^{n} x_{i} = \sum_{i = 1}^{n} x_{i} y_{i} \\ a \sum_{i = 1}^{n} x_{i} + n b = \sum_{i = 1}^{n} y_{i} \end{cases}$

Для решения системы уравнений можно использовать любые методы, например, подстановку или метод Крамера. В результате у нас должны получиться формулы, с помощью которых вычисляются коэффициенты по методу наименьших квадратов.

$\{\begin{cases} \frac{n \sum_{i = 1}^{n} x_{i} y_{i} - \sum_{i = 1}^{n} x_{i} \sum_{i = 1}^{n} y_{i}}{n \sum_{i = 1}^{n} - {(\sum_{i = 1}^{n} x_{i})}^{2}} \\ b = \frac{\sum_{i = 1}^{n} y_{i} - a \sum_{i = 1}^{n} x_{i}}{n} \end{cases}$

Мы вычислили значения переменных, при который функция
$F (a, b) = \sum_{i = 1}^{n} (y_{i} - (a x_{i} + b))^{2}$ примет минимальное значение. В третьем пункте мы докажем, почему оно является именно таким.

Это и есть применение метода наименьших квадратов на практике. Его формула, которая применяется для поиска параметра $a$ , включает в себя $\sum_{i = 1}^{n} x_{i}, \sum_{i = 1}^{n} y_{i}, \sum_{i = 1}^{n} x_{i} y_{i}, \sum_{i = 1}^{n} x_{i}^{2}$ , а также параметр
$n$ – им обозначено количество экспериментальных данных. Советуем вам вычислять каждую сумму отдельно. Значение коэффициента $b$ вычисляется сразу после $a$ .

Обратимся вновь к исходному примеру.

Пример 1

Здесь у нас $n$ равен пяти. Чтобы было удобнее вычислять нужные суммы, входящие в формулы коэффициентов, заполним таблицу.

	$i = 1$	$i = 2$	$i = 3$	$i = 4$	$i = 5$	$\sum_{i = 1}^{5}$
$x_{i}$	$0$	$1$	$2$	$4$	$5$	$12$
$y_{i}$	$2, 1$	$2, 4$	$2, 6$	$2, 8$	$3$	$12, 9$
$x_{i} y_{i}$	$0$	$2, 4$	$5, 2$	$11, 2$	$15$	$33, 8$
$x_{i}^{2}$	$0$	$1$	$4$	$16$	$25$	$46$

Решение

Четвертая строка включает в себя данные, полученные при умножении значений из второй строки на значения третьей для каждого отдельного $i$ . Пятая строка содержит данные из второй, возведенные в квадрат. В последнем столбце приводятся суммы значений отдельных строчек.

Воспользуемся методом наименьших квадратов, чтобы вычислить нужные нам коэффициенты $a$ и $b$ . Для этого подставим нужные значения из последнего столбца и подсчитаем суммы:

$\{\begin{cases} \frac{n \sum_{i = 1}^{n} x_{i} y_{i} - \sum_{i = 1}^{n} x_{i} \sum_{i = 1}^{n} y_{i}}{n \sum_{i = 1}^{n} - {(\sum_{i = 1}^{n} x_{i})}^{2}} \\ b = \frac{\sum_{i = 1}^{n} y_{i} - a \sum_{i = 1}^{n} x_{i}}{n} \end{cases} \Rightarrow \{\begin{array}{l} a = \frac{5 \cdot 33, 8 - 12 \cdot 12, 9}{5 \cdot 46 - 12^{2}} \\ b = \frac{12, 9 - a \cdot 12}{5} \end{array} \Rightarrow \{\begin{cases} a \approx 0, 165 \\ b \approx 2, 184 \end{cases}$

У нас получилось, что нужная аппроксимирующая прямая будет выглядеть как $y = 0, 165 x + 2, 184$ . Теперь нам надо определить, какая линия будет лучше аппроксимировать данные – $g (x) = \sqrt[3]{x + 1} + 1$ или $0, 165 x + 2, 184$ . Произведем оценку с помощью метода наименьших квадратов.

Чтобы вычислить погрешность, нам надо найти суммы квадратов отклонений данных от прямых $σ_{1} = \sum_{i = 1}^{n} (y_{i} - (a x_{i} + b_{i}))^{2}$ и $σ_{2} = \sum_{i = 1}^{n} (y_{i} - g (x_{i}))^{2}$ , минимальное значение будет соответствовать более подходящей линии.

$σ_{1} = \sum_{i = 1}^{n} (y_{i} - (a x_{i} + b_{i}))^{2} = = \sum_{i = 1}^{5} (y_{i} - (0, 165 x_{i} + 2, 184))^{2} \approx 0, 019 σ_{2} = \sum_{i = 1}^{n} (y_{i} - g (x_{i}))^{2} = = \sum_{i = 1}^{5} (y_{i} - (\sqrt[3]{x_{i} + 1} + 1))^{2} \approx 0, 096$

Ответ: поскольку $σ_{1} < σ_{2}$ , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
$y = 0, 165 x + 2, 184$ .

Как изобразить МНК на графике функций

Метод наименьших квадратов наглядно показан на графической иллюстрации. С помощью красной линии отмечена прямая $g (x) = \sqrt[3]{x + 1} + 1$ , синей – $y = 0, 165 x + 2, 184$ . Исходные данные обозначены розовыми точками.

Как изобразить МНК на графике функций

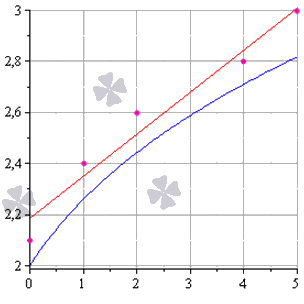
Поясним, для чего именно нужны приближения подобного вида.

Они могут быть использованы в задачах, требующих сглаживания данных, а также в тех, где данные надо интерполировать или экстраполировать. Например, в задаче, разобранной выше, можно было бы найти значение наблюдаемой величины y при $x = 3$ или при $x = 6$ . Таким примерам мы посвятили отдельную статью.

Доказательство метода МНК

Чтобы функция приняла минимальное значение при вычисленных $a$ и $b$ , нужно, чтобы в данной точке матрица квадратичной формы дифференциала функции вида $F (a, b) = \sum_{i = 1}^{n} (y_{i} - (a x_{i} + b))^{2}$ была положительно определенной. Покажем, как это должно выглядеть.

Пример 2

У нас есть дифференциал второго порядка следующего вида:

$d^{2} F (a; b) = \frac{δ^{2} F (a; b)}{δ a^{2}} d^{2} a + 2 \frac{δ^{2} F (a; b)}{δ a δ b} d a d b + \frac{δ^{2} F (a; b)}{δ b^{2}} d^{2} b$

Решение

$\frac{δ^{2} F (a; b)}{δ a^{2}} = \frac{δ (\frac{δ F (a; b)}{δ a})}{δ a} = = \frac{δ (- 2 \sum_{i = 1}^{n} (y_{i} - (a x_{i} + b)) x_{i})}{δ a} = 2 \sum_{i = 1}^{n} (x_{i})^{2} \frac{δ^{2} F (a; b)}{δ a δ b} = \frac{δ (\frac{δ F (a; b)}{δ a})}{δ b} = = \frac{δ (- 2 \sum_{i = 1}^{n} (y_{i} - (a x_{i} + b)) x_{i})}{δ b} = 2 \sum_{i = 1}^{n} x_{i} \frac{δ^{2} F (a; b)}{δ b^{2}} = \frac{δ (\frac{δ F (a; b)}{δ b})}{δ b} = \frac{δ (- 2 \sum_{i = 1}^{n} (y_{i} - (a x_{i} + b)))}{δ b} = 2 \sum_{i = 1}^{n} (1) = 2 n$

Иначе говоря, можно записать так: $d^{2} F (a; b) = (2 \sum_{i = 1}^{n} (x_{i})^{2}) d^{2} a + 2 \cdot (2 {\sum x_{i}}_{i = 1}^{n}) d a d b + (2 n) d^{2} b$ .

Мы получили матрицу квадратичной формы вида $M = (\begin{matrix} 2 \sum_{i = 1}^{n} (x_{i})^{2} & 2 \sum_{i = 1}^{n} x_{i} \\ 2 \sum_{i = 1}^{n} x_{i} & 2 n \end{matrix})$ .

В этом случае значения отдельных элементов не будут меняться в зависимости от $a$ и $b$ . Является ли эта матрица положительно определенной? Чтобы ответить на этот вопрос, проверим, являются ли ее угловые миноры положительными.

Вычисляем угловой минор первого порядка: $(2 \sum_{i = 1}^{n} (x_{i})^{2}) > 0$ . Поскольку точки $x_{i}$ не совпадают, то неравенство является строгим. Будем иметь это в виду при дальнейших расчетах.

Вычисляем угловой минор второго порядка:

$d e t (M) = |\begin{matrix} 2 \sum_{i = 1}^{n} (x_{i})^{2} & 2 \sum_{i = 1}^{n} x_{i} \\ 2 \sum_{i = 1}^{n} x_{i} & 2 n \end{matrix}| = 4 (n \sum_{i = 1}^{n} (x_{i})^{2} - {(\sum_{i = 1}^{n} x_{i})}^{2})$

После этого переходим к доказательству неравенства $(n \sum_{i = 1}^{n} (x_{i})^{2} - {(\sum_{i = 1}^{n} x_{i})}^{2}) > 0$ с помощью математической индукции.

Проверим, будет ли данное неравенство справедливым при произвольном $n$ . Возьмем $2$ и подсчитаем:

$2 \sum_{i = 1}^{2} (x_{i})^{2} - {(\sum_{i = 1}^{2} x_{i})}^{2} = 2 (x_{1}^{2} + x_{2}^{2}) - {(x_{1} + x_{2})}^{2} = = x_{1}^{2} - 2 x_{1} x_{2} + x_{2}^{2} = {(x_{1} + x_{2})}^{2} > 0$

У нас получилось верное равенство (если значения $x_{1}$ и $x_{2}$ не будут совпадать).

Сделаем предположение, что данное неравенство будет верным для $n$ , т.е. $n \sum_{i = 1}^{n} (x_{i})^{2} - {(\sum_{i = 1}^{n} x_{i})}^{2} > 0$ – справедливо.
Теперь докажем справедливость при $n + 1$ , т.е. что $(n + 1) \sum_{i = 1}^{n + 1} (x_{i})^{2} - {(\sum_{i = 1}^{n + 1} x_{i})}^{2} > 0$ , если верно $n \sum_{i = 1}^{n} (x_{i})^{2} - {(\sum_{i = 1}^{n} x_{i})}^{2} > 0$ .

Вычисляем:

$(n + 1) \sum_{i = 1}^{n + 1} (x_{i})^{2} - {(\sum_{i = 1}^{n + 1} x_{i})}^{2} = = (n + 1) (\sum_{i = 1}^{n} (x_{i})^{2} + x_{n + 1}^{2}) - {(\sum_{i = 1}^{n} x_{i} + x_{n + 1})}^{2} = = n \sum_{i = 1}^{n} (x_{i})^{2} + n \cdot x_{n + 1}^{2} + \sum_{i = 1}^{n} (x_{i})^{2} + x_{n + 1}^{2} - - ({(\sum_{i = 1}^{n} x_{i})}^{2} + 2 x_{n + 1} \sum_{i = 1}^{n} x_{i} + x_{n + 1}^{2}) = = \{\sum_{i = 1}^{n} (x_{i})^{2} - {(\sum_{i = 1}^{n} x_{i})}^{2}\} + n \cdot x_{n + 1}^{2} - x_{n + 1} \sum_{i = 1}^{n} x_{i} + \sum_{i = 1}^{n} (x_{i})^{2} = = \{\sum_{i = 1}^{n} (x_{i})^{2} - {(\sum_{i = 1}^{n} x_{i})}^{2}\} + (x_{n + 1}^{2} - 2 x_{n + 1} x_{1} + x_{1}^{2}) + + (x_{n + 1}^{2} - 2 x_{n + 1} x_{2} + x_{2}^{2}) + . . . + (x_{n + 1}^{2} - 2 x_{n + 1} x_{1} + x_{n}^{2}) = = \{n \sum_{i = 1}^{n} (x_{i})^{2} - {(\sum_{i = 1}^{n} x_{i})}^{2}\} + + (x_{n + 1} - x_{1})^{2} + (x_{n + 1} - x_{2})^{2} + . . . + (x_{n - 1} - x_{n})^{2} > 0$

Выражение, заключенное в фигурные скобки, будет больше $0$ (исходя из того, что мы предполагали в пункте $2$ ), и остальные слагаемые будут больше $0$ , поскольку все они являются квадратами чисел. Мы доказали неравенство.

Ответ: найденные $a$ и $b$ будут соответствовать наименьшему значению функции $F (a, b) = \sum_{i = 1}^{n} (y_{i} - (a x_{i} + b))^{2}$ , значит, они являются искомыми параметрами метода наименьших квадратов (МНК).