Канонические уравнения прямой в пространстве: теория, примеры, решение задач

Содержание:

06 марта 2023
16 минут
4322

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Одним из видов уравнений прямой в пространстве является каноническое уравнение. Мы рассмотрим это понятие во всех подробностях, поскольку знать его необходимо для решения многих практических задач.

В первом пункте мы сформулируем основные уравнения прямой, расположенной в трехмерном пространстве, и приведем несколько примеров. Далее покажем способы вычисления координат направляющего вектора при заданных канонических уравнениях и решение обратной задачи. В третьей части мы расскажем, как составляется уравнение прямой, проходящей через $2$ заданные точки в трехмерном пространстве, а в последнем пункте укажем на связи канонических уравнений с другими. Все рассуждения будут проиллюстрированы примерами решения задач.

Что такое каноническое уравнение прямой в пространстве

О том, что вообще из себя представляют канонические уравнения прямой, мы уже говорили в статье, посвященной уравнениям прямой на плоскости. Случай с трехмерным пространством мы разберем по аналогии.

Допустим, у нас есть прямоугольная система координат $O x y z$ , в которой задана прямая. Как мы помним, задать прямую можно разными способами. Используем самый простой из них – зададим точку, через которую будет проходить прямая, и укажем направляющий вектор. Если обозначить прямую буквой $a$ , а точку $M$ , то можно записать, что $M_{1} (x_{1}, y_{1}, z_{1})$ лежит на прямой $a$ и направляющим вектором этой прямой будет $\vec{a} = (a_{x}, a_{y}, a_{z})$ . Чтобы множество точек $M (x, y, z)$ определяло прямую $a$ , векторы $\vec{M_{1} M}$ и $\vec{a}$ должны быть коллинеарными,

Что такое каноническое уравнение прямой в пространстве

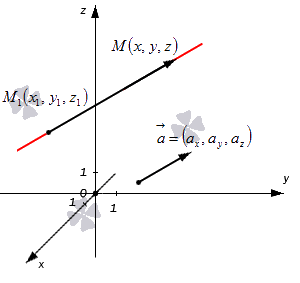
Если мы знаем координаты векторов $\vec{M_{1} M}$ и $\vec{a}$ , то можем записать в координатной форме необходимое и достаточное условие их коллинеарности. Из первоначальных условий нам уже известны координаты $\vec{a}$ . Для того чтобы получить координаты $\vec{M_{1} M}$ , нам необходимо вычислить разность между $M (x, y, z)$ и $M_{1} (x_{1}, y_{1}, z_{1})$ . Запишем:

$\vec{M_{1} M} = (x - x_{1}, y - y_{1}, z - z_{1})$

После этого нужное нам условие мы можем сформулировать так: $\vec{M_{1} M} = (x - x_{1}, y - y_{1}, z - z_{1})$ и $\vec{a} = (a_{x}, a_{y}, a_{z})$ : $\vec{M_{1} M} = λ \cdot \vec{a} \Leftrightarrow \{\begin{cases} \begin{array}{l} x - x_{1} = λ \cdot a_{x} \\ y - y_{1} = λ \cdot a_{y} \end{array} \\ z - z_{1} = λ \cdot a_{z} \end{cases}$

Здесь значением переменной $λ$ может быть любое действительное число или ноль. Если $λ = 0$ , то $M (x, y, z)$ и $M_{1} (x_{1}, y_{1}, z_{1})$ совпадут, что не противоречит нашим рассуждениям.

При значениях $a_{x} \neq 0, a_{y} \neq 0, a_{z} \neq 0$ мы можем разрешить относительно параметра $λ$ все уравнения системы $\{\begin{cases} \begin{array}{l} x - x_{1} = λ \cdot a_{x} \\ y - y_{1} = λ \cdot a_{y} \end{array} \\ z - z_{1} = λ \cdot a_{z} \end{cases}$

Между правыми частями после этого можно будет поставить знак равенства:

$\{\begin{cases} \begin{array}{l} x - x_{1} = λ \cdot a_{x} \\ y - y_{1} = λ \cdot a_{y} \end{array} \\ z - z_{1} = λ \cdot a_{z} \end{cases} \Leftrightarrow \{\begin{cases} \begin{array}{l} λ = \frac{x - x_{1}}{a_{x}} \\ λ = \frac{y - y_{1}}{a_{y}} \end{array} \\ λ = \frac{z - z_{1}}{a_{z}} \end{cases} \Leftrightarrow \frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}}$

В итоге у нас получились уравнения $\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}}$ , с помощью которых можно определить искомую прямую в трехмерном пространстве. Это и есть нужные нам канонические уравнения.

Такая запись используется даже при нулевых значениях одного или двух параметров $a_{x}, a_{y}, a_{z}$ , поскольку она в этих случаях она также будет верна. Все три параметра не могут быть равны $0$ , поскольку направляющий вектор $\vec{a} = (a_{x}, a_{y}, a_{z})$ нулевым не бывает.

Если один-два параметра $a$ равны $0$ , то уравнение $\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}}$ носит условный характер. Его следует считать равным следующей записи:

$\{\begin{cases} \begin{array}{l} x = x_{1} + a_{x} \cdot λ \\ y = y_{1} + a_{y} \cdot λ \end{array} \\ z = z_{1} + a_{z} \cdot λ \end{cases}, λ \in R$ .

Частные случаи канонических уравнений мы разберем в третьем пункте статьи.

Из определения канонического уравнения прямой в пространстве можно сделать несколько важных выводов. Рассмотрим их.

1) если исходная прямая будет проходить через две точки $M_{1} (x_{1}, y_{1}, z_{1})$ и $M_{2} (x_{2}, y_{2}, z_{2})$ , то канонические уравнения примут следующий вид:

$\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}}$ или $\frac{x - x_{2}}{a_{x}} = \frac{y - y_{2}}{a_{y}} = \frac{z - z_{2}}{a_{z}}$ .

2) поскольку $\vec{a} = (a_{x}, a_{y}, a_{z})$ является направляющим вектором исходной прямой, то таковыми будут являться и все векторы $μ \cdot \vec{a} = (μ \cdot a_{x}, μ \cdot a_{y}, μ \cdot a_{z}), μ \in R, μ \neq 0$ . Тогда прямая может быть определена с помощью уравнения $\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}}$ или $\frac{x - x_{1}}{μ \cdot a_{x}} = \frac{y - y_{1}}{μ \cdot a_{y}} = \frac{z - z_{1}}{μ \cdot a_{z}}$ .

Вот несколько примеров таких уравнений с заданными значениями:

Пример 1

$\frac{x - \sqrt{3}}{2} = \frac{y + 1}{- \frac{1}{2}} = \frac{z}{\ln 7}$

Тут $x_{1} = \sqrt{3}, y_{1} = - 1, z_{1} = 0, a_{x} = 2, a_{y} = - \frac{1}{2}, a_{z} = \ln 7$ .

Пример 2

$\frac{x - 4}{0} = \frac{y + 2}{1} = \frac{z + 1}{0}$

Тут $M_{1} (4, - 2, - 1), \vec{a} = (0, 1, 0)$ .

Как составить каноническое уравнение прямой в пространстве

Мы выяснили, что канонические уравнения вида $\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}}$ будут соответствовать прямой, проходящей через точку $M_{1} (x_{1}, y_{1}, z_{1})$ , а вектор $\vec{a} = (a_{x}, a_{y}, a_{z})$ будет для нее направляющим. Значит, если мы знаем уравнение прямой, то можем вычислить координаты ее направляющего вектора, а при условии заданных координат вектора и некоторой точки, расположенной на прямой, мы можем записать ее канонические уравнения.

Разберем пару конкретных задач.

Пример 3

У нас есть прямая, заданная в трехмерном пространстве с помощью уравнения $\frac{x + 1}{4} = \frac{y}{2} = \frac{z - 3}{- 5}$ . Запишите координаты всех направляющих векторов для нее.

Решение

Чтобы получить координаты направляющего вектора, нам надо просто взять значения знаменателей из уравнения. Мы получим, что одним из направляющих векторов будет $\vec{a} = (4, 2, - 5)$ , а множество всех подобных векторов можно сформулировать как $μ \cdot \vec{a} = (4 \cdot μ, 2 \cdot μ, - 5 \cdot μ)$ . Здесь параметр $μ$ – любое действительное число (за исключением нуля).

Ответ: $(4 \cdot μ, 2 \cdot μ, - 5 \cdot μ), μ \in R, μ \neq 0$

Пример 4

Запишите канонические уравнения, если прямая в пространстве проходит через $M_{1} (0, - 3, \sqrt{2})$ и имеет направляющий вектор с координатами $(- 1, 0, 5)$ .

Решение

У нас есть данные, что $x_{1} = 0, y_{1} = - 3, z_{1} = \sqrt{2}, a_{x} = - 1, a_{y} = 0, a_{z} = 5$ . Этого вполне достаточно, чтобы сразу перейти к записи канонических уравнений.

Сделаем это:

$\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}} \Leftrightarrow \frac{x - 0}{- 1} = \frac{y - (- 3)}{0} = \frac{z - \sqrt{2}}{5} \Leftrightarrow \Leftrightarrow \frac{x}{- 1} = \frac{y + 3}{0} = \frac{z - \sqrt{2}}{5}$

Ответ: $\frac{x}{- 1} = \frac{y + 3}{0} = \frac{z - \sqrt{2}}{5}$

Эти задачи – самые простые, потому что в них есть все или почти все исходные данные для записи уравнения или координат вектора. На практике чаще можно встретить те, в которых сначала нужно находить нужные координаты, а потом записывать канонические уравнения. Примеры таких задач мы разбирали в статьях, посвященных нахождению уравнений прямой, проходящей через точку пространства параллельно заданной, а также прямой, проходящей через некоторую точку пространства перпендикулярно плоскости.

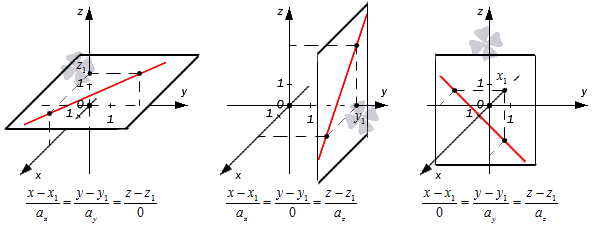
Канонические уравнения с одним или двумя a, равными нулю

Ранее мы уже говорили, что одно-два значения параметров $a_{x}, a_{y}, a_{z}$ в уравнениях могут иметь нулевые значения. При этом запись $\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}} = λ$ приобретает формальный характер, поскольку мы получаем одну или две дроби с нулевыми знаменателями. Ее можно переписать в следующем виде (при $λ \in R$ ):

$\{\begin{cases} \begin{array}{l} x = x_{1} + a_{x} \cdot λ \\ y = y_{1} + a_{y} \cdot λ \end{array} \\ z = z_{1} + a_{z} \cdot λ \end{cases}$

Рассмотрим эти случаи подробнее. Допустим, что $a_{x} = 0, a_{y} \neq 0, a_{z} \neq 0, a_{x} \neq 0, a_{y} = 0, a_{z} \neq 0$ , либо $a_{x} \neq 0, a_{y} \neq 0, a_{z} = 0$ . В таком случае нужные уравнения мы можем записать так:

В первом случае:
$\frac{x - x_{1}}{0} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}} = λ \Leftrightarrow \{\begin{cases} \begin{array}{l} x - x_{1} = 0 \\ y = y_{1} + a_{y} \cdot λ \end{array} \\ z = z_{1} + a_{z} \cdot λ \end{cases} \Leftrightarrow \{\begin{cases} x - x_{1} = 0 \\ \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}} = λ \end{cases}$
Во втором случае:
$\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{0} = \frac{z - z_{1}}{a_{z}} = λ \Leftrightarrow \{\begin{cases} \begin{array}{l} x = x_{1} + a_{x} \cdot λ \\ y - y_{1} = 0 \end{array} \\ z = z_{1} + a_{z} \cdot λ \end{cases} \Leftrightarrow \{\begin{cases} y - y_{1} = 0 \\ \frac{x - x_{1}}{a_{x}} = \frac{z - z_{1}}{a_{z}} = λ \end{cases}$
В третьем случае:
$\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{0} = λ \Leftrightarrow \{\begin{cases} \begin{array}{l} x = x_{1} + a_{x} \cdot λ \\ y = y_{1} + a_{y} \cdot λ \end{array} \\ z - z_{1} = 0 \end{cases} \Leftrightarrow \{\begin{cases} z - z_{1} = 0 \\ \frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = λ \end{cases}$

Получается, что при таком значении параметров нужные прямые находятся в плоскостях $x - x_{1} = 0, y - y_{1} = 0$ или $z - z_{1} = 0$ , которые располагаются параллельно координатным плоскостям (если $x_{1} = 0, y_{1} = 0$ либо $z_{1} = 0$ ). Примеры таких прямых показаны на иллюстрации.

Канонические уравнения с одним или двумя a, равными нулю

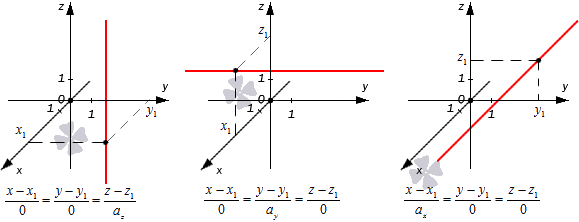
Следовательно, мы сможем записать канонические уравнения немного иначе.

В первом случае: $\frac{x - x_{1}}{0} = \frac{y - y_{1}}{0} = \frac{z - z_{1}}{a_{z}} = λ \Leftrightarrow \{\begin{cases} \begin{array}{l} x - x_{1} = 0 \\ y - y_{1} = 0 \end{array} \\ z = z_{1} + a_{z} \cdot λ, λ \in R \end{cases}$
Во втором: $\frac{x - x_{1}}{0} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{0} = λ \Leftrightarrow \{\begin{cases} \begin{array}{l} x - x_{1} = 0 \\ y = y_{1} + a_{y} \cdot λ, λ \in R \end{array} \\ z - z_{1} = 0 \end{cases}$
В третьем: $\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{0} = \frac{z - z_{1}}{0} = λ \Leftrightarrow \{\begin{cases} \begin{array}{l} x = x_{1} + a_{x} \cdot λ, λ \in R \\ y = y_{1} = 0 \end{array} \\ z - z_{1} = 0 \end{cases}$

Во всех трех случаях исходные прямые будут совпадать с координатными осями или окажутся параллельными им: $\{\begin{cases} x_{1} = 0 \\ y_{1} = 0 \end{cases}, \{\begin{cases} x_{1} = 0 \\ z_{1} = 0 \end{cases}, \{\begin{cases} y_{1} = 0 \\ z_{1} = 0 \end{cases}$ . Их направляющие векторы имеют координаты $(0, 0, a_{z}), (0, a_{y}, 0), (a_{x}, 0, 0)$ . Если обозначить направляющие векторы координатных прямых как $\vec{i}, \vec{j}, \vec{k}$ , то направляющие векторы заданных прямых будут коллинеарными по отношению к ним. На рисунке показаны эти случаи:

Канонические уравнения с одним или двумя a, равными нулю

Покажем на примерах, как применяются эти правила.

Пример 5

Найдите канонические уравнения, с помощью которых можно определить в пространстве координатные прямые $O z, O x, O y$ .

Решение

Координатные векторы $\vec{i} = (1, 0, 0), \vec{j} = (0, 1, 0), \vec{k} = (0, 0, 1)$ будут для исходных прямых направляющими. Также мы знаем, что наши прямые будут обязательно проходить через точку $O (0, 0, 0)$ , поскольку она является началом координат. Теперь у нас есть все данные, чтобы записать нужные канонические уравнения.

Для прямой $O x$ : $\frac{x}{1} = \frac{y}{0} = \frac{z}{0}$

Для прямой $O y$ : $\frac{x}{0} = \frac{y}{1} = \frac{z}{0}$

Для прямой $O z$ : $\frac{x}{0} = \frac{y}{0} = \frac{z}{1}$

Ответ: $\frac{x}{1} = \frac{y}{0} = \frac{z}{0}, \frac{x}{0} = \frac{y}{1} = \frac{z}{0}, \frac{x}{0} = \frac{y}{0} = \frac{z}{1}$ .

Пример 6

В пространстве задана прямая, которая проходит через точку $M_{1} (3, - 1, 12)$ . Также известно, что она расположена параллельно оси ординат. Запишите канонические уравнения этой прямой.

Решение

Учитывая условие параллельности, мы можем сказать, что вектор $\vec{j} = (0, 1, 0)$ будет для нужной прямой направляющим. Следовательно, искомые уравнения будут иметь вид:

$\frac{x - 3}{0} = \frac{y - (- 1)}{1} = \frac{z - 12}{0} \Leftrightarrow \frac{x - 3}{0} = \frac{y + 1}{1} = \frac{z - 12}{0}$

Ответ: $\frac{x - 3}{0} = \frac{y + 1}{1} = \frac{z - 12}{0}$

Как записать каноническое уравнение прямой, которая проходит через две заданные точки

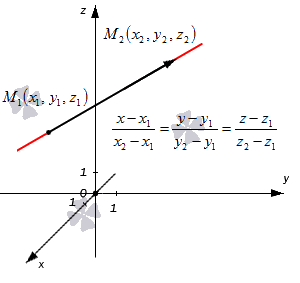
Допустим, что у нас есть две несовпадающие точки $M_{1} (x_{1}, y_{1}, z_{1})$ и $M_{2} (x_{2}, y_{2}, z_{2})$ , через которые проходит прямая. Как в таком случае мы можем сформулировать для нее каноническое уравнение?

Для начала примем вектор $\vec{M_{1} M_{2}}$ (или $\vec{M_{2} M_{1}}$ ) за направляющий вектор данной прямой. Поскольку у нас есть координаты нужных точек, сразу вычисляем координаты вектора:

$\vec{M_{1} M_{2}} = (x_{2} - x_{1}, y_{2} - y_{1}, z_{2} - z_{1})$

Далее переходим непосредственно к записи канонического уравнения, ведь все нужные данные у нас уже есть. Исходная прямая будет определяться записями следующего вида:

$\frac{x - x_{1}}{x_{2} - x_{1}} = \frac{y - y_{1}}{y_{2} - y_{1}} = \frac{z - z_{1}}{z_{2} - z_{1}} \frac{x - x_{2}}{x_{2} - x_{1}} = \frac{y - y_{2}}{y_{2} - y_{1}} = \frac{z - z_{2}}{z_{2} - z_{1}}$

Получившиеся равенства – это и есть канонические уравнения прямой, проходящей через две заданные точки. Взгляните на иллюстрацию:

Как записать каноническое уравнение прямой, которая проходит через две заданные точки

Приведем пример решения задачи.

Пример 7

в пространстве есть две точки с координатами $M_{1} (- 2, 4, 1)$ и $M_{2} (- 3, 2, - 5)$ , через которые проходит прямая. Запишите канонические уравнения для нее.

Решение

Согласно условиям, $x_{1} = - 2, y_{1} = - 4, z_{1} = 1, x_{2} = - 3, y_{2} = 2, z_{2} = - 5$ . Нам требуется подставить эти значения в каноническое уравнение:

$\frac{x - (- 2)}{- 3 - (- 2)} = \frac{y - (- 4)}{2 - (- 4)} = \frac{z - 1}{- 5 - 1} \Leftrightarrow \frac{x + 2}{- 1} = \frac{y + 4}{6} = \frac{z - 1}{- 6}$

Если мы возьмем уравнения вида $\frac{x - x_{2}}{x_{2} - x_{1}} = \frac{y - y_{2}}{y_{2} - y_{1}} = \frac{z - z_{2}}{z_{2} - z_{1}}$ , то у нас получится: $\frac{x - (- 3)}{- 3 - (- 2)} = \frac{y - 2}{2 - (- 4)} = \frac{z - (- 5)}{- 5 - 1} \Leftrightarrow \frac{x + 3}{- 1} = \frac{y - 2}{6} = \frac{z + 5}{- 6}$

Ответ: $\frac{x + 3}{- 1} = \frac{y - 2}{6} = \frac{z + 5}{- 6}$ либо $\frac{x + 3}{- 1} = \frac{y - 2}{6} = \frac{z + 5}{- 6}$ .

Преобразование канонических уравнений прямой в пространстве в другие виды уравнений

Иногда пользоваться каноническими уравнениями вида $\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}}$ не очень удобно. Для решения некоторых задач лучше использовать запись $\{\begin{cases} \begin{array}{l} x = x_{1} + a_{x} \cdot λ \\ y = y_{1} + a_{y} \cdot λ \end{array} \\ z = z_{1} + a_{z} \cdot λ \end{cases}$ . В некоторых случаях более предпочтительно определить нужную прямую с помощью уравнений двух пересекающихся плоскостей $\{\begin{cases} A_{1} x + B_{1} y + C_{1} z + D_{1} = 0 \\ A_{2} x + B_{2} y + C_{2} z + D_{2} = 0 \end{cases}$ . Поэтому в данном пункте мы разберем, как можно перейти от канонических уравнений к другим видам, если это требуется нам по условиям задачи.

Понять правила перехода к параметрическим уравнениям несложно. Сначала приравняем каждую часть уравнения к параметру $λ$ и разрешим эти уравнения относительно других переменных. В итоге получим:

$\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}} \Leftrightarrow \frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}} \Leftrightarrow \Leftrightarrow \{\begin{cases} \begin{array}{l} \frac{x - x_{1}}{a_{x}} = λ \\ \frac{y - y_{1}}{a_{y}} = λ \end{array} \\ \frac{z - z_{1}}{a_{z}} = λ \end{cases} \Leftrightarrow \{\begin{cases} \begin{array}{l} x = x_{1} + a_{x} \cdot λ \\ y = y_{1} + a_{y} \cdot λ \end{array} \\ z = z_{1} + a_{z} \cdot λ \end{cases}$

Значение параметра $λ$ может быть любым действительным числом, ведь и $x, y, z$ могут принимать любые действительные значения.

Пример 8

В прямоугольной системе координат в трехмерном пространстве задана прямая, которая определена уравнением $\frac{x - 2}{3} = \frac{y}{- 2} = \frac{z + 7}{0}$ . Запишите каноническое уравнение в параметрическом виде.

Решение

Сначала приравниваем каждую часть дроби к $λ$ .

$\frac{x - 2}{3} = \frac{y}{- 2} = \frac{z + 7}{0} \Leftrightarrow \{\begin{cases} \begin{array}{l} \frac{x - 2}{3} = λ \\ \frac{y}{- 2} = λ \end{array} \\ \frac{z + 7}{0} = λ \end{cases}$

Теперь разрешаем первую часть относительно $x$ , вторую – относительно $y$ , третью – относительно $z$ . У нас получится:

$\{\begin{cases} \begin{array}{l} \frac{x - 2}{3} = λ \\ \frac{y}{- 2} = λ \end{array} \\ \frac{z + 7}{0} = λ \end{cases} \Leftrightarrow \{\begin{cases} \begin{array}{l} x = 2 + 3 \cdot λ \\ y = - 2 \cdot λ \end{array} \\ z = - 7 + 0 \cdot λ \end{cases} \Leftrightarrow \{\begin{cases} \begin{array}{l} x = 2 + 3 \cdot λ \\ y = - 2 \cdot λ \end{array} \\ z = - 7 \end{cases}$

Ответ: $\{\begin{cases} \begin{array}{l} x = 2 + 3 \cdot λ \\ y = - 2 \cdot λ \end{array} \\ z = - 7 \end{cases}$

Следующим нашим шагом будет преобразование канонических уравнений в уравнение двух пересекающихся плоскостей (для одной и той же прямой).

Равенство $\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}}$ нужно для начала представить в виде системы уравнений:

$\{\begin{cases} \begin{array}{l} \frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} \\ \frac{x - x_{1}}{a_{x}} = \frac{z - z_{1}}{a_{x}} \end{array} \\ \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}} \end{cases}$

Поскольку $\frac{p}{q} = \frac{r}{s}$ мы понимаем как $p \cdot s = q \cdot r$ , то можно записать:

$\{\begin{cases} \begin{array}{l} \frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} \\ \frac{x - x_{1}}{a_{x}} = \frac{z - z_{1}}{a_{z}} \end{array} \\ \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}} \end{cases} \Leftrightarrow \{\begin{cases} \begin{array}{l} a_{y} \cdot (x - x_{1}) = a_{x} \cdot (y - y_{1}) \\ a_{z} \cdot (x - x_{1}) = a_{x} \cdot (z - z_{1}) \end{array} \\ a_{z} \cdot (y - y_{1}) = a_{y} \cdot (z - z_{1}) \end{cases} \Leftrightarrow \Leftrightarrow \{\begin{cases} \begin{array}{l} a_{y} \cdot x - a_{x} \cdot y + a_{x} \cdot y_{1} - a_{y} \cdot x_{1} = 0 \\ a_{z} \cdot x - a_{x} \cdot z + a_{x} \cdot z_{1} - a_{z} \cdot x_{1} = 0 \end{array} \\ a_{z} \cdot y - a_{y} \cdot z + a_{y} \cdot z_{1} - a_{z} \cdot y_{1} = 0 \end{cases}$

В итоге у нас вышло, что:

$\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}} \Leftrightarrow \{\begin{cases} \begin{array}{l} a_{y} \cdot x - a_{x} \cdot y + a_{x} \cdot y_{1} - a_{y} \cdot x_{1} = 0 \\ a_{z} \cdot x - a_{x} \cdot z + a_{x} \cdot z_{1} - a_{z} \cdot x_{1} = 0 \end{array} \\ a_{z} \cdot y - a_{y} \cdot z + a_{y} \cdot z_{1} - a_{z} \cdot y_{1} = 0 \end{cases}$

Выше мы отмечали, что все три параметра $a$ не могут одновременно быть нулевыми. Значит, ранг основной матрицы системы будет равен $2$ , поскольку $|\begin{matrix} a_{y} & - a_{x} & 0 \\ a_{z} & 0 & - a_{x} \\ 0 & a_{z} & - a_{y} \end{matrix}| = 0$ и один из определителей второго порядка не равен $0$ :

$|\begin{matrix} a_{y} & - a_{x} \\ a_{z} & 0 \end{matrix}| = a_{x} \cdot a_{z}, |\begin{matrix} a_{y} & 0 \\ a_{z} & - a_{x} \end{matrix}| = a_{x} \cdot a_{y}, |\begin{matrix} - a_{x} & 0 \\ 0 & - a_{x} \end{matrix}| = a_{x}^{2} |\begin{matrix} a_{y} & - a_{x} \\ 0 & a_{z} \end{matrix}| = a_{y} \cdot a_{z}, |\begin{matrix} a_{y} & 0 \\ 0 & - a_{y} \end{matrix}| = - a_{y}^{2}, |\begin{matrix} - a_{x} & 0 \\ a_{z} & - a_{y} \end{matrix}| = a_{x} \cdot a_{y} |\begin{matrix} a_{z} & 0 \\ 0 & a_{z} \end{matrix}| = a_{z}^{2}, |\begin{matrix} a_{z} & - a_{x} \\ 0 & - a_{y} \end{matrix}| = - a_{y} \cdot a_{z}, |\begin{matrix} 0 & - a_{x} \\ a_{z} & - a_{y} \end{matrix}| = a_{x} \cdot a_{z}$

Это дает нам возможность исключить одно уравнение из наших расчетов. Таким образом, канонические уравнения прямой можно преобразовать в систему из двух линейных уравнений, которые будут содержать $3$ неизвестных. Они и будут нужными нам уравнениями двух пересекающихся плоскостей.

Рассуждение выглядит довольно сложным, однако на практике все делается довольно быстро. Продемонстрируем это на примере.

Пример 9

Прямая задана каноническим уравнением $\frac{x - 1}{2} = \frac{y}{0} = \frac{z + 2}{0}$ . Напишите для нее уравнение пересекающихся плоскостей.

Решение

Начнем с попарного приравнивания дробей.

$\frac{x - 1}{2} = \frac{y}{0} = \frac{z + 2}{0} \Leftrightarrow \{\begin{cases} \begin{array}{l} \frac{x - 1}{2} = \frac{y}{0} \\ \frac{x - 1}{2} = \frac{z + 2}{0} \end{array} \\ \frac{y}{0} = \frac{z + 2}{0} \end{cases} \Leftrightarrow \Leftrightarrow \{\begin{cases} \begin{array}{l} 0 \cdot (x - 1) = 2 y \\ 0 \cdot (x - 1) = 2 \cdot (z + 2) \end{array} \\ 0 \cdot y = 0 \cdot (z + 2) \end{cases} \Leftrightarrow \{\begin{cases} \begin{array}{l} y = 0 \\ z + 2 = 0 \end{array} \\ 0 = 0 \end{cases}$

Теперь исключаем из расчетов последнее уравнение, потому что оно будет верным при любых $x, y$ и $z$ . В таком случае $\frac{x - 1}{2} = \frac{y}{0} = \frac{z + 2}{0} \Leftrightarrow \{\begin{cases} y = 0 \\ z + 2 = 0 \end{cases}$ .

Это и есть уравнения двух пересекающихся плоскостей, которые при пересечении образуют прямую, заданную с помощью уравнения $\frac{x - 1}{2} = \frac{y}{0} = \frac{z + 2}{0}$

Ответ: $\{\begin{cases} y = 0 \\ z + 2 = 0 \end{cases}$

Пример 10

Прямая задана уравнениями $\frac{x + 1}{2} = \frac{y - 2}{1} = \frac{z - 5}{- 3}$ , найдите уравнение двух плоскостей, пересекающихся по данной прямой.

Решение

Приравниваем дроби попарно.

$\frac{x + 1}{2} = \frac{y - 2}{1} = \frac{z - 5}{- 3} \Leftrightarrow \{\begin{cases} \begin{array}{l} \frac{x + 1}{2} = \frac{y - 2}{1} \\ \frac{x + 1}{2} = \frac{z - 5}{- 3} \end{array} \\ \frac{y - 2}{1} = \frac{z - 5}{- 3} \end{cases} \Leftrightarrow \Leftrightarrow \{\begin{cases} \begin{array}{l} 1 \cdot (x + 1) = 2 \cdot (y - 2) \\ - 3 \cdot (x + 1) = 2 \cdot (z - 5) \end{array} \\ - 3 \cdot (y - 2) = 1 \cdot (z - 5) \end{cases} \Leftrightarrow \{\begin{cases} \begin{array}{l} x - 2 y + 5 = 0 \\ 3 x + 2 z - 7 = 0 \end{array} \\ 3 y + 7 - 11 = 0 \end{cases}$

Получаем, что определитель основной матрицы полученной системы будет равен $0$ :

$|\begin{matrix} 1 & - 2 & 0 \\ 3 & 0 & 2 \\ 0 & 3 & 1 \end{matrix}| = 1 \cdot 0 \cdot 1 + (- 2) \cdot 2 \cdot 0 + 0 \cdot 3 \cdot 3 - 0 \cdot 0 \cdot 0 - 1 \cdot 2 \cdot 3 - (- 2) \cdot 3 \cdot 1 = 0$

Минор второго порядка нулевым при этом не будет: $|\begin{matrix} 1 & - 2 \\ 3 & 0 \end{matrix}| = 1 \cdot 0 - (- 2) \cdot 3 = 6$ . Тогда мы можем принять его в качестве базисного минора.

В итоге мы можем вычислить ранг основной матрицы системы $\{\begin{cases} x - 2 y + 5 = 0 \\ \begin{array}{l} 3 x + 2 z - 7 = 0 \\ 3 y + z - 11 = 0 \end{array} \end{cases}$ . Это будет 2. Третье уравнение исключаем из расчета и получаем:

$\{\begin{cases} x - 2 y + 5 = 0 \\ \begin{array}{l} 3 x + 2 z - 7 = 0 \\ 3 y + z - 11 = 0 \end{array} \end{cases} \Leftrightarrow \{\begin{cases} x - 2 y + 5 = 0 \\ 3 x + 2 z - 7 = 0 \end{cases}$

Ответ: $\{\begin{cases} x - 2 y + 5 = 0 \\ 3 x + 2 z - 7 = 0 \end{cases}$

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.