Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач

8 августа 2023
7 минут
9 353

Содержание:

Нормальное уравнение прямой – описание и пример
Приведение общего уравнения прямой к нормальному виду
Нахождение расстояния от точки до прямой на плоскости

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

В данной статье рассмотрим нормальное уравнение прямой на заданной плоскости. Получим нормальное уравнение, покажем не примере, дадим определение нормирующего множителя и разберем приведение общего уравнения к нормальному виду. Заключительной части посвятим основному приложению нормального уравнения прямой, то есть нахождение расстояние от точки до прямой на плоскости.

Нормальное уравнение прямой – описание и пример

Рассмотрим выведение нормального уравнения.

Фиксируем на плоскости систему координат $О х у$ $О х у$ , где задаем прямую с точкой, через которую она проходит с нормальным вектором прямой. Нормальному вектору прямой дадим обозначение $\to n$ $\vec{n}$ . Его начало обозначено точкой $O$ $O$ . координатами являются $cos α$ $\cos α$ и $cos β$ $\cos β$ , углы которых расположены между вектором $\to n$ $\vec{n}$ и положительными осями $О x$ $О x$ и $O y$ $O y$ . Это запишется так: $\to n = (cos α, cos β)$ $\vec{n} = (\cos α, \cos β)$ . Прямая проходит через точку $A$ $A$ с расстоянием равным $p$ $p$ , где $p \geq 0$ $p \geq 0$ от начальной точки $O$ $O$ при положительном направлении вектора $\to n$ $\vec{n}$ . Если $р = 0$ $р = 0$ , тогда $A$ $A$ считается совпадающей с точкой координат. Отсюда имеем, что $open O A | = p$ $openO A| = p$ . Получаем уравнение, при помощи которого задается прямая.

Имеем, что точка с координатами $M (x, y)$ $M (x, y)$ расположена на прямой тогда и только тогда, когда числовая проекция вектора $- - \to O M$ $\vec{O M}$ по направлению вектора $\to n$ $\vec{n}$ равняется $p$ $p$ , значит при выполнении условия $n p_{\to n} - - \to O M = p$ $n p_{\vec{n}} \vec{O M} = p$ .

Нормальное уравнение прямой – описание и пример

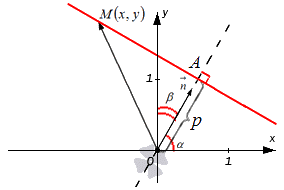
$- - \to O M$ $\vec{O M}$ является радиус-вектором точки с координатами $M (x, y)$ $M (x, y)$ , значит $- - \to O M = (x, y)$ $\vec{O M} = (x, y)$ .

Применив определение скалярного произведения векторов, получим равенство вида: $(\to n, - - \to O M) = open \to n ∣ ∣ \cdot n p_{\to n} - - \to O M = 1 \cdot n p_{\to n} - - \to O M = n p_{\to n} - - \to O M = p$ $(\vec{n}, \vec{O M}) = open\vec{n}| \cdot n p_{\vec{n}} \vec{O M} = 1 \cdot n p_{\vec{n}} \vec{O M} = n p_{\vec{n}} \vec{O M} = p$

Тогда это же произведение будет иметь вид в координатной форме: $(\to n, - - \to O M) = cos α \cdot x + cos β \cdot y$ $(\vec{n}, \vec{O M}) = \cos α \cdot x + \cos β \cdot y$

Отсюда $cos α \cdot x + cos β \cdot y = p$ $\cos α \cdot x + \cos β \cdot y = p$ или $cos α \cdot x + cos β \cdot y - p = 0$ $\cos α \cdot x + \cos β \cdot y - p = 0$ . Было выведено нормальное уравнение прямой.

Определение 1

Уравнение вида $cos α \cdot x + cos β \cdot y - p = 0$ $\cos α \cdot x + \cos β \cdot y - p = 0$ называется нормальным уравнением прямой или нормированным уравнением прямой. Иначе говоря, уравнение прямой в нормальном виде.

Понятно, что такое уравнение представляет собой общее уравнение прямой $A x + B y + C = 0$ $A x + B y + C = 0$ , где $A$ $A$ и $B$ $B$ имеют значения, при которых длина вектора $\to n = (A, B)$ $\vec{n} = (A, B)$ равна $1$ $1$ , а $C$ $C$ является неотрицательным числом.

Теперь рассмотрим его геометрический смысл. Нормальное уравнение прямой вида $cos α \cdot x + cos β \cdot y - p = 0$ $\cos α \cdot x + \cos β \cdot y - p = 0$ задает в системе координат $О х у$ $О х у$ на плоскости прямую с наличием нормального вектора единичной длины $\to n = (cos α, cos β)$ $\vec{n} = (\cos α, \cos β)$ , которая располагается на расстоянии равном $p$ $p$ от начала координат по положительному направлению вектора $\to n$ $\vec{n}$ .

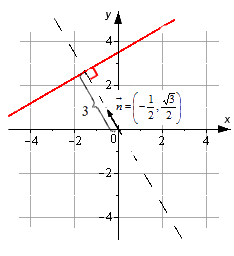
Если дано уравнение прямой вида $- \frac{1}{2} \cdot x + \frac{\sqrt{3}}{2} \cdot y - 3 = 0$ $- \frac{1}{2} \cdot x + \frac{\sqrt{3}}{2} \cdot y - 3 = 0$ , то на плоскости задается прямая, у которой нормальный вектор с координатами $(- \frac{1}{2}, \frac{\sqrt{3}}{2})$ $(- \frac{1}{2}, \frac{\sqrt{3}}{2})$ . Удаление прямой от начала координат идет по направлению, совпадающему с направлением нормального вектора $\to n = (- \frac{1}{2}, \frac{\sqrt{3}}{2})$ $\vec{n} = (- \frac{1}{2}, \frac{\sqrt{3}}{2})$ .

Нормальное уравнение прямой – описание и пример

Приведение общего уравнения прямой к нормальному виду

Часто решение задач подразумевает использование нормального уравнения прямой, но само оно не дается в нормальном виде, поэтому необходимо для начала приводить к нормальному виду, после чего выполнять необходимые вычисления.

Нормальное уравнение получают из общего уравнения прямой. Когда на плоскости задается другим уравнением, то необходимо привести его к общему виду, после чего возможно приведение к нормальному. Если рассмотреть на примере, то это будет выглядеть так.

Для приведения общего уравнения прямой $A x + B x + C = 0$ $A x + B x + C = 0$ к нормальному необходимо обе части умножить на нормирующий множитель,который имеет значение $\pm \frac{1}{\sqrt{A^{2} + B^{2}}}$ $\pm \frac{1}{\sqrt{A^{2} + B^{2}}}$ . Его знак определяется при помощи противоположности знака слагаемого $C$ $C$ . При $С = 0$ $С = 0$ знак выбирается произвольно.

Пример 1

Привести уравнение прямой $3 x - 4 y - 16 = 0$ $3 x - 4 y - 16 = 0$ к нормальному виду.

Решение

Из общего уравнения видно, что $А = 3, В = - 4, С = - 16$ $А = 3, В = - 4, С = - 16$ . Так как значение $C$ $C$ отрицательное, необходимо брать положительный знак для формулы. Перейдем к вычислению нормирующего множителя:

$\frac{1}{\sqrt{A^{2} + B^{2}}} = \frac{1}{\sqrt{3^{2} + (- 4)^{2}}} = \frac{1}{5}$ $\frac{1}{\sqrt{A^{2} + B^{2}}} = \frac{1}{\sqrt{3^{2} + (- 4)^{2}}} = \frac{1}{5}$

Теперь необходимо умножить обе части уравнения на одну пятую. Получим, что $\frac{1}{5} \cdot (3 x - 4 y - 16) = 0 \Leftrightarrow \frac{3}{5} \cdot x - \frac{4}{5} \cdot y - \frac{16}{5} = 0$ $\frac{1}{5} \cdot (3 x - 4 y - 16) = 0 \Leftrightarrow \frac{3}{5} \cdot x - \frac{4}{5} \cdot y - \frac{16}{5} = 0$ .

Нормальное уравнение по заданной прямой найдено.

Ответ: $\frac{3}{5} \cdot x - \frac{4}{5} \cdot y - \frac{16}{5} = 0$ $\frac{3}{5} \cdot x - \frac{4}{5} \cdot y - \frac{16}{5} = 0$ .

Пример 2

Получить нормальное уравнение прямой $y = \frac{1}{3} x$ $y = \frac{1}{3} x$ .

Решение

По условию имеем, что общее уравнение прямой $\frac{1}{3} x - y = 0$ $\frac{1}{3} x - y = 0$ . Очевидно, что $С = 0$ $С = 0$ , значит знак нормирующего множителя не имеет значения. Выбираем со знаком « $+$ $+$ ». Тогда выражение примет вид:

$\frac{1}{\sqrt{A^{2} + B^{2}}} = \frac{1}{\sqrt{{(\frac{1}{3})}^{2} + (- 1)^{2}}} = \frac{3}{\sqrt{10}}$ $\frac{1}{\sqrt{A^{2} + B^{2}}} = \frac{1}{\sqrt{{(\frac{1}{3})}^{2} + (- 1)^{2}}} = \frac{3}{\sqrt{10}}$

Обе части умножаем на нормированный множитель, получаем, что нормальное уравнение прямой имеет вид $\frac{1}{\sqrt{10}} x - \frac{3}{\sqrt{10}} y = 0$ $\frac{1}{\sqrt{10}} x - \frac{3}{\sqrt{10}} y = 0$ .

Ответ: $\frac{1}{\sqrt{10}} x - \frac{3}{\sqrt{10}} y = 0$ $\frac{1}{\sqrt{10}} x - \frac{3}{\sqrt{10}} y = 0$ .

Нахождение расстояния от точки до прямой на плоскости

В данном пункте рассмотрим важное приложение нормального уравнения прямой – нахождение расстояния от заданной точки до заданной прямой на плоскости.

Расстояние от точки $M_{0} (x_{0}, y_{0})$ $M_{0} (x_{0}, y_{0})$ до прямой с нормальным уравнением $cos α \cdot x + cos β \cdot y - p = 0$ $\cos α \cdot x + \cos β \cdot y - p = 0$ задается буквой $p$ $p$ . Вычисление расстояния р производится по формуле $p = open cos α \cdot x_{0} + cos β \cdot y_{0} - p |$ $p = open\cos α \cdot x_{0} + \cos β \cdot y_{0} - p|$ . Для того, чтобы найти расстояние от точки до прямой, нужно сделать подстановку координат этой точки в левую часть уравнения и работать с абсолютной величиной полученного значения. С подробным выводом формулы можно ознакомиться в статье нахождения расстояния от точки до прямой. Имеется альтернативный способ его вычисления.

Пример 3

Найти расстояния от точки с координатами $M_{0} (- 2, 1)$ $M_{0} (- 2, 1)$ к прямой с нормальным уравнением $\frac{2}{3} x - \frac{\sqrt{5}}{2} y - 1 = 0$ $\frac{2}{3} x - \frac{\sqrt{5}}{2} y - 1 = 0$ .

Решение

По условию имеем, что $x_{0} = - 2, y_{0} = 1, cos α = \frac{2}{3}, cos β = - \frac{\sqrt{5}}{3}, p = 1$ $x_{0} = - 2, y_{0} = 1, \cos α = \frac{2}{3}, \cos β = - \frac{\sqrt{5}}{3}, p = 1$ .

Применим формулу для вычисления расстояния от точки до прямой. Получим, что:

$p = open cos α \cdot x_{0} + cos β \cdot y_{0} - p | = open \frac{2}{3} \cdot (- 2) - \frac{\sqrt{5}}{3} \cdot 1 - 1 ∣ ∣ = open - \frac{7 + \sqrt{5}}{3} ∣ ∣ = \frac{7 + \sqrt{5}}{3}$ $p = open\cos α \cdot x_{0} + \cos β \cdot y_{0} - p| = open\frac{2}{3} \cdot (- 2) - \frac{\sqrt{5}}{3} \cdot 1 - 1| = open- \frac{7 + \sqrt{5}}{3}| = \frac{7 + \sqrt{5}}{3}$

Ответ: $\frac{7 + \sqrt{5}}{3}$ $\frac{7 + \sqrt{5}}{3}$ .

Пример 4

Вычислить расстояние от точки с координатами $M_{0} (- 2, - 3)$ $M_{0} (- 2, - 3)$ до прямой $\frac{x - 1}{- 2} = \frac{y + 3}{3}$ $\frac{x - 1}{- 2} = \frac{y + 3}{3}$ .

Решение

Начнем решение с приведения уравнения заданной прямой к нормальному виду. Для начала необходимо привести к общему виду. Получим:

$\frac{x - 1}{- 2} = \frac{y + 3}{3} \Leftrightarrow 3 \cdot (x - 1) = - 2 \cdot (y + 3) \Leftrightarrow 3 x + 2 y + 3 = 0$ $\frac{x - 1}{- 2} = \frac{y + 3}{3} \Leftrightarrow 3 \cdot (x - 1) = - 2 \cdot (y + 3) \Leftrightarrow 3 x + 2 y + 3 = 0$

Проведем вычисление нормирующего множителя по формуле: $- \frac{1}{\sqrt{A^{2} + B^{2}}} = - \frac{1}{\sqrt{3^{2} + 2^{2}}} = - \frac{1}{\sqrt{13}}$ $- \frac{1}{\sqrt{A^{2} + B^{2}}} = - \frac{1}{\sqrt{3^{2} + 2^{2}}} = - \frac{1}{\sqrt{13}}$ .

Следующим действием будет умножение обоих частей уравнения $3 x + 2 y + 3 = 0$ $3 x + 2 y + 3 = 0$ на нормирующий множитель.

Получаем: $- \frac{3}{\sqrt{13}} \cdot x - \frac{2}{\sqrt{13}} \cdot y - \frac{3}{\sqrt{13}} = 0$ $- \frac{3}{\sqrt{13}} \cdot x - \frac{2}{\sqrt{13}} \cdot y - \frac{3}{\sqrt{13}} = 0$

Было произведено получение нормального уравнения прямой. Чтобы найти расстояние, необходимо использовать абсолютную величину и подставить в формулу для нахождения искомого значения.

Тогда $p = open - \frac{3}{\sqrt{13}} \cdot (- 2) - \frac{2}{\sqrt{13}} \cdot (- 3) - \frac{3}{\sqrt{13}} ∣ ∣ = open \frac{9}{\sqrt{13}} ∣ ∣ = \frac{9}{\sqrt{13}}$ $p = open- \frac{3}{\sqrt{13}} \cdot (- 2) - \frac{2}{\sqrt{13}} \cdot (- 3) - \frac{3}{\sqrt{13}}| = open\frac{9}{\sqrt{13}}| = \frac{9}{\sqrt{13}}$ .

Ответ: $\frac{9}{\sqrt{13}}$ $\frac{9}{\sqrt{13}}$ .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter