Нормальное уравнение плоскости: описание, примеры, решение задач

Содержание:

26 апреля 2023
10 минут
2018

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Статья раскрывает суть нормального (нормированного) уравнения и показывает, при каких видах задач его чаще всего применяют. Рассмотрим выведение нормального уравнения плоскости с примерами решений. Приведем примеры приведения общего уравнения плоскости к нормальному виду. Решим задачи по нахождению расстояния от точки до плоскости при помощи нормального уравнения плоскости.

Нормальное уравнение плоскости – описание и пример

Возьмем прямоугольную систему координат $О х у z$ трехмерного пространства. Если плоскость удалена на расстояние $p \geq 0$ в положительном направлении нормального вектора $\vec{n}$ . Возьмем за единицу длину вектора $\vec{n}$ . Получим, что координатами направляющего косинуса являются $\vec{n} = (\cos α, \cos β, \cos γ)$ , тогда $|\vec{n}| = \sqrt{\cos^{2} α, \cos^{2} β, \cos^{2} γ} = 1$ .

Примем обозначение $|O N|$ за расстояние от точки до плоскости, таким образом, точка $N$ принадлежит плоскости, где длиной отрезка $O N$ будет значение $p$ . Представим это на рисунке, изображенном ниже.

Нормальное уравнение плоскости – описание и пример

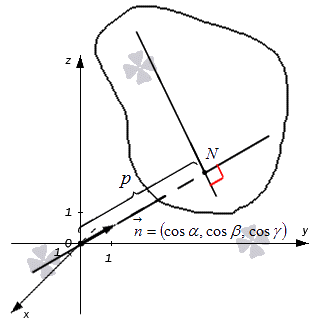
Теперь найдем уравнение заданной плоскости.

В трехмерном пространстве обозначим точку $M (x, y, z)$ . Отсюда получим, что $\vec{O M}$ , являющийся ее радиус вектором, с координатами $(x, y, z)$ . Запись примет вид $\vec{O M} = (x, y, z)$ . Отсюда получаем, что плоскость определена множеством точек $M (x, y, z)$ , тогда числовая проекция вектора $\vec{O M}$ по направлению $\vec{n}$ равна значению $p$ . Запись принимает вид $n p_{\vec{n}} \vec{O M} = p$ . Рассмотрим на приведенном ниже рисунке.

Нормальное уравнение плоскости – описание и пример

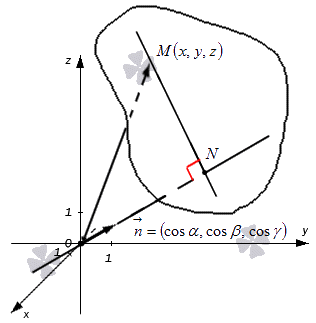
Из вышесказанного получим, что определение скалярного произведения векторов по формуле $\vec{n} = (\cos α, \cos β, \cos γ)$ и $\vec{O M} = (x, y, z)$ в результате дают равенство

$(\vec{n}, \vec{O M}) = |\vec{n}| \cdot |\vec{O M}| \cdot \cos (\hat{\overset{⇀}{n}, \vec{O M}}) = |\vec{n}| \cdot n p_{\vec{n}} \vec{O M} = 1 \cdot p = p$

Данная формула представляет скалярное произведение в координатной форме. Тогда получаем следующее выражение:

$(\vec{n}, \vec{O M}) = \cos α \cdot x + \cos β \cdot y + \cos γ \cdot z$

При сопоставлении двух последних равенств получаем уравнение плоскости такого вида $\cos α \cdot x + \cos β \cdot y + \cos γ \cdot z = p$ . Упростим выражения. Для этого необходимо перенести значение $p$ в левую сторону, получим $\cos α \cdot x + \cos β \cdot y + \cos γ \cdot z - p = 0$ .

Определение 1

$\cos α \cdot x + \cos β \cdot y + \cos γ \cdot z - p = 0$ называют нормальным уравнением плоскости или уравнением плоскости в нормальном виде. Реже его называют нормированным уравнением заданной плоскости.

Теперь заданное в прямоугольной системе координат $О х у z$ нормальное уравнение принимает вид $\cos α \cdot x + \cos β \cdot y + \cos γ \cdot z - p = 0$ . Р имеет значение расстояния положительного направления единичного нормального вектора плоскости $\vec{n} = (\cos α, \cos β, \cos γ)$ .

Чаще всего косинус не представляется явно в уравнении плоскости, потому как $\cos α, \cos β$ и $\cos γ$ является некоторыми действительными числами, сумма квадратов которых равна единице.

Рассмотрим пример нормального уравнения плоскости.

Если имеется плоскость, заданная в прямоугольной системе координат $O x y z$ при помощи уравнения нормального вида, $- \frac{1}{4} \cdot x - \frac{3}{4} \cdot y + \frac{\sqrt{6}}{4} \cdot z - 7 = 0$ .

Отсюда $\cos α = - \frac{1}{4}, \cos β = - \frac{3}{4}, \cos γ = \frac{\sqrt{6}}{4}$ .

Из выражения находим, что $(- \frac{1}{4}, - \frac{3}{4}, \frac{\sqrt{6}}{4})$ - координаты нормального вектора плоскости $\vec{n}$ . Его длина вычисляется из формулы $|\vec{n}| = \sqrt{{(- \frac{1}{4})}^{2} + {(- \frac{3}{4})}^{2} + {(\frac{\sqrt{6}}{4})}^{2}} = 1$ . Плоскость располагается относительно координат в направлении вектора $\vec{n}$ на расстоянии $7$ единиц, потому как $p = 7$ .

Отсюда ясно, что нормальное уравнение плоскости представляет собой общее уравнение плоскости $A x + B y + C z + D = 0$ , где $A, B, C$ – некоторые действительные числа, при которых длина нормального вектора плоскости $\vec{n} = (A, B, C)$ равняется $1$ , причем $D$ является неотрицательным числом.

Чтобы выявить, является представленное уравнение нормальным уравнением плоскости, необходимо выполнение обоих условий $\vec{n} = \sqrt{\cos^{2} α + \cos^{2} β + \cos^{2} γ} = 1$ и $p \geq 0$ , тогда получим уравнение плоскости нормального вида. При невыполнении хотя бы одного условия, уравнение не является нормальным.

Рассмотрим на примере.

Пример 1

Выявить уравнение плоскости нормального вида из заданных уравнений:

$\frac{1}{7} x - \frac{4}{7} y + \frac{4 \sqrt{2}}{7} - \sqrt{3} = 0 \frac{1}{3} x + \frac{\sqrt{7}}{6} y - \frac{5}{6} z + \frac{2}{5} = 0 \frac{1}{3} x + \frac{1}{2} y + \frac{1}{4} z - 11 = 0$

Решение

Начнем решение с первого уравнения. Для этого необходимо проверить, равняется ли длина нормального вектора $\vec{n} = (\frac{1}{7}, - \frac{4}{7}, \frac{4 \sqrt{2}}{7})$ единице.

Вычисляем длину по формуле и получаем: $|\vec{n}| = \sqrt{{(\frac{1}{7})}^{2} + {(- \frac{4}{7})}^{2} + {(\frac{4 \sqrt{2}}{7})}^{2}} = \sqrt{\frac{1}{49} + \frac{16}{49} + \frac{32}{49}} = 1$

Необходимо поработать с числом $p$ , так как его значение должно быть положительным. Это верно, так как $p = \sqrt{3}$ . Значит, первое заданное уравнение плоскости можно считать уравнением плоскости в нормальном виде.

Второе уравнение из заданных нельзя считать нормальным уравнением плоскости, так как условие $p \geq 0$ не выполняется, ибо в данном уравнении $p = - \frac{2}{5}$ .

Третье уравнение имеет нормальный вектор с координатами $\vec{n} = (\frac{1}{3}, \frac{1}{2}, \frac{1}{4})$ , длина которого не равняется единице из вычислений:

$|\vec{n}| = \sqrt{{(\frac{1}{3})}^{2} + {(\frac{1}{2})}^{2} + {(\frac{1}{4})}^{2}} = \sqrt{\frac{1}{9} + \frac{1}{4} + \frac{1}{16}} = \frac{\sqrt{61}}{12} \neq 1$

Отсюда следует, что его нельзя считать за уравнение плоскости в нормальном виде.

Ответ: $\frac{1}{7} x - \frac{4}{7} y + \frac{4 \sqrt{2}}{7} z - \sqrt{3} = 0$ уравнение является нормальным уравнением плоскости.

Приведение общего уравнения плоскости к нормальному виду

Для приведения уравнения плоскости $A x + B y + C z + D = 0$ к нормальному виду, обе части умножаются на нормированный множитель $\pm \frac{1}{\sqrt{A^{2} + B^{2} + C^{2}}}$ . Знак определятся по числу $D$ , он должен быть противоположным значения числа $D$ .

Когда $D = 0$ , знак может быть любым.

Определение 2

Нормальным уравнением плоскости считается общее уравнение плоскости после умножения на нормирующий множитель, потому как длина вектора с кооординатами $(\pm \frac{A}{\sqrt{A^{2} + B^{2} + C^{2}}}, \pm \frac{B}{\sqrt{A^{2} + B^{2} + C^{2}}}, \pm \frac{C}{\sqrt{A^{2} + B^{2} + C^{2}}})$ равна $1$ .

Отсюда получаем, что $\sqrt{(\pm \frac{A}{\sqrt{A^{2} + B^{2} + C^{2}}}, \pm \frac{B}{\sqrt{A^{2} + B^{2} + C^{2}}}, \pm \frac{C}{\sqrt{A^{2} + B^{2} + C^{2}}})} = \sqrt{\frac{A^{2} + B^{2} + C^{2}}{A^{2} + B^{2} + C^{2}}} = 1$ .

Знак множителя необходим для того, что проверять выполнимость условия $p \geq 0$ .

Пример 2

Привести уравнение $2 x - 3 y + z + 5 = 0$ к нормальному виду.

Решение

Из условия имеем, что $A = 2, B = - 3, C = 1, D = 5$ . Исходя из того, что $D$ является положительным числом, нормирующий множитель дожжен иметь противоположный знак. Отсюда получим, что получим отрицательный результат.

$- \frac{1}{\sqrt{A^{2} + B^{2} + C^{2}}} = - \frac{1}{\sqrt{2^{2} + (- 3)^{2} + 1^{2}}} = - \frac{1}{\sqrt{14}}$

Чтобы получить искомое нормальное уравнение плоскости, обе части уравнения необходимо умножить на нормирующий множитель. Получим:

$- \frac{1}{\sqrt{14}} \cdot (2 x - 3 y + z + 5) = - \frac{1}{\sqrt{14}} \cdot 0 \Leftrightarrow \Leftrightarrow - \frac{2}{\sqrt{14}} x + \frac{3}{\sqrt{14}} y - \frac{1}{\sqrt{14}} z - \frac{5}{\sqrt{14}} = 0$

Ответ: $- \frac{2}{\sqrt{14}} x + \frac{3}{\sqrt{14}} y - \frac{1}{\sqrt{14}} z - \frac{5}{\sqrt{14}} = 0$ .

Пример 3

Написать нормальное уравнение плоскости, если оно задано уравнением $3 x - 4 z = 0$ прямоугольной системы координат $O x y z$ .

Решение

Из условия видно, что $A = 3, B = 0, C = - 4, D = 0$ . Знака перед множителем нет, потому как $D = 0$ . Значит, возьмем со знаком « $+$ ». Получаем выражение вида:

$\frac{1}{\sqrt{A^{2} + B^{2} + C^{2}}} = \frac{1}{\sqrt{3^{2} + 0^{2} + (- 4)^{2}}} = \frac{1}{5}$

При умножении обеих частей уравнения на нормирующий множитель, получаем уравнение плоскости нормального вида $\frac{3}{5} x - \frac{4}{5} z = 0$ .

Ответ: $\frac{3}{5} x - \frac{4}{5} z = 0$ .

Нахождение расстояния от точки до плоскости

Теперь раскроем тему нормального уравнения плоскости, где уравнение плоскости нормального вида применимо для нахождения расстояния от заданной точки в пространстве до плоскости.

При заданной системе координат $О х у z$ трехмерного пространства имеем плоскость с уравнением $\cos α \cdot x + \cos β \cdot y + \cos γ \cdot z - p = 0$ , где необходимо определить расстояние от $p$ до точки $M_{0} (x_{0}, y_{0}, z_{0})$ заданной плоскости. Его вычисляют по формуле $p = |\cos α \cdot x_{0} + \cos β \cdot y_{0} + \cos γ \cdot z_{0} - p|$ . Само расстояние является числом, которое получается при подстановке координат точки в левую сторону уравнения. Для вывода формулы необходимо обратиться к статье расстояния от точки до плоскости.

Пример 4

Имеется уравнение плоскости вида $- \frac{1}{3} x + \frac{2}{3} y - \frac{2}{3} z - 1 = 0$ , которое располагается в прямоугольной системе координат. Определить расстояние от точки с координатами $M_{0} (1, - 3, 0)$ до плоскости.

Решение

Координаты точки $M$ необходимо подставить в левую часть уравнения плоскости. Тогда получаем:

$- \frac{1}{3} \cdot 1 + \frac{2}{3} \cdot (- 3) - \frac{2}{3} \cdot 0 - 1 = 0$

Искомое расстояние – величина абсолютная, значит $p = |- 3 \frac{1}{3}| = 3 \frac{1}{3}$ .

Ответ: $3 \frac{1}{3}$ .

Если плоскость задана другим уравнением, а необходимо произвести вычисление от заданной точки до плоскости, необходимо привести уравнение к виду нормального уравнения плоскости, используя формулу $p = |\cos α \cdot x_{0} + \cos β \cdot y_{0} + \cos γ \cdot z_{0} - p|$ .

Пример 5

Найти расстояние от заданной точки с координатами $M_{0} (5, - 1, 2)$ до плоскости $\frac{x}{5} + \frac{y}{- 2} + \frac{z}{4} = 1$ .

Решение

По условию имеем уравнение плоскости в отрезках. Это значит, что необходимо привести его к нормальному уравнению плоскости. Для этого переходим к общему уравнению, после чего приведем к нормальному виду.

Получаем: $\frac{x}{5} + \frac{y}{- 2} + \frac{z}{4} = 1 \Leftrightarrow \frac{1}{5} x - \frac{1}{2} y + \frac{1}{4} z - 1 = 0$

Для вычисления нормирующего множителя применяем: $\frac{1}{\sqrt{{(\frac{1}{5})}^{2} + {(- \frac{1}{2})}^{2} + {(\frac{1}{4})}^{2}}} = \frac{1}{\sqrt{\frac{141}{25 \cdot 16}}} = \frac{20}{\sqrt{141}}$

Обе части уравнения $\frac{1}{5} x - \frac{1}{2} y + \frac{1}{4} z - 1 = 0$ умножаем на нормирующий множитель. Теперь получено нормальное уравнение исходной плоскости вида:

$\frac{4}{\sqrt{141}} x - \frac{10}{\sqrt{141}} y + \frac{5}{\sqrt{141}} z - \frac{20}{\sqrt{141}} = 0$

Отсюда видно, что $\cos α = \frac{4}{\sqrt{141}}, \cos β = - \frac{10}{\sqrt{141}}, \cos γ = \frac{5}{\sqrt{141}}, p = - \frac{20}{\sqrt{141}}, x_{0} = 5, y_{0} = - 1, z_{0} = 2$

Все имеющиеся данные помогут использовать формулу для нахождения искомого расстояния от точки до плоскости:

$p = |\cos α \cdot x_{0} + \cos β \cdot y_{0} + \cos γ \cdot z_{0} - p| = |\frac{4}{\sqrt{141}} \cdot 5 - \frac{10}{\sqrt{141}} \cdot (- 1) + \frac{5}{\sqrt{141}} \cdot 2 - \frac{20}{\sqrt{141}}| = \frac{20}{\sqrt{141}}$

Ответ: $\frac{20}{\sqrt{141}}$ .

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.