Нормальный вектор плоскости, координаты нормального вектора плоскости

Содержание:

05 апреля 2023
5 минут
6807

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.

Нормальный вектор плоскости – определение, примеры, иллюстрации

Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.

Определение 1

Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.

Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.

Нормальный вектор плоскости – определение, примеры, иллюстрации

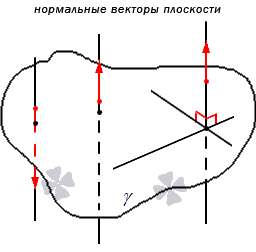
Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе $\vec{n}$ , расположенном в плоскости $γ$ , вектор $t \cdot \vec{n}$ , имея ненулевое значение параметра $t$ , также нормальный вектор плоскости $γ$ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.

Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.

Рассмотрим на примере нормального вектора на плоскости.

Задана прямоугольная система координат $О х у z$ в трехмерном пространстве. Координатные векторы $\vec{i}, \vec{j}, \vec{k}$ считаются нормальными векторами плоскостей $O y z, O x z$ и $O x y$ . Это суждение верно, так как $\vec{i}, \vec{j}, \vec{k}$ ненулевые и расположены на координатных прямых $O x, O y$ и $O z$ . Эти прямые перпендикулярны координатным плоскостям $O y z, O x z$ и $O x y$ .

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости

Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат $О х у z$ . Для определения нормального вектора $\vec{n} = (A, B, C)$ в плоскости необходимо наличие общего уравнения плоскости, имеющее вид $A x + B y + C z + D = 0$ . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.

Пример 1

Найти координаты нормального вектора, принадлежащего плоскости $\sqrt{2} x - 3 y + 7 z - 11 = 0$ .

Решение

По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что $\vec{n} = (\sqrt{2}, - 3, 7)$ - это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы $t \cdot \vec{n} = (\sqrt{2} \cdot t, - 3 \cdot t, 7 \cdot t)$ , t является любым действительным числом не равным нулю.

Ответ: $\vec{n} = (\sqrt{2}, - 3, 7)$ .

Пример 2

Определить координаты направляющих векторов заданной плоскости $x + 2 z - 7 = 0$ .

Решение

По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение $x + 2 z - 7 = 0$ к виду $1 \cdot x + 0 \cdot y + 2 z - 7 = 0$ . Отсюда получим, что координаты нормального вектора данной плоскости равны $(1, 0, 2)$ . Тогда множество векторов будет иметь такую форму записи $(t, 0, 2 \cdot t), t \in R, t \neq 0$ .

Ответ: $(t, 0, 2 \cdot t), t \in R, t \neq 0$ .

При помощи уравнения плоскости в отрезках, имеющего вид $\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$ , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны $(\frac{1}{a}, \frac{1}{b}, \frac{1}{c})$ .

Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.