- 16 июля 2025
- 8 минут
- 29 672
Нормальный вектор прямой, координаты нормального вектора прямой
Статью подготовили специалисты образовательного сервиса Zaochnik.
Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.
Нормальный вектор прямой – определение, примеры, иллюстрации
Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.
Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.
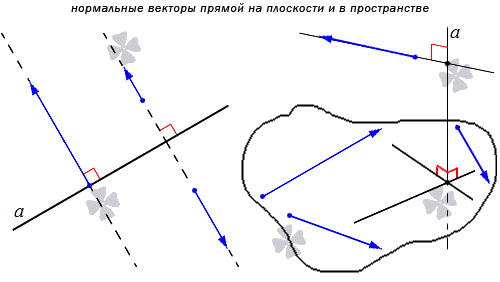
Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые и параллельные, а считается нормальным вектором прямой , также считается нормальным вектором для прямой . Когда прямая а имеет прямой вектор, тогда вектор является ненулевым при любом значении параметра, причем также является нормальным для прямой .
Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.
Если задана плоскость , то множеством векторов для является координатный вектор . Он считается ненулевым и принадлежащим координатной оси , перпендикулярной . Все множество нормальных векторов относительно можно записать, как .
Прямоугольная система имеет нормальный вектор , относящийся к прямой . Вектор также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный , считается нормальным для .
Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой
При рассмотрении прямоугольной системы координат выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.
Задана прямая вида _, найти координаты нормального вектора.
Решение
По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение .
Ответ: .
Бывают случаи, когда или из уравнения равняется нулю. Рассмотрим решение такого задания на примере.
Указать нормальный вектор для заданной прямой .
Решение
По условию нам дано общее уравнение прямой, значит запишем его таким образом . Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны .
Ответ: .
Если дано уравнение в отрезках вида или уравнение с угловым коэффициентом , тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.
Найти координаты нормального вектора, если дано уравнение прямой .
Решение
Для начала необходимо перейти от уравнения в отрезках к уравнению общего вида. Тогда получим, что .
Отсюда видно, что координаты нормального вектора имеют значение .
Ответ: .
Если прямая определена каноническим уравнением прямой на плоскости или параметрическим , тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут . Возможность нахождения координат нормального вектора возможно, благодаря условию перпендикулярности векторов и .
Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:
Для решения можно выбирать любой удобный способ.
Найти нормальный вектор заданной прямой .
Решение
Из прямой понятно, что направляющий вектор будет иметь координаты . Нормальный вектор заданной прямой является перпендикулярным .
Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов и запишем .
Значение – произвольное , следует найти . Если , отсюда получаем, что .
Значит, нормальный вектор имеет координаты .
Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем
Полученный результат координат нормального вектора равен .
Ответ: или .
Указать координаты нормального вектора прямой .
Решение
Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:
Отсюда видно, что координаты нормального вектора равны .
Ответ: .
Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат .
Когда прямая задается при помощи уравнений пересекающихся плоскостей и , тогда нормальный вектор плоскости относится к и , тогда получаем запись векторов в виде и .
Когда прямая определена при помощи канонического уравнения пространства, имеющего вид или параметрического, имеющего вид , отсюда и считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору . Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору .
Математические онлайн-калькуляторы




