- 16 июля 2025
- 6 минут
- 3 687
Прямая в пространстве – необходимые сведения
Статью подготовили специалисты образовательного сервиса Zaochnik.
Статья рассказывает о взаимном расположении линий в пространстве. Будут рассмотрены основные способы задания прямой с приведением примеров и наглядных рисунков.
Прямая в пространстве – понятие
Раздел о прямой на плоскости дает представление о течки и прямой. Расположение прямой в пространстве аналогично. Если мысленно отметить две точки и провести линию, соединив их, получим прямую, уходящую в бесконечность.
Точки, прямые и отрезки в пространстве обозначаются аналогично расположению в плоскости.
Если прямая располагается на плоскости в пространстве, тогда это можно подкрепить аксиомами:
- через две точки можно провести единственную прямую;
- если две точки прямой лежат в плоскости, то все остальные точки, расположенные на прямой принадлежат плоскости.
Имеет место аксиома, благодаря которой можно рассматривать прямую в пространстве в качестве двух пересеченных плоскостей:
Если две плоскости имеют общую точку, тогда имеют общую прямую, на которой лежат все общие точки этих плоскостей. Показано на рисунке, приведенном ниже.

Взаимное расположение прямых в пространстве
Прямые в пространстве могут совпадать, в таком случае они будут иметь большое количество общих точек или хотя бы.
Две прямые, расположенные в пространстве, могут пересекаться в случае наличия одной общей точки.
Данный случай говорит о том, что прямые располагаются на плоскости трехмерного пространства. Когда прямые, расположенные в пространстве, пересекаются, то переходим к определению угла между пересекающимися прямыми.

Две прямые пространства параллельны в том случае, если расположены в одной плоскости без общих точек.
Рассмотрим ниже расположение параллельных прямых.

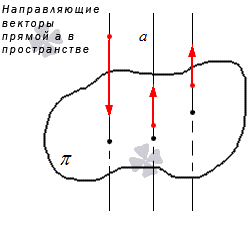
После рассмотрения определения параллельных прямых, расположенных в пространстве, необходимо добавить о направляющих векторах прямой.
Ненулевой вектор, который располагается на прямой или на параллельной ему прямой, называют направляющим вектором данной прямой.
Если по условию дана линия в пространстве, то он используется для решения задач.
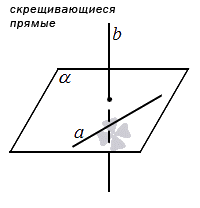
Две прямые пространства могут быть скрещивающимися.
Две прямые называют скрещивающимися, при условии, что они лежат в одной плоскости.
Это тесно связано с определением угла между скрещивающимися прямыми.
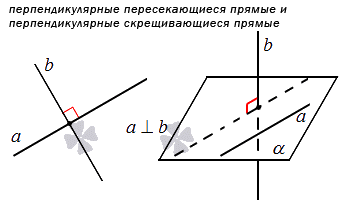
Особым случаем считается пересечение или скрещивание прямых под прямым углом в пространстве. Их называют перпендикулярными. Рассмотрим на рисунке.
Способы задания прямой в пространстве
Для того, чтобы расположить прямую в пространстве, существует несколько методов.
Из аксиомы для двух точек плоскости имеем, что через них может быть задана единственная прямая. При расположении двух точек в пространстве также задается только одна прямая, проходящая через них.
При прямоугольной системе координат прямая задается с помощью координат точек, которые располагаются в трехмерном пространстве. Это и позволяет составить уравнение прямой, проходящей через две заданные точки.
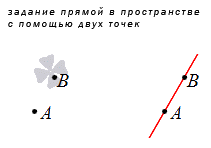
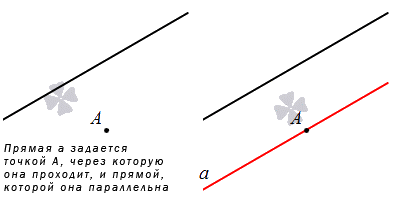
Еще один способ задания прямой – это теорема. Через любую точку пространства, не лежащую на данной прямой, может проходить прямая, параллельная данной, причем только одна.
Отсюда следует, что при задавании прямой и точки, не лежащей на ней, сможем определить прямую, которая параллельна заданной и проходит через указанную точку.
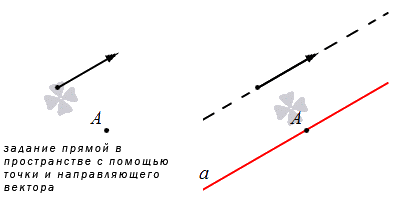
Есть способ, когда можно указать точку, направляющий вектор и прямую, которая проходит через нее. При задании прямой относительно прямоугольной систему координат, можно говорить о канонических и параметрических уравнениях прямой в пространстве.
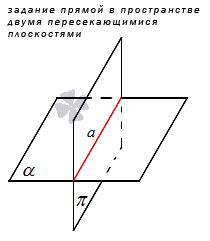
Немаловажный способ задания прямой – это способ, основанный на аксиоме: если две плоскости имеют общую точку, тогда имеют общую прямую, где располагаются общие точки заданных плоскостей. При задании двух пересекающихся плоскостей можно определить прямую пространства.
Если задана плоскость и нележащая в ней точка, тогда существует прямая, проходящая через нее и перпендикулярная заданной плоскости, причем только одна. Этот способ задания базируется на теореме. Получаем, что для определения прямой достаточно задать плоскость, перпендикулярную ей, с точкой, через которую проходит заданная прямая.
В случае, если прямая задается относительно введенной прямоугольной системы координат, то следует укрепить знания из статьиуравнения прямой, проходящей через заданную точку перпендикулярно в заданной плоскости.Рассмотрим задание прямой, используя точку, через которую она пройдет, и плоскости, которая располагается перпендикулярно относительно заданной прямой.

Математические онлайн-калькуляторы




