- 16 июля 2025
- 10 минут
- 24 629
Проекция точки на плоскость, координаты проекции точки на плоскость
Статью подготовили специалисты образовательного сервиса Zaochnik.
В этой статье мы найдем ответы на вопросы о том, как создать проекцию точки на плоскость и как определить координаты этой проекции. Опираться в теоретической части будем на понятие проецирования. Дадим определения терминам, сопроводим информацию иллюстрациями. Закрепим полученные знания при решении примеров.
Проецирование, виды проецирования
Для удобства рассмотрения пространственных фигур используют чертежи с изображением этих фигур.
Проекция фигуры на плоскость – чертеж пространственной фигуры.
Очевидно, что для построения проекции существует ряд используемых правил.
Проецирование – процесс построения чертежа пространственной фигуры на плоскости с использованием правил построения.
Плоскость проекции - это плоскость, в которой строится изображение.
Использование тех или иных правил определяет тип проецирования: центральное или параллельное.
Частным случаем параллельного проецирования является перпендикулярное проецирование или ортогональное: в геометрии в основном используют именно его. По этой причине в речи само прилагательное «перпендикулярное» часто опускают: в геометрии говорят просто «проекция фигуры» и подразумевают под этим построение проекции методом перпендикулярного проецирования. В частных случаях, конечно, может быть оговорено иное.
Отметим тот факт, что проекция фигуры на плоскость по сути есть проекция всех точек этой фигуры. Поэтому, чтобы иметь возможность изучать пространственную фигуру на чертеже, необходимо получить базовый навык проецировать точку на плоскость. О чем и будем говорить ниже.
Проекция точки на плоскость
Напомним, что чаще всего в геометрии, говоря о проекции на плоскость, имеют в виду применение перпендикулярной проекции.
Произведем построения, которые дадут нам возможность получить определение проекции точки на плоскость.
Допустим, задано трехмерное пространство, а в нем - плоскость α и точка , не принадлежащая плоскости . Начертим через заданную точку прямую а перпендикулярно заданной плоскости . Точку пересечения прямой и плоскости обозначим как она по построению будет служить основанием перпендикуляра, опущенного из точки на плоскость . 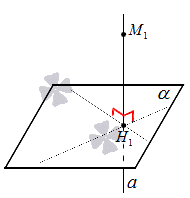
В случае, если задана точка , принадлежащая заданной плоскости , то будет служить проекцией самой себя на плоскость .
Проекция точки на плоскость – это либо сама точка (если она принадлежит заданной плоскости), либо основание перпендикуляра, опущенного из заданной точки на заданную плоскость.
Нахождение координат проекции точки на плоскость, примеры
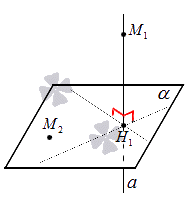
Пускай в трехмерном пространстве заданы: прямоугольная система координат , плоскость , точка . Необходимо найти координаты проекции точки на заданную плоскость.
Решение очевидным образом следует из данного выше определения проекции точки на плоскость.
Обозначим проекцию точки на плоскость как . Согласно определению, является точкой пересечения данной плоскости и прямой , проведенной через точку (перпендикулярной плоскости). Т.е. необходимые нам координаты проекции точки – это координаты точки пересечения прямой и плоскости .
Таким образом, для нахождения координат проекции точки на плоскость необходимо:
- получить уравнение плоскости (в случае, если оно не задано). Здесь вам поможет статья о видах уравнений плоскости;
- определить уравнение прямой , проходящей через точку и перпендикулярной плоскости (изучите тему об уравнении прямой, проходящей через заданную точку перпендикулярно к заданной плоскости);
- найти координаты точки пересечения прямой и плоскости (статья – нахождение координат точки пересечения плоскости и прямой). Полученные данные и будут являться нужными нам координатами проекции точки на плоскость .
Рассмотрим теорию на практических примерах.
Определите координаты проекции точки на плоскость .
Решение
Как мы видим, уравнение плоскости нам задано, т.е. составлять его необходимости нет.
Запишем канонические уравнения прямой , проходящей через точку и перпендикулярной заданной плоскости. В этих целях определим координаты направляющего вектора прямой . Поскольку прямая а перпендикулярна заданной плоскости, то направляющий вектор прямой – это нормальный вектор плоскости . Таким образом,
Теперь составим канонические уравнения прямой в пространстве, проходящей через точку и имеющей направляющий вектор
Для нахождения искомых координат следующим шагом определим координаты точки пересечения прямой и плоскости . В этих целях переходим от канонических уравнений к уравнениям двух пересекающихся плоскостей:
Составим систему уравнений:
И решим ее, используя метод Крамера:
Таким образом, искомые координаты заданной точки на заданную плоскость будут: .
Ответ: .
В прямоугольной системе координат трехмерного пространства даны точки и М1(-1, -2, 5). Необходимо найти координаты проекции на плоскость
Решение
В первую очередь запишем уравнение плоскости, проходящей через три заданные точки:
Далее рассмотрим еще один вариант решения, отличный от того, что мы использовали в первом примере.
Запишем параметрические уравнения прямой , которая будет проходить через точку перпендикулярно плоскости . Плоскость имеет нормальный вектор с координатами , т.е. вектор
Теперь, имея координаты точки прямой и координаты направляющего вектора этой прямой, запишем параметрические уравнения прямой в пространстве:
Затем определим координаты точки пересечения плоскости и прямой
Для этого в уравнение плоскости подставим:
Теперь по параметрическим уравнениям найдем значения переменных и при :
Таким образом, проекция точки на плоскость будет иметь координаты .
Ответ: .
Отдельно остановимся на вопросе нахождения координат проекции точки на координатные плоскости и плоскости, которые параллельны координатным плоскостям.
Пусть задана точки и координатные плоскости и . Координатами проекции этой точки на данные плоскости будут соответственно: и . Рассмотрим также плоскости, параллельные заданным координатным плоскостям:
И проекциями заданной точки на эти плоскости будут точки с координатами и .
Продемонстрируем, как был получен этот результат.
В качестве примера определим проекцию точки на плоскость . Остальные случаи – по аналогии.
Заданная плоскость параллельна координатной плоскости и является ее нормальным вектором. Этот же вектор служит направляющим вектором прямой, перпендикулярной к плоскости . Тогда параметрические уравнения прямой, проведенной через точку и перпендикулярной заданной плоскости, будут иметь вид:
Найдем координаты точки пересечения этой прямой и заданной плоскости. Подставим сначала в уравнение равенства: и получим:
Затем вычислим искомые координаты, используя параметрические уравнения прямой при :
Т.е., проекцией точки на плоскость будет являться точка с координатами .
Необходимо определить координаты проекции точки на координатную плоскость и на плоскость .
Решение
Координатной плоскости будет соответствовать неполное общее уравнение плоскости . Проекция точки на плоскость будет иметь координаты .
Уравнение плоскости возможно записать как . Теперь просто записать координаты проекции точки на плоскость :
Ответ: и
Математические онлайн-калькуляторы




