Проекция точки на прямую, координаты проекции точки на прямую

Содержание:

Данная статья рассматривает понятие проекции точки на прямую (ось). Мы дадим ему определение с использованием поясняющего рисунка; изучим способ определения координат проекции точки на прямую (на плоскости или в трехмерном пространстве); разберем примеры.

Проекция точки на прямую, определение

В статье «Проекция точки на плоскость, координаты» мы упоминали, что проецирование фигуры является обобщенным понятием перпендикулярного или ортогонального проецирования.

Все геометрические фигуры состоят из точек, соответственно проекция этой фигуры есть множество проекций всех ее точек. Поэтому, чтобы иметь возможность спроецировать фигуру на прямую, необходимо получить навык проецирования точки на прямую.

Определение 1

Проекция точки на прямую – это или сама точка, если она принадлежит заданной прямой, или основание перпендикуляра, опущенного из этой точки на заданную прямую.

Рассмотрим рисунок ниже: точка $H_{1}$ служит проекцией точки $М_{1}$ на прямую $a$ , а точка $М_{2}$ , принадлежащая прямой, является проекцией сама себя.

Проекция точки на прямую, определение

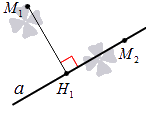
Данное определение верно для случая на плоскости и в трехмерном пространстве.

Чтобы на плоскости получить проекцию точки $М_{1}$ на прямую $a$ , проводится прямая $b$ , проходящая через заданную точку $M_{1}$ и перпендикулярная прямой $a$ . Таким образом, точка пересечения прямых $a$ и $b$ будет проекцией точки $М 1$ на прямую $a .$

Проекция точки на прямую, определение

В трехмерном пространстве проекцией точки на прямую будет служить точка пересечения прямой $a$ и плоскости $α$ , проходящей через точку $М_{1}$ и перпендикулярной прямой $a$ .

Проекция точки на прямую, определение

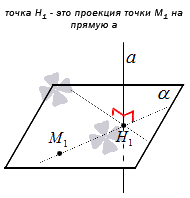
Нахождение координат проекции точки на прямую

Рассмотрим данный вопрос в случаях проецирования на плоскости и в трехмерном пространстве.

Пусть нам заданы прямоугольная система координат $O x y$ , точка $М_{1} (x_{1}, y_{1})$ и прямая $a$ . Необходимо найти координаты проекции точки $М_{1}$ на прямую $a$ .

Проложим через заданную точку $М_{1} (x_{1}, y_{1})$ прямую $b$ перпендикулярно прямой $a$ . Точку пересечения маркируем как $H_{1}$ . Точка $Н_{1}$ будет являться точкой проекции точки $М_{1}$ на прямую $a$ .

Из описанного построения можно сформулировать алгоритм, который позволяет находить координаты проекции точки $М 1 (x 1, y 1)$ на прямую $a$ :

- составляем уравнение прямой (если оно не задано). Для совершения этого действия необходим навык составления основных уравнений на плоскости;

- записываем уравнение прямой $b$ (проходящей через точку $М_{1}$ и перпендикулярной прямой $a$ ). Здесь поможет статья об уравнении прямой, проходящей через заданную точку перпендикулярно заданной прямой;

- определяем искомые координаты проекции как координаты точки пересечения прямых $a$ и $b$ . Для этого решаем систему уравнений, составляющие которой – уравнения прямых $a$ и $b$ .

Пример 1

На плоскости $O x y$ заданы точки $М_{1} (1, 0)$ и прямая $a$ (общее уравнение $- 3 x + y + 7 = 0$ ). Необходимо определить координаты проекции точки $М_{1}$ на прямую $a$ .

Решение

Уравнение заданной прямой известно, поэтому, согласно алгоритму, переходим к шагу записи уравнения прямой $b$ . Прямая $b$ перпендикулярна прямой $a$ , а значит нормальный вектор прямой $a$ служит направляющим вектором прямой $b$ . Тогда направляющий вектор прямой $b$ запишем как $\vec{b} = (3, 1)$ . Запишем и каноническое уравнение прямой $b$ , поскольку нам также заданы координаты точки $М_{1}$ , через которую проходит прямая $b$ :

$\frac{x - 1}{3} = \frac{y}{1}$

Заключительным шагом определяем координаты точки пересечения прямых $a$ и $b$ . Перейдем от канонических уравнений прямой $b$ к общему ее уравнению:

$\frac{x - 1}{3} = \frac{y}{1} \Leftrightarrow 1 \cdot (x - 1) = 3 \cdot y \Leftrightarrow x - 3 y - 1 = 0$

Составим систему уравнений из общих уравнений прямых $a$ и $b$ и решим ее:

$\{\begin{cases} 3 x + y + 7 = 0 \\ x - 3 y - 1 = 0 \end{cases} \Leftrightarrow \{\begin{cases} y = - 3 x - 7 \\ x - 3 y - 1 = 0 \end{cases} \Leftrightarrow \{\begin{cases} y = - 3 x - 7 \\ x - 3 \cdot (- 3 x - 7) - 1 = 0 \end{cases} \Leftrightarrow \Leftrightarrow \{\begin{cases} y = - 3 x - 7 \\ x = - 2 \end{cases} \Leftrightarrow \{\begin{cases} y = - 3 \cdot (- 2) - 7 \\ x = - 2 \end{cases} \Leftrightarrow \{\begin{cases} y = - 1 \\ x = - 2 \end{cases}$

В конечном итоге мы получили координаты проекции точки $М_{1} (1, 0)$ на прямую $3 x + y + 7 = 0 : (- 2, - 1)$ .

Ответ: $(- 2, - 1)$ .

Подробнее рассмотрим случай, когда необходимо определить координаты проекции заданной точки на координатные прямые и параллельные им прямые.

Пусть заданы координатные прямые $O x$ и $O y$ , а также точка $М_{1} (x_{1}, y_{1})$ . Понятно, что проекцией заданной точки на координатную прямую $O x$ вида $y = 0$ будет точка с координатами $(x_{1}, 0)$ . Так и проекция заданной точки на координатную прямую $O y$ будет иметь координаты $(0, y_{1})$ .

Любую произвольную прямую, параллельную оси абсцисс, возможно задать неполным общим уравнением $B y + C = 0 \Leftrightarrow y = - \frac{C}{B}$ , а прямую, параллельную оси ординат - $A x + C = 0 \Leftrightarrow x = - \frac{C}{A.}$

Тогда проекциями точки $М_{1} (x_{1}, y_{1})$ на прямые $y = - \frac{C}{B}$ и $x = - \frac{C}{A}$ станут точки с координатами $(x_{1}, - \frac{C}{B})$ и $(- \frac{C}{A}, y_{1})$ .

Пример 2

Определите координаты проекции точки $М_{1} (7, - 5)$ на координатную прямую $O y$ , а также на прямую, параллельную прямой $O y$ $2 y - \sqrt{3} = 0$ .

Решение

Запишем координаты проекции заданной точки на прямую $O y : (0, - 5)$ .

Запишем уравнение прямой $2 y - \sqrt{3} = 0$ в виде $y = \frac{\sqrt{3}}{2}$ . Становится видно, что проекция заданной точки на прямую $y = \frac{\sqrt{3}}{2}$ будет иметь координаты $(7, \frac{\sqrt{3}}{2})$ .

Ответ: $(0, - 5)$ и $(7, \frac{\sqrt{3}}{2})$ .

Пусть в трехмерном пространстве заданы прямоугольная система координат $O x y z$ , точка $М_{1} (x_{1}, y_{1}, z_{1})$ и прямая $a$ . Найдем координаты проекции точки $М_{1}$ на прямую $a$ .

Построим плоскость $α$ , проходящую через точку $М_{1}$ и перпендикулярную прямой $a$ . Проекцией заданной точки на прямую $a$ станет точка пересечения прямой $a$ и плоскости $α$ . Исходя из этого, приведем алгоритм для нахождения координат проекции точки $М_{1} (x_{1}, y_{1}, z_{1})$ на прямую $a$ :

- запишем уравнение прямой а (если оно не задано). Для решения этой задачи необходимо ознакомиться со статьей об уравнениях прямой в пространстве;

- составим уравнение плоскости $α$ , проходящей через точку $М_{1}$ и перпендикулярной прямой $a$ (см. статью «Уравнение плоскости, проходящей через заданную точку перпендикулярно заданной прямой»);

- найдем искомые координаты проекции точки $М_{1} (x_{1}, y_{1}, z_{1})$ на прямую $a$ – это будут координаты точки пересечения прямой $α$ и плоскости $α$ (в помощь – статья «Координаты точки пересечения прямой и плоскости»).

Пример 3

Задана прямоугольная система координат $O x y z$ , и в ней – точка $М_{1} (0, 1, - 1)$ и прямая $a$ . Прямой $a$ соответствуют канонические уравнения вида: $\frac{x + 2}{3} = \frac{y - 6}{- 4} = \frac{z + 1}{1}$ . Определите координаты проекции точки $М_{1}$ на прямую $a$ .

Решение

Используем указанный выше алгоритм. Уравнения прямой $a$ известны, поэтому первый шаг алгоритма пропускаем. Запишем уравнение плоскости $α$ . Для этого определим координаты нормального вектора плоскости $α$ . Из заданных канонических уравнений прямой $a$ выделим координаты направляющего вектора этой прямой: $(3, - 4, 1)$ , который будет являться нормальным вектором плоскости $α$ , перпендикулярной прямой $a$ . Тогда $\vec{n} = (3, - 4, 1)$ – нормальный вектор плоскости $α$ . Таким образом, уравнение плоскости $α$ будет иметь вид:

$3 \cdot (x - 0) - 4 \cdot (y - 1) + 1 \cdot (z - (- 1)) = 0 \Leftrightarrow 3 x - 4 y + z + 5 = 0$

Теперь найдем координаты точки пересечения прямой а и плоскости α, для этого используем два способа:

Заданные канонические уравнения позволяют получить уравнения двух пересекающихся плоскостей, определяющих прямую $a$ :

$\frac{x + 2}{3} = \frac{y - 6}{- 4} = \frac{z + 1}{1} \Leftrightarrow \{\begin{cases} \begin{array}{l} - 4 \cdot (x + 2) = 3 \cdot (y - 6) \\ 1 \cdot (x + 2) = 3 \cdot (z + 1) \end{array} \\ 1 \cdot (y - 6) = - 4 \cdot (z + 1) \end{cases} \Leftrightarrow \{\begin{cases} 4 x + 3 y - 10 = 0 \\ x - 3 z - 1 = 0 \end{cases}$

Чтобы найти точки пересечения прямой $\{\begin{cases} 4 x + 3 y - 10 = 0 \\ x - 3 z - 1 = 0 \end{cases}$ и плоскости $3 x - 4 y + z + 5 = 0$ , решим систему уравнений:

$\{\begin{cases} \begin{array}{l} 4 x + 3 y - 10 = 0 \\ x - 3 z - 1 = 0 \end{array} \\ 3 x - 4 y + z + 5 = 0 \end{cases} \Leftrightarrow \{\begin{cases} \begin{array}{l} 4 x + 3 y = 10 \\ x - 3 z = 1 \end{array} \\ 3 x - 4 y + z = - 5 \end{cases}$

В данном случае используем метод Крамера, но возможно применить любой удобный:

$∆ = |\begin{matrix} 4 & 3 & 0 \\ 1 & 0 & - 3 \\ 3 & - 4 & 1 \end{matrix}| = - 78 ∆_{x} = |\begin{matrix} 10 & 3 & 0 \\ 1 & 0 & - 3 \\ - 5 & - 4 & 1 \end{matrix}| = - 78 \Rightarrow x = \frac{∆_{x}}{∆} = \frac{- 78}{- 78} = 1 ∆_{y} = |\begin{matrix} 4 & 10 & 0 \\ 1 & 1 & - 3 \\ 3 & - 5 & 1 \end{matrix}| = - 156 \Rightarrow y = \frac{∆_{y}}{∆} = \frac{- 156}{- 78} = 2 ∆_{z} = |\begin{matrix} 4 & 3 & 10 \\ 1 & 0 & 1 \\ 3 & - 4 & - 5 \end{matrix}| = 0 \Rightarrow z = \frac{∆_{z}}{∆} = \frac{0}{- 78} = 0$

Таким образом, проекцией заданной точки на прямую $a$ является точка $c$ координатами $(1, 2, 0)$

На основе заданных канонических уравнений легко записать параметрические уравнения прямой в пространстве:

$\frac{x + 2}{3} = \frac{y - 6}{- 4} = \frac{z + 1}{1} \Leftrightarrow \{\begin{cases} \begin{array}{l} x = - 2 + 3 \cdot λ \\ y = 6 - 4 \cdot λ \end{array} \\ z = - 1 + λ \end{cases}$

Подставим в уравнение плоскости, имеющее вид $3 x - 4 y + z + 5 = 0$ , вместо $x, y$ и $z$ их выражения через параметр:

$3 \cdot (- 2 + 3 \cdot λ) - 4 \cdot (6 - 4 \cdot λ) + (- 1 + λ) + 5 = 0 \Leftrightarrow 26 \cdot λ = 0 \Leftrightarrow λ = 1$

Вычислим искомые координаты точки пересечения прямой $a$ и плоскости $α$ по параметрическим уравнениям прямой $a$ при $λ = 1$ :

$\{\begin{cases} \begin{array}{l} x = - 2 + 3 \cdot 1 \\ y = 6 - 4 \cdot 1 \end{array} \\ z = - 1 + 1 \end{cases} \Leftrightarrow \{\begin{cases} \begin{array}{l} x = 1 \\ y = 2 \end{array} \\ z = 0 \end{cases}$

Таким образом, проекция заданной точки на прямую $a$ имеет координаты $(1, 2, 0)$

Ответ: $(1, 2, 0)$

Напоследок отметим, что проекциями точки $М_{1} (x_{1}, y_{1}, z_{1})$ на координатные прямые $O x, O y$ и $O z$ буду являться точки с координатами $(x_{1}, 0, 0), (0, y_{1}, 0)$ и $(0, 0, z_{1})$ соответственно.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта