- 16 июля 2025
- 9 минут
- 25 947
Расстояние между двумя параллельными прямыми: определение и примеры нахождения
Статью подготовили специалисты образовательного сервиса Zaochnik.
В материале этой статьи разберем вопрос нахождения расстояния между двумя параллельными прямыми, в частности, при помощи метода координат. Разбор типовых примеров поможет закрепить полученные теоретические знания.
Расстояние между двумя параллельными прямыми: определение
Расстояние между двумя параллельными прямыми – это расстояние от некоторой произвольной точки одной из параллельных прямых до другой прямой.
Приведем иллюстрацию для наглядности: 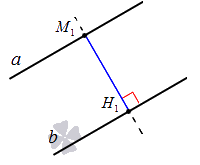
На чертеже изображены две параллельные прямые и . Точка принадлежит прямой , из нее опущен перпендикуляр на прямую . Полученный отрезок и есть расстояние между двумя параллельными прямыми и .
Указанное определение расстояния между двумя параллельными прямыми справедливо как на плоскости, так и для прямых в трехмерном пространстве. Кроме того, данное определение взаимосвязано со следующей теоремой.
Когда две прямые параллельны, все точки одной из них равноудалены от другой прямой.
Пусть нам заданы две параллельные прямые и . Зададим на прямой а точки и , опустим из них перпендикуляры на прямую , обозначив их основания соответственно как и . – это расстояние между двумя параллельными прямыми по определению, и нам необходимо доказать, что .
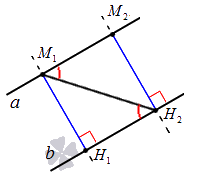
Пусть будет также существовать некоторая секущая, которая пересекает две заданные параллельные прямые. Условие параллельности прямых, рассмотренное в соответствующей статье, дает нам право утверждать, что в данном случае внутренние накрест лежащие углы, образованные при пересечении секущей заданных прямых, являются равными: . Прямая перпендикулярна прямой по построению, и, конечно, перпендикулярна прямой . Получившиеся треугольники и являются прямоугольными и равными друг другу по гипотенузе и острому углу: – общая гипотенуза, . Опираясь на равенство треугольников, мы можем говорить о равенстве их сторон, т.е.: . Теорема доказана.
Отметим, что расстояние между двумя параллельными прямыми – наименьшее из расстояний от точек одной прямой до точек другой.
Нахождение расстояния между параллельными прямыми
Мы уже выяснили, что, по сути, чтобы найти расстояние между двумя параллельными прямыми, необходимо определить длину перпендикуляра, опущенного из некой точки одной прямой на другую. Способов, как это сделать, несколько. В каких-то задачах удобно воспользоваться теоремой Пифагора; другие предполагают использование признаков равенства или подобия треугольников и т.п. В случаях, когда прямые заданы в прямоугольной системе координат, возможно вычислить расстояние между двумя параллельными прямыми, используя метод координат. Рассмотрим его подробнее.
Зададим условия. Допустим, зафиксирована прямоугольная система координат, в которой заданы две параллельные прямые и . Необходимо определить расстояние между заданными прямыми.
Решение задачи построим на определении расстояния между параллельными прямыми: для нахождения расстояния между двумя заданными параллельными прямыми необходимо:
- найти координаты некоторой точки , принадлежащей одной из заданных прямых;
- произвести вычисление расстояния от точки до заданной прямой, которой эта точка не принадлежит.
Опираясь на навыки работы с уравнениями прямой на плоскости или в пространстве, определить координаты точки просто. При нахождении расстояния от точки до прямой пригодится материал статьи о нахождении расстояния от точки до прямой.
Вернемся к примеру. Пусть прямая описывается общим уравнением , а прямая – уравнением . Тогда расстояние между двумя заданными параллельными прямыми возможно вычислить, используя формулу:
Выведем эту формулу.
Используем некоторую точку , принадлежащую прямой . В таком случае координаты точки будут удовлетворять уравнению . Таким образом, справедливым является равенство: ; из него получим: .
Когда , нормальное уравнение прямой b будет иметь вид:
При нормальное уравнение прямой b будет выглядеть так:
И тогда для случаев, когда , применима формула: .
А для искомое расстояние определяется по формуле
Таким образом, при любом значении числа длина отрезка (от точки до прямой ) вычисляется по формуле:
Выше мы получили: , тогда можем преобразовать формулу: . Так мы, собственно, получили формулу, указанную в алгоритме метода координат.
Разберем теорию на примерах.
Заданы две параллельные прямые и . Необходимо определить расстояние между ними.
Решение
Исходные параметрические уравнения дают возможность задать координаты точки, через которую проходит прямая, описываемая параметрическими уравнениями. Таким образом, получаем точку . Требуемое расстояние – это расстояние между точкой до прямой , произведем его вычисление.
Заданное уравнение прямой с угловым коэффициентом преобразуем в нормальное уравнение прямой. С этой целью сначала осуществим переход к общему уравнению прямой:
Вычислим нормирующий множитель: . Умножим на него обе части последнего уравнения и, наконец, получим возможность записать нормальное уравнение прямой: .
При , а вычислим искомое расстояние как модуль значения крайнего равенства:
Ответ: .
В фиксированной прямоугольной системе координат заданы две параллельные прямые, определяемые уравнениями и . Необходимо найти расстояние между заданными параллельными прямыми.
Решение
Условиями задачи определено одно общее уравнение, задаваемое одну из исходных прямых: x-3=0. Преобразуем исходное каноническое уравнение в общее: . При переменной x коэффициенты в обоих уравнениях равны (также равны и при – нулю), а потому имеем возможность применить формулу для нахождения расстояния между параллельными прямыми:
Ответ: .
Напоследок рассмотрим задачу на нахождение расстояния между двумя параллельными прямыми в трехмерном пространстве.
В прямоугольной системе координат заданы две параллельные прямые, описываемые каноническими уравнениями прямой в пространстве: и . Необходимо найти расстояние между этими прямыми.
Решение
Из уравнения легко определются координаты точки, через которую проходит прямая, описываемая этим уравнением: . Произведем вычисление расстояния от точки до прямой .
Вычислим векторное произведение векторов :
Применим формулу расчета расстояния от точки до прямой в пространстве:
Ответ: .
Математические онлайн-калькуляторы




