Расстояние между прямой и параллельной ей плоскостью: определение и примеры нахождения

Содержание:

16 июля 2023
6 минут
2437

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

В статье ниже мы найдем определение, что же представляет собой расстояние между прямой и плоскостью, параллельными друг другу; разберем способ определить это расстояние и применим полученный навык в решении конкретных задач.

Расстояние между прямой и параллельной ей плоскостью: определение

Определение 1

Расстояние между прямой и параллельной ей плоскостью – это расстояние от любой точки заданной прямой до заданной плоскости.

Пусть нам даны прямая $a$ и плоскость $ϒ_{1}$ , ей параллельная. Используем некоторую точку $М_{1}$ , принадлежащую прямой $a$ : проведем перпендикуляр из этой точки на заданную плоскость. Основание перпендикуляра на плоскости обозначим как $Н_{1}$ . Длина перпендикуляра $М_{1} Н_{1}$ и будет являться расстоянием между исходными параллельными прямой и плоскостью.

Расстояние между прямой и параллельной ей плоскостью: определение

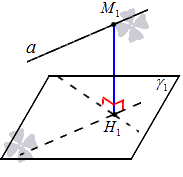
Указанное определение имеет тесную взаимосвязь со следующей теоремой.

Теорема N

Когда прямая $a$ параллельна плоскости $ϒ_{1}$ , все точки прямой $a$ находятся на одинаковом расстоянии от плоскости $ϒ_{1}$ .

Доказательство N

Используем любую произвольную точку на прямой $a$ – проведем через нее плоскость $ϒ_{2}$ , параллельную заданной плоскости $ϒ_{1}$ . В таком построении прямая а принадлежит плоскости $ϒ_{2}$ (в ином случае прямая а пересекала бы эту плоскость, а, следовательно, пересекала бы и плоскость $ϒ_{1}$ , что противоречит исходному условию). В статье, которая разбирает тему расстояния между параллельными плоскостями, мы доказали теорему о том, что все точки одной из параллельных плоскостей равноудалены от точек другой плоскости. Таким образом, все точки прямой $a$ , принадлежащей плоскости $ϒ_{2}$ (в свою очередь, параллельной плоскости $ϒ_{1}$ ) находятся на одинаковом расстоянии от плоскости $ϒ_{1}$ . Что и требовалось доказать.

Нахождение расстояния между параллельными прямой и плоскостью

Искомое расстояние между параллельными прямой и плоскостью обычно находится с использованием теоремы Пифагора, признаков равенства или подобия треугольников и пр.

Если же в трехмерном пространстве задана прямоугольная система координат, мы можем применить метод координат. Разберем его подробнее.

Допустим, в трехмерном пространстве зафиксирована некоторая прямоугольная система координат $O x y z$ , в которой заданы прямая $a$ и плоскость $ϒ_{1}$ , параллельные между собой. Требуется определить расстояние между заданными прямой и плоскостью.

Построим решение этой задачи на указанном выше определении расстояния между прямой и параллельной ей плоскостью.

Используем некоторую точку $М_{1}$ , принадлежащую прямой $a$ : расстояние от этой точки до заданной плоскости и будет являться искомым расстоянием между параллельными прямой и плоскостью. Определим координаты точки $М_{1}$ как $(x_{1}, y_{1}, z_{1})$ и запишем нормальное уравнение плоскости $ϒ_{1}$ : $\cos α \cdot x + \cos β \cdot y + \cos γ \cdot z - p = 0$ . Теперь мы можем вычислить искомое расстояние, для чего применим формулу:

$|M_{1} H_{1}| = |\cos α \cdot x_{1} + \cos β \cdot y_{1} + \cos γ \cdot z_{1} - p|$

Вывод этой формулы можно изучить в статье о нахождении расстояния от точки до плоскости.

Таким образом, мы можем сформулировать алгоритм для нахождения расстояния между прямой и параллельной ей плоскостью:

- определяем координаты точки, принадлежащей заданной прямой (для этого пригодятся навыки работы с основными видами уравнений в пространстве);

- записываем нормальное уравнение заданной плоскости вида $\cos α \cdot x + \cos β \cdot y + \cos γ \cdot z - p = 0$ (чтобы легко справиться с этим пунктом, следует повторить материал по основным видам уравнений плоскости и вспомнить навык приведения уравнения плоскости к нормальному виду);

- вычисляем искомое расстояние по формуле: $|M_{1} H_{1}| = |\cos α \cdot x_{1} + \cos β \cdot y_{1} + \cos γ \cdot z_{1} - p|$

Пример 1

Задана прямая $\frac{x - 1}{2} = \frac{y}{0} = \frac{z + 1}{1}$ и параллельная ей плоскость $3 x + 2 y - 6 z - 2 = 0$ . Необходимо определить расстояние между ними.

Решение

Заданные условием задачи канонические уравнения прямой $\frac{x - 1}{2} = \frac{y}{0} = \frac{z + 1}{1}$ дают возможность определить точку $М_{1} (1, 0, - 1)$ , принадлежащую этой прямой.

Запишем нормальное уравнение исходной плоскости, т.е. преобразуем заданное условием задачи общее уравнение в нормальный вид. Вычислим нормирующий множитель: $\frac{1}{\sqrt{3^{2} + 2^{2} + (- 6)^{2}}} = \frac{1}{7}$ и умножим на него обе части исходного общего уравнения плоскости:

$3 x + 2 y - 6 z - 2 = 0 \Leftrightarrow \frac{1}{7} \cdot (3 x + 2 y - 6 z - 2) = \frac{1}{7} \cdot 0 \Leftrightarrow \frac{3}{7} x + \frac{2}{7} y - \frac{6}{7} z - \frac{2}{7}$

Теперь можем вычислить требуемое расстояние как расстояние от точки $М_{1}$ до плоскости $\frac{3}{7} x + \frac{2}{7} y - \frac{6}{7} z - \frac{2}{7} = 0$ :

$|M_{1} H_{1}| = |\frac{3}{7} \cdot 1 + \frac{2}{7} \cdot 0 - \frac{6}{7} \cdot (- 1) - \frac{2}{7}| = 1$

Ответ: $1$ .

Пример 2

Заданы прямая $\{\begin{cases} 2 x - y + 9 = 0 \\ 2 x + y - 2 z + 3 = 0 \end{cases}$ и параллельная ей плоскость $\frac{x}{- \frac{3}{2}} + \frac{y}{\frac{3}{2}} + \frac{z}{- 3} = 1$ . Необходимо найти расстояние между ними.

Решение

Условием задачи прямая описывается уравнениями двух пересекающихся плоскостей. Определим координаты $(x_{1}, y_{1}, z_{1})$ некой точки $М_{1}$ , принадлежащей этой прямой. Искомые координаты должны отвечать условиям уравнений прямой, т.е. координаты $(x_{1}, y_{1}, z_{1})$ будут частным решением системы линейных уравнений $\{\begin{cases} 2 x - y + 9 = 0 \\ 2 x + y - 2 z + 3 = 0 \end{cases}$ . Найдем частное решение этой системы.

Примем $z = 0$ , тогда получим: $\{\begin{cases} 2 x - y = - 9 \\ 2 x + y = - 3 \end{cases}$ , откуда $x = - 3, y = 3$ .

Таким образом, координаты точки $М_{1}$ равны $(- 3, 3, 0)$ .

Теперь запишем нормальное уравнение плоскости, заданной условием задачи уравнением плоскости в отрезках. Сначала осуществим переход к общему уравнению плоскости:

$\frac{x}{- \frac{3}{2}} + \frac{y}{\frac{3}{2}} + \frac{z}{- 2} = 1 \Leftrightarrow - \frac{2}{3} x + \frac{2}{3} y - \frac{1}{3} z - 1 = 0$

Полученное общее уравнение уже является нормальным уравнением плоскости, поэтому в дальнейших преобразованиях необходимости нет.

Наконец, вычислим расстояние от точки до плоскости, которое и будет являться требуемым расстоянием от заданной прямой к заданной плоскости:

$|M_{1} H_{1}| = |- \frac{2}{3} \cdot (- 3) + \frac{2}{3} \cdot 3 - \frac{1}{3} \cdot 0 - 1 = 0| = 3$

Ответ: $3$ .

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.