Расстояние от точки до плоскости: определение и примеры нахождения

Содержание:

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Данная статья рассказывает об определении расстояния от точки до плоскости. произведем разбор методом координат, который позволит находить расстояние от заданной точки трехмерного пространства. Для закрепления рассмотрим примеры нескольких задач.

Расстояние от точки до плоскости – определение

Расстояние от точки до плоскости находится посредством известного расстояния от точки до точки, где одна из них заданная, а другая – проекция на заданную плоскость.

Когда в пространстве задается точка $М_{1}$ с плоскостью $χ$ , то через точку можно провести перпендикулярную плоскости прямую. $Н_{1}$ является общей точкой их пересечения. Отсюда получаем, что отрезок $М_{1} Н_{1}$ – это перпендикуляр, который провели из точки $М_{1}$ к плоскости $χ$ , где точка $Н_{1}$ – основание перпендикуляра.

Определение 1

Расстоянием от точки до плоскости называют расстояние от заданной точки к основанию перпендикуляра, который провели из заданной точки к заданной плоскости.

Определение может быть записано разными формулировками.

Определение 2

Расстоянием от точки до плоскости называют длину перпендикуляра, который провели из заданной точки к заданной плоскости.

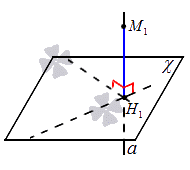
Расстояние от точки до плоскости – определение

Расстояние от точки $М_{1}$ к плоскости $χ$ определяется так: расстояние от точки $М_{1}$ до плоскости $χ$ будет являться наименьшим от заданной точки до любой точки плоскости. Если точка $Н_{2}$ располагается в плоскости $χ$ и не равна точке $Н_{2}$ , тогда получаем прямоугольный треугольник вида $М_{2} H_{1} H_{2}$ , который является прямоугольным, где имеется катет $М_{2} H_{1}, М_{2} H_{2}$ – гипотенуза. Значит, отсюда следует, что $|M_{1} H_{1}| < |M_{1} H_{2}|$ . Тогда отрезок $М_{2} H_{1}$ считается наклонной, которая проводится из точки $М_{1}$ до плоскости $χ$ . Мы имеем, что перпендикуляр, проведенный из заданной точки к плоскости, меньше наклонной, которую проводят из точки к заданной плоскости. Рассмотрим этот случай на рисунке, приведенном ниже.

Расстояние от точки до плоскости – определение

Расстояние от точки до плоскости – теория, примеры, решения

Существует ряд геометрических задач, решения которых должны содержать расстояние от точки до плоскости. Способы выявления этого могут быть разными. Для разрешения применяют теорему Пифагора или подобия треугольников. Когда по условию необходимо рассчитать расстояние от точки до плоскости, заданные в прямоугольной системе координат трехмерного пространства, решают методом координат. Данный пункт рассматривает этот метод.

По условию задачи имеем, что задана точка трехмерного пространства с координатами $M_{1} (x_{1}, y_{1}, z_{1})$ с плоскостью $χ$ , необходимо определить расстояние от $М_{1}$ к плоскости $χ$ . Для решения применяется несколько способов решения.

Первый способ

Данный способ основывается на нахождении расстояния от точки до плоскости при помощи координат точки $Н_{1}$ , которые являются основанием перпендикуляра из точки $М_{1}$ к плоскости $χ$ . Далее необходимо вычислить расстояние между $М_{1}$ и $Н_{1}$ .

Для решения задачи вторым способом применяют нормальное уравнение заданной плоскости.

Второй способ

По условию имеем, что $Н_{1}$ является основанием перпендикуляра, который опустили из точки $М_{1}$ на плоскость $χ$ . Тогда определяем координаты $(x_{2}, y_{2}, z_{2})$ точки $Н_{1}$ . Искомое расстояние от $М_{1}$ к плоскости $χ$ находится по формуле $|M_{1} H_{1}| = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2} + (z_{2} - z_{1})^{2}}$ , где $M_{1} (x_{1}, y_{1}, z_{1})$ и $H_{1} (x_{2}, y_{2}, z_{2})$ . Для решения необходимо узнать координаты точки $Н_{1}$ .

Имеем, что $Н_{1}$ является точкой пересечения плоскости $χ$ с прямой $a$ , которая проходит через точку $М_{1}$ , расположенную перпендикулярно плоскости $χ$ . Отсюда следует, что необходимо составление уравнения прямой, проходящей через заданную точку перпендикулярно к заданной плоскости. Именно тогда сможем определить координаты точки $Н_{1}$ . Необходимо произвести вычисление координат точки пересечения прямой и плоскости.

Алгоритм нахождения расстояния от точки с координатами $M_{1} (x_{1}, y_{1}, z_{1})$ к плоскости $χ$ :

Определение 3

составить уравнение прямой а, проходящей через точку $М_{1}$ и одновременно
перпендикулярной к плоскости $χ$ ;
найти и вычислить координаты $(x_{2}, y_{2}, z_{2})$ точки $Н_{1}$ , являющимися точками
пересечения прямой $a$ с плоскостью $χ$ ;
вычислить расстояние от $М_{1}$ до $χ$ , используя формулу $|M_{1} H_{1}| = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2} + {(z_{2} - z_{1})}^{2}}$ .

Третий способ

В заданной прямоугольной системе координат $О х у z$ имеется плоскость $χ$ , тогда получаем нормальное уравнение плоскости вида $\cos α \cdot x + \cos β \cdot y + \cos γ \cdot z - p = 0$ . Отсюда получаем, что расстояние $|M_{1} H_{1}|$ с точкой $M_{1} (x_{1}, y_{1}, z_{1})$ , проведенной на плоскость $χ$ , вычисляемое по формуле $|M_{1} H_{1}| = |\cos α \cdot x + \cos β \cdot y + \cos γ \cdot z - p|$ . Эта формула справедлива, так как это установлено благодаря теореме.

Теорема

Если задана точка $M_{1} (x_{1}, y_{1}, z_{1})$ в трехмерном пространстве, имеющая нормальное уравнение плоскости $χ$ вида $\cos α \cdot x + \cos β \cdot y + \cos γ \cdot z - p = 0$ , тогда вычисление расстояния от точки до плоскости $|M_{1} H_{1}|$ производится из формулы $|M_{1} H_{1}| = |\cos α \cdot x + \cos β \cdot y + \cos γ \cdot z - p|$ , так как $x = x_{1}, y = y_{1}, z = z_{1}$ .

Доказательство

Доказательство теоремы сводится к нахождению расстояния от точки до прямой. Отсюда получаем, что расстояние от $M_{1}$ до плоскости $χ$ - это и есть модуль разности числовой проекции радиус-вектора $M_{1}$ с расстоянием от начала координат к плоскости $χ$ . Тогда получаем выражение $|M_{1} H_{1}| = |n p_{\vec{n}} \vec{O M} - p|$ . Нормальный вектор плоскости $χ$ имеет вид $\vec{n} = (\cos α, \cos β, \cos γ)$ , а его длина равняется единице, $n p_{\vec{n}} \vec{O M}$ - числовая проекция вектора $\vec{O M} = (x_{1}, y_{1}, z_{1})$ по направлению, определяемым вектором $\vec{n}$ .

Применим формулу вычисления скалярных векторов. Тогда получаем выражение для нахождения вектора вида $(\vec{n}, \vec{O M}) = |\vec{n}| \cdot n p_{\vec{n}} \vec{O M} = 1 \cdot n p_{\vec{n}} \vec{O M} = n p_{\vec{n}} \vec{O M}$ , так как $\vec{n} = (\cos α, \cos β, \cos γ \cdot z)$ и $\vec{O M} = (x_{1}, y_{1}, z_{1})$ . Координатная форма записи примет вид $(\vec{n}, \vec{O M}) = \cos α \cdot x_{1} + \cos β \cdot y_{1} + \cos γ \cdot z_{1}$ , тогда $|M_{1} H_{1}| = |n p_{\vec{n}} \vec{O M} - p| = |\cos α \cdot x_{1} + \cos β \cdot y_{1} + \cos γ \cdot z_{1} - p|$ . Теорема доказана.

Отсюда получаем, что расстояние от точки $M_{1} (x_{1}, y_{1}, z_{1})$ к плоскости $χ$ вычисляется при помощи подстановки в левую часть нормального уравнения плоскости $\cos α \cdot x + \cos β \cdot y + \cos γ \cdot z - p = 0$ вместо $х, у, z$ координаты $x_{1}, y_{1}$ и $z_{1}$ ,относящиеся к точке $М_{1}$ , взяв абсолютную величину полученного значения.

Рассмотрим примеры нахождения расстояния от точки с координатами до заданной плоскости.

Пример 1

Вычислить расстояние от точки с координатами $M_{1} (5, - 3, 10)$ к плоскости $2 x - y + 5 z - 3 = 0$ .

Решение

Решим задачу двумя способами.

Первый способ начнется с вычисления направляющего вектора прямой $a$ . По условию имеем, что заданное уравнение $2 x - y + 5 z - 3 = 0$ является уравнением плоскости общего вида, а $\vec{n} = (2, - 1, 5)$ является нормальным вектором заданной плоскости. Его применяют в качестве направляющего вектора прямой $a$ , которая перпендикулярна относительно заданной плоскости. Следует записать каноническое уравнение прямой в пространстве, проходящее через $M_{1} (5, - 3, 10)$ с направляющим вектором с координатами $(2, - 1, 5)$ .

Уравнение получит вид $\frac{x - 5}{2} = \frac{y - (- 3)}{- 1} = \frac{z - 10}{5} \Leftrightarrow \frac{x - 5}{2} = \frac{y + 3}{- 1} = \frac{z - 10}{5}$ .

Следует определить точки пересечения. Для этого нежно объединить уравнения в систему для перехода от канонического к уравнениям двух пересекающихся прямых. Данную точку примем за $Н_{1}$ . Получим, что

$\frac{x - 5}{2} = \frac{y + 3}{- 1} = \frac{z - 10}{5} \Leftrightarrow \{\begin{cases} \begin{array}{l} - 1 \cdot (x - 5) = 2 \cdot (y + 3) \\ 5 \cdot (x - 5) = 2 \cdot (z - 10) \end{array} \\ 5 \cdot (y + 3) = - 1 \cdot (z - 10) \end{cases} \Leftrightarrow \Leftrightarrow \{\begin{cases} \begin{array}{l} x + 2 y + 1 = 0 \\ 5 x - 2 z - 5 = 0 \end{array} \\ 5 y + z + 5 = 0 \end{cases} \Leftrightarrow \{\begin{cases} x + 2 y + 1 = 0 \\ 5 x - 2 z - 5 = 0 \end{cases}$

После чего необходимо разрешить систему

$\{\begin{cases} \begin{array}{l} x + 2 y + 1 = 0 \\ 5 x - 2 z - 5 = 0 \end{array} \\ 2 x - y + 5 z - 3 = 0 \end{cases} \Leftrightarrow \{\begin{cases} \begin{array}{l} x + 2 y = 1 \\ 5 x - 2 z = 5 \end{array} \\ 2 x - y + 5 z = 3 \end{cases}$

Обратимся к правилу решения системы по Гауссу:

$(\begin{matrix} 1 & 2 & 0 & - 1 \\ 5 & 0 & - 2 & 5 \\ 2 & - 1 & 5 & 3 \end{matrix}) ~ (\begin{matrix} 1 & 2 & 0 & - 1 \\ 0 & - 10 & - 2 & 10 \\ 0 & - 5 & 5 & 5 \end{matrix}) ~ (\begin{matrix} 1 & 2 & 0 & - 1 \\ 0 & - 10 & - 2 & 10 \\ 0 & 0 & 6 & 0 \end{matrix}) \Rightarrow \Rightarrow z = \frac{0}{6} = 0, y = - \frac{1}{10} \cdot (10 + 2 \cdot z) = - 1, x = - 1 - 2 \cdot y = 1$

Получаем, что $H_{1} (1, - 1, 0)$ .

Производим вычисления расстояния от заданной точки до плоскости. Берем точки $M_{1} (5, - 3, 10)$ и $H_{1} (1, - 1, 0)$ и получаем

$|M_{1} H_{1}| = \sqrt{(1 - 5)^{2} + (- 1 - (- 3))^{2} + (0 - 10)^{2}} = 2 \sqrt{30}$

Второй способ решения заключается в том, чтобы для начала привести заданное уравнение $2 x - y + 5 z - 3 = 0$ к нормальному виду. Определяем нормирующий множитель и получаем $\frac{1}{\sqrt{2^{2} + (- 1)^{2} + 5^{2}}} = \frac{1}{\sqrt{30}}$ . Отсюда выводим уравнение плоскости $\frac{2}{\sqrt{30}} \cdot x - \frac{1}{\sqrt{30}} \cdot y + \frac{5}{\sqrt{30}} \cdot z - \frac{3}{\sqrt{30}} = 0$ . Вычисление левой части уравнения производится посредствам подстановки $x = 5, y = - 3, z = 10$ , причем нужно взять расстояние от $M_{1} (5, - 3, 10)$ до $2 x - y + 5 z - 3 = 0$ по модулю. Получаем выражение:

$|M_{1} H_{1}| = |\frac{2}{\sqrt{30}} \cdot 5 - \frac{1}{\sqrt{30}} \cdot (- 3) + \frac{5}{\sqrt{30}} \cdot 10 - \frac{3}{\sqrt{30}}| = |\frac{60}{\sqrt{30}}| = 2 \sqrt{30}$

Ответ: $2 \sqrt{30}$ .

Когда плоскость $χ$ задается одним из способов раздела способы задания плоскости, тогда нужно для начала получить уравнение плоскости $χ$ и вычислять искомое расстояние при помощи любого метода.

Пример 2

В трехмерном пространстве задаются точки с координатами $M_{1} (5, - 3, 10), A (0, 2, 1), B (2, 6, 1), C (4, 0, - 1)$ . Вычислить расстяние от $М_{1}$ к плоскости $А В С$ .

Решение

Для начала необходимо записать уравнение плоскости, проходящее через заданные три точки с координатами $M_{1} (5, - 3, 10), A (0, 2, 1), B (2, 6, 1), C (4, 0, - 1)$ .

Получим:

$|\begin{matrix} x - 0 & y - 2 & z - 1 \\ 2 - 0 & 6 - 2 & 1 - 1 \\ 4 - 0 & 0 - 2 & - 1 - 1 \end{matrix}| = 0 \Leftrightarrow |\begin{matrix} x & y - 2 & z - 1 \\ 2 & 4 & 0 \\ 4 & - 2 & - 2 \end{matrix}| = 0 \Leftrightarrow \Leftrightarrow - 8 x + 4 y - 20 z + 12 = 0 \Leftrightarrow 2 x - y + 5 z - 3 = 0$

Отсюда следует, что задача имеет аналогичное предыдущему решение. Значит, расстояние от точки $М_{1}$ к плоскости $А В С$ имеет значение $2 \sqrt{30}$ .

Ответ: $2 \sqrt{30}$ .

Нахождение расстояния от заданной точки на плоскости или к плоскости, которым они параллельны, удобнее, применив формулу $|M_{1} H_{1}| = |\cos α \cdot x_{1} + \cos β \cdot y_{1} + \cos γ \cdot z_{1} - p|$ . Отсюда получим, что нормальные уравнения плоскостей получают в несколько действий.

Пример 3

Найти расстояние от заданной точки с координатами $M_{1} (- 3, \sqrt{2}, - 7)$ к координатной плоскости $О х у z$ и плоскости, заданной уравнением $2 y - 5 = 0$ .

Решение

Координатная плоскость $О у z$ соответствует уравнению вида $х = 0$ . Для плоскости $О у z$ оно является нормальным. Поэтому необходимо подставить в левую часть выражения значения $х = - 3$ и взять модуль значения расстояния от точки с координатами $M_{1} (- 3, \sqrt{2}, - 7)$ к плоскости. Получаем значение, равное $|- 3| = 3$ .

После преобразования нормальное уравнение плоскости $2 y - 5 = 0$ получит вид $y - \frac{5}{2} = 0$ . Тогда можно найти искомое расстояние от точки с координатами $M_{1} (- 3, \sqrt{2}, - 7)$ к плоскости $2 y - 5 = 0$ . Подставив и вычислив, получаем $|\sqrt{2} - \frac{5}{2}| = \frac{5}{2} - \sqrt{2}$ .

Ответ: Искомое расстояние от $M_{1} (- 3, \sqrt{2}, - 7)$ до $О у z$ имеет значение $3$ , а до $2 y - 5 = 0$ имеет значение $\frac{5}{2} - \sqrt{2}$ .

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.