- 16 июля 2025
- 9 минут
- 9 210
Угол между прямой и плоскостью: определение, примеры нахождения
Статью подготовили специалисты образовательного сервиса Zaochnik.
Статья начинается с определение угла между прямой и плоскостью. В данной статье будет показано нахождение угла между прямой и плоскостью методом координат. Подробно будут рассмотрены решение примеров и задач.
Угол между прямой и плоскостью – определение
Предварительно необходимо повторить понятие о прямой линии в пространстве и понятие плоскости. Для определения угла между прямой и плоскостью необходимый несколько вспомогательных определений. Рассмотрим эти определения подробно.
Прямая и плоскость пересекаются в том случае, когда они имеют одну общую точку, то есть она является точкой пересечения прямой и плоскости.
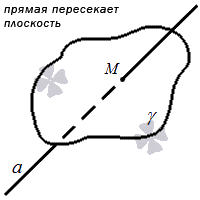
Прямая, пересекающая плоскость, может являться перпендикулярной относительно плоскости.
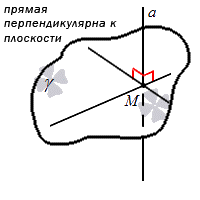
Прямая является перпендикулярной к плоскости, когда она перпендикулярна любой прямой, находящейся в этой плоскости.
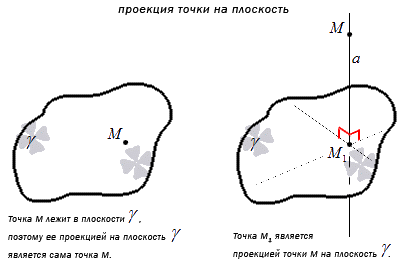
Проекция точки на плоскость является сама точка, если она лежит в заданной плоскости, либо является точкой пересечения плоскости с прямой, перпендикулярной плоскости , проходящей через точку , при условии, что она не принадлежит плоскости .
Проекция прямой а на плоскость - это множество проекций всех точек заданной прямой на плоскость.
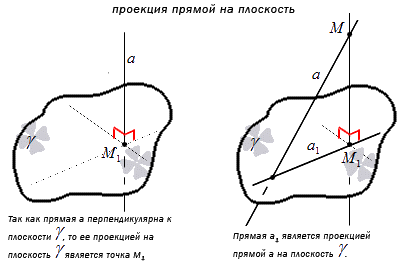
Отсюда получаем, что перпендикулярная к плоскости проекция прямой имеет точку пересечения. Получаем, что проекция прямой – это прямая, принадлежащая плоскости и проходящая через точку пересечения прямой и плоскости. Рассмотрим на рисунке, приведенном ниже.
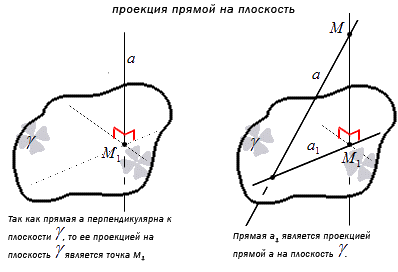
На данный момент имеем все необходимые сведения и данные для формулировки определения угла между прямой и плоскостью
Углом между прямой и плоскостью называют угол между этой прямой и ее проекцией на эту плоскость, причем прямая не перпендикулярна к ней.
Определение угла, приведенное выше, помогает прийти к выводу о том, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми, то есть заданной прямой вместе с ее проекцией на плоскость. Значит, угол между ними всегда будет острым. Рассмотрим на картинке, приведенной ниже.
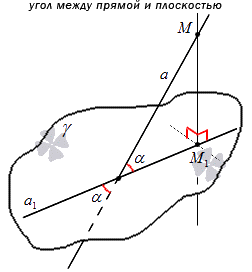
Угол, расположенный между прямой и плоскостью, считается прямым, то есть равным градусов, а угол, расположенный между параллельными прямыми, не определяется. Бывают случаи, когда его значение берется равным нулю.
Нахождение угла между прямой и плоскостью
Задачи, где необходимо найти угол между прямой и плоскостью, имеет множество вариация решения. Ход самого решения зависит от имеющихся данных по условию. Частыми спутниками решения являются признаки подобия или равенства фигур, косинусы, синусы, тангенсы углов. Нахождение угла возможно при помощи метода координат. Рассмотрим его более детально.
Если в трехмерном пространстве вводится прямоугольная система координат , тогда в ней задается прямая , пересекающая плоскость в точке , причем она не перпендикулярна плоскости. Необходимо найти угол , находящийся между заданной прямой и плоскостью.
Для начала необходимо применить определение угла между прямой и плоскостью методом координат. Тогда получим следующее.
В системе координат задается прямая , которой соответствуют уравнения прямой в пространстве и направляющий вектор прямой пространства, для плоскости соответствует уравнение плоскости и нормальный вектор плоскости. Тогда является направляющим вектором заданной прямой , а - нормальным вектором для плоскости . Если представить, что у нас имеются координаты направляющего вектора прямой и нормального вектора плоскости , тогда известны их уравнения, то есть заданы по условию, тогда есть возможность определения векторов и , исходя из уравнения.
Для вычисления угла необходимо преобразовать формулу, позволяющую получить значение этого угла при помощи имеющихся координат направляющего вектора прямой и нормального вектора.
Необходимо отложить векторы и , начиная от точки пересечения прямой с плоскостью . Существуют варианта расположения этих векторов относительно заданных прямых и плоскости. Рассмотри рисунок, приведенный ниже, на котором имеются все вариации.
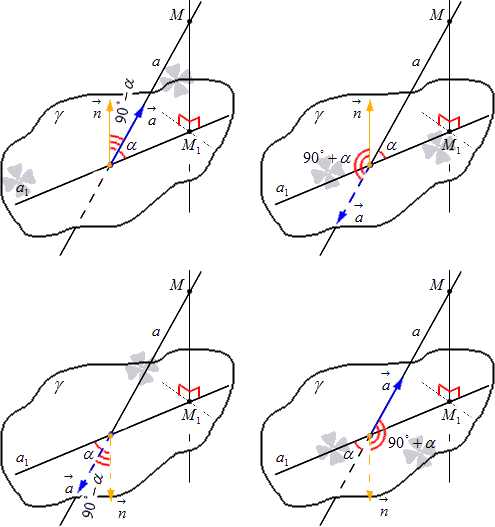
Отсюда получаем, что угол между векторами и имеет обозначение и является острым, тогда искомый угол , располагающийся между прямой и плоскостью, дополняется, то есть получаем выражение вида . Когда по условию , тогда имеем .
Отсюда имеем, что косинусы равных углов являются равными, тогда последние равенства записываются в виде системы
Необходимо использовать формулы приведения для упрощения выражений. Тогда получим равенства вида .
Проведя преобразования, система приобретает вид
Отсюда получим, что синус угла между прямой и плоскостью равен модулю косинуса угла между направляющим вектором прямой и нормальным вектором заданной плоскости.
Раздел нахождения угла, образованного двумя векторами, выявили, что этот угол принимает значение скалярного произведения векторов и произведения этих длин. Процесс вычисления синуса угла, полученного пересечением прямой и плоскости, выполняется по формуле
Значит, формулой для вычисления угла между прямой и плоскостью с координатами направляющего вектора прямой и нормального вектора плоскости после преобразования получается вида
Нахождение косинуса при известном синусе позволительно, применив основное тригонометрическое тождество. Пересечение прямой и плоскости образует острый угол. Это говорит о том, что его значение будет являться положительным числом, а его вычисление производится из формулы .
Выполним решение нескольких подобных примеров для закрепления материала.
Найти угол, синус, косинус угла, образованного прямой и плоскостью .
Решение
Для получения координат направляющего вектора необходимо рассмотреть канонические уравнения прямой в пространстве. Тогда получим, что является направляющим вектором прямой .
Для нахождения координат нормального вектора необходимо рассмотреть общее уравнение плоскости, так как их наличие определяется коэффициентами, имеющимися перед переменными уравнения. Тогда получим, что для плоскости нормальный вектор имеет вид .
Необходимо перейти к вычислению синуса угла между прямой и плоскостью. Для этого необходимо произвести подстановку координат векторов и в заданную формулу. Получаем выражение вида
Отсюда найдем значение косинуса и значение самого угла. Получим:
Ответ: .
Имеется пирамида, построенная при помощи значений векторов . Найти угол между прямой и плоскостью .
Решение
Для вычисления искомого угла, необходимо иметь значения координат направляющего вектора прямой и нормального вектора плоскости. для прямой направляющий вектор имеет координаты .
Нормальный вектор , принадлежащий плоскости , является перпендикулярным вектору и . Это подразумевает то, что нормальным вектором плоскости можно считать векторное произведение векторов и . Вычислим это по формуле и получим:
Необходимо произвести подстановку координат векторов для вычисления искомого угла, образованного пересечением прямой и плоскости. получим выражение вида:
Ответ: .
Математические онлайн-калькуляторы




