- 16 июля 2025
- 9 минут
- 61 323
Уравнение прямой, которая проходит через две заданные точки: примеры, решения
Статью подготовили специалисты образовательного сервиса Zaochnik.
Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.
Уравнение прямой, проходящей через две заданные точки на плоскости
Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.
Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.
Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой , проходящей через две несовпадающие точки и , находящиеся в декартовой системе координат.
В каноническом уравнении прямой на плоскости, имеющего вид , задается прямоугольная система координат с прямой, которая пересекается с ней в точке с координатами с направляющим вектором .
Необходимо составить каноническое уравнение прямой , которая пройдет через две точки с координатами и .
Прямая а имеет направляющий вектор с координатами, так как пересекает точки и . Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение с координатами направляющего вектора и координатами лежащих на них точках и . Получим уравнение вида или .
Рассмотрим рисунок, приведенный ниже.
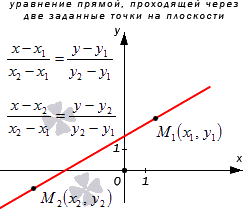
Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами и . Получим уравнение вида или .
Рассмотрим подробней на решении нескольких примеров.
Записать уравнение прямой, проходящей через заданные точки с координатами .
Решение
Каноническим уравнением для прямой, пересекающейся в двух точках с координатами и принимает вид . По условию задачи имеем, что . Необходимо подставить числовые значения в уравнение . Отсюда получим, что каноническое уравнение примет вид .
Ответ: .
При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.
Составить общее уравнение прямой, проходящей через точки с координатами и в системе координат .
Решение
Для начала необходимо записать каноническое уравнение заданной прямой, которая проходит через заданные две точки. Получим уравнение вида .
Приведем каноническое уравнение к искомому виду, тогда получим:
Ответ: .
Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид . Если необходимо найти значение углового коэффициента и числа , при которых уравнение определяет линию в системе которая проходит через точки и , где . Когда , тогда угловой коэффициент принимает значение бесконечности, а прямая определена общим неполным уравнением вида .
Потому как точки и находятся на прямой, тогда их координаты удовлетворяют уравнению и . Следует решить систему уравнений относительно и .
Для этого найдем или .
С такими значениями и уравнение прямой, проходящее через заданные две точки, принимает следующий вид или .
Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.
Записать уравнение прямой с угловым коэффициентом, проходящей через точки с координатами и .
Решение
Для решения задачи применяем формулу с угловым коэффициентом, имеющую вид . Коэффициенты и должны принимать такое значение, чтобы данное уравнение соответствовало прямой, проходящей через две точки с координатами и .
Точки и располагаются на прямой, тогда их координаты должны обращать уравнение верное равенство. Отсюда получаем, что и . Объединим уравнение в систему и решим.
При подстановке получаем, что
Теперь значения и подвергаются подстановке в уравнение . Получаем, что искомым уравнением, проходящим через заданные точки, будет уравнение, имеющее вид .
Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.
Запишем каноническое уравнение прямой, проходящей через и , имеющее вид .
Теперь переходим к уравнению в угловым коэффициентом. Получаем, что: .
Ответ: .
Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве
Если в трехмерном пространстве имеется прямоугольная система координат с двумя заданными несовпадающими точками с координатами и , проходящая через них прямая , необходимо получить уравнение этой прямой.
Имеем, что канонические уравнения вида и параметрические вида способны задать линию в системе координат , проходящую через точки, имеющие координаты с направляющим вектором .
Прямая имеет направляющий вектор вида , где прямая проходит через точку и , отсюда каноническое уравнение может быть вида или , в свою очередь параметрические или .
Рассмотрим рисунок, на котором изображены заданные точки в пространстве и уравнение прямой.
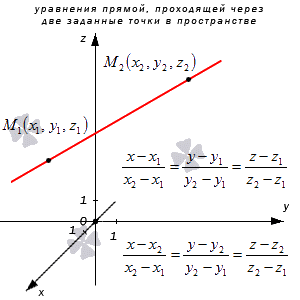
Написать уравнение прямой, определенной в прямоугольной системе координат трехмерного пространства, проходящей через заданные две точки с координатами и .
Решение
Необходимо найти каноническое уравнение. Так как речь идет о трехмерном пространстве, значит при прохождении прямой через заданные точки, искомое каноническое уравнение примет вид .
По условию имеем, что . Отсюда следует, что необходимые уравнения запишутся таким образом:
Ответ: .
Математические онлайн-калькуляторы




