Уравнения прямой, виды уравнений прямой в пространстве

Содержание:

24 ноября 2023
7 минут
2893

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Материал этой статьи продолжает тему прямой в пространстве. От геометрического описания пойдем к алгебраическому: зададим прямую при помощи уравнений в фиксированной прямоугольной системе координат трехмерного пространства. Приведем общую информацию, расскажем о видах уравнений прямой в пространстве и их связи между собой.

Уравнение прямой в пространстве: общие сведения

Определение 1

Уравнение прямой на плоскости в прямоугольной системе координат $O x y$ – это линейное уравнение с переменными $x$ и $y$ , которому отвечают координаты всех точек прямой и не удовлетворяют координаты никаких прочих точек.

Если речь идет о прямой в трехмерном пространстве, все несколько иначе: не существует такого линейного уравнения с тремя переменными $x, y, z$ , которому бы отвечали только координаты точек заданной прямой. В самом деле, уравнение $A x + B y + C z + D = 0$ , где $x, y, z$ – переменные, а $А, В, С$ и $D$ – некоторые действительные числа ( $А, В, С$ одновременно не равны нулю) – это общее уравнение плоскости. Тогда как же задать прямую линию в прямоугольной системе координат $O x y z$ ? Найдем ответ на этот вопрос в следующих пунктах темы.

Уравнение прямой в пространстве как уравнение двух пересекающихся плоскостей

Вспомним аксиому:

Определение 2

Когда две плоскости в пространстве имеют общую точку, существует их общая прямая, на которой находятся все общие точки этих плоскостей.

Рассмотрим это утверждение в алгебраическом толковании.

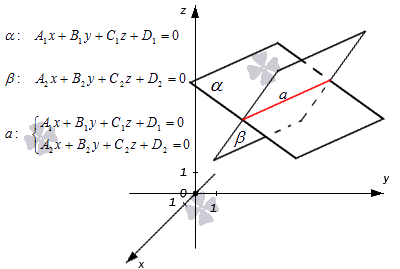
Допустим, в трехмерном пространстве зафиксирована прямоугольная система координат $O x y z$ и задано, что прямая $a$ – это линия пересечения двух плоскостей $α$ и $β$ , которые соответственно описываются уравнениями плоскости $A_{1} x + B_{1} y + C_{1} z + D_{1} = 0$ и $A_{2} x + B_{2} y + C_{2} z + D_{2} = 0$ . Поскольку прямая $a$ – это множество общих точек плоскостей $α$ и $β$ , то координаты любой точки прямой $a$ будут одновременно отвечать обоим уравнениям. Никакие прочие точки одновременно удовлетворять условия обоих уравнений не будут.

Таким образом, координаты любой точки прямой $a$ в прямоугольной системе координат станут частным решением системы линейных уравнений вида

$\{\begin{cases} A_{1} x + B_{1} y + C_{1} z + D_{1} = 0 \\ A_{2} x + B_{2} y + C_{2} z + D_{2} = 0 \end{cases}$

Общее же решение системы уравнений _ $\{\begin{cases} A_{1} x + B_{1} y + C_{1} z + D_{1} = 0 \\ A_{2} x + B_{2} y + C_{2} z + D_{2} = 0 \end{cases}$ определит координаты каждой точки прямой $a$ , т.е. по сути задает саму прямую $a$ .

Уравнение прямой в пространстве как уравнение двух пересекающихся плоскостей

Резюмируем: прямая в пространстве в прямоугольной системе координат $O x y z$ может быть задана системой уравнений двух плоскостей, которые пересекаются:

$\{\begin{cases} A_{1} x + B_{1} y + C_{1} z + D_{1} = 0 \\ A_{2} x + B_{2} y + C_{2} z + D_{2} = 0 \end{cases}$

Приведем пример описания прямой линии в пространстве при помощи системы уравнений:

$\{\begin{cases} x + 3 y - 2_{1} z + 11 \\ 3 y + \frac{1}{4} z - \sqrt{2} = 0 \end{cases}$

Навык определения прямой линии уравнениями пересекающихся плоскостей необходим при решении задач на нахождение координат точки пересечения прямой и плоскости или нахождение координат точки пересечения двух прямых в пространстве.

Подробнее изучить эту тему можно, обратившись к статье об уравнениях прямой в пространстве, уравнениях двух пересекающихся прямых.

Заметим, что существует несколько способов описания прямой в пространстве. В практике прямую чаще задают не двумя пересекающимися плоскостями, а направляющим вектором прямой и точкой, принадлежащей этой прямой. В подобных случаях легче задать канонические и параметрические уравнения прямой в пространстве. Поговорим о них ниже.

Параметрические уравнения прямой в пространстве

$\{\begin{cases} \begin{array}{l} x = x_{1} + a_{x} \cdot λ \\ y = y_{1} + a_{y} \cdot λ \end{array} \\ z = z_{1} + a_{z} \cdot λ \end{cases}$ , где $x_{1}, y_{1}, z_{1}$ – координаты некой точки прямой; $а_{x}, а_{y}$ и $a_{z}$ (одновременно не равны нулю) – координаты направляющего вектора прямой. $а \cdot λ$ – некий параметр, принимающий любые действительные значения.

Любое значение параметра $λ$ позволяет, используя параметрические уравнения прямой в пространстве, определить тройку чисел $(x, y, z)$ , соответствующую некой точке прямой (отсюда и название такого вида уравнений). Например, пусть $λ = 0$ , тогда из параметрических уравнений прямой в пространстве получим координаты:

$\{\begin{cases} \begin{array}{l} x = x_{1} + a_{x} \cdot 0 \\ y = y_{1} + a_{y} \cdot 0 \end{array} \\ z = z_{1} + a_{z} \cdot 0 \end{cases} \Leftrightarrow \{\begin{cases} \begin{array}{l} x = x_{1} \\ y = y_{1} \end{array} \\ z = z_{1} \end{cases}$

Рассмотрим конкретный пример:

Пример 1

Пусть прямая задана параметрическими уравнениями вида $\{\begin{cases} \begin{array}{l} x = 3 + 2 \cdot a_{x} \\ y = - 2 \cdot a_{y} \end{array} \\ z = 2 + \sqrt{2} \cdot a_{z} \end{cases}$ .

Заданная прямая проходит через точку $М_{1} (3, 0, 2)$ ; направляющий вектор этой прямой имеет координаты $(2, - 2, \sqrt{2})$ .

Ответ: $(2, - 2, \sqrt{2})$ ,

Продолжение изучения этой темы можно найти в статье о параметрических уравнениях прямой в пространстве.

Канонические уравнения прямой в пространстве

Если разрешить каждое из параметрических уравнений прямой

$\{\begin{cases} \begin{array}{l} x = x_{1} + a_{x} \cdot λ \\ y = y_{1} + a_{y} \cdot λ \end{array} \\ z = z_{1} + a_{z} \cdot λ \end{cases}$ относительно параметра $λ$ , возможно просто перейти к каноническим уравнениям прямой в пространстве $\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}}$ .

Канонические уравнения прямой в пространстве задают прямую, которая проходит через точку $М_{1} (x_{1}, y_{1}, z_{1})$ , и у которой направляющий вектор равен $\vec{a} = (a_{x}, a_{y}, a_{z})$ . Например, задана прямая, описываемая каноническим уравнением $\frac{x - 1}{1} = \frac{y}{2} = \frac{z + \sqrt{5}}{7}$ . Эта прямая проходит через точку с координатами $(1, 0, - \sqrt{5})$ , ее направляющий вектор имеет координаты $(1, 2, - 7)$ .

Отметим, что одно или два числа из чисел $а_{x}, а_{y}$ и $а_{z}$ в канонических уравнениях прямой могут быть равны нулю (все три числа не могут быть равны нулю, поскольку направляющий вектор не может быть нулевым). В таком случае запись вида $\frac{x - x_{1}}{a_{x}} = \frac{y - y_{1}}{a_{y}} = \frac{z - z_{1}}{a_{z}}$ является формальной (поскольку в знаменателях одной или двух дробей будут нули) и понимать ее нужно как:

$\{\begin{cases} \begin{array}{l} x = x_{1} + a_{x} \cdot λ \\ y = y_{1} + a_{y} \cdot λ \end{array} \\ z = z_{1} + a_{z} \cdot λ \end{cases}$ , где $λ \in R$ .

Если одно из чисел $а_{x}, а_{y}$ и $a_{z}$ канонического уравнения прямой равно нулю, то прямая лежит в какой-то из координатных плоскостей, или в плоскости, ей параллельной. Если два из чисел $а_{x}, а_{y}$ и $a_{z}$ равны нулю, то прямая или совпадает с какой-либо из координатных осей, или параллельна ей. К примеру, прямая, описываемая каноническим уравнением $\frac{x + 4}{3} = \frac{y - 5}{2} = \frac{z + 2}{0}$ , лежит в плоскости $z = - 2$ , параллельной координатной плоскости $O x y$ , а координатная ось $O y$ описывается каноническими уравнениями $\frac{x}{0} = \frac{y}{1} = \frac{z}{0}$ .

Графические иллюстрации подобных случаев, составление канонических уравнений прямой в пространстве, примеры решения типовых задач, а также алгоритм перехода от канонических уравнений к другим видам уравнений прямой в пространстве рассмотрены в статье о канонических уравнениях прямой в пространстве.