- 21 июля 2025
- 24 минуты
- 13 197
Нахождение пересечения и объединения числовых множеств, что такое пересечение множеств
Статью подготовили специалисты образовательного сервиса Zaochnik.
Решение некоторых математических задач предполагает нахождение пересечения и объединения числовых множеств. В статье ниже рассмотрим эти действия подробно, в том числе, на конкретных примерах. Полученный навык будет применим для решения неравенств с одной переменной и систем неравенств.
Простейшие случаи
Когда мы говорим о простейших случаях в рассматриваемой теме, то имеем в виду нахождение пересечения и объединения числовых множеств, представляющих из себя набор отдельных чисел. В подобных случаях будет достаточно использования определения пересечения и объединения множеств.
Объединение двух множеств – это множество, в котором каждый элемент является элементом одного из исходных множеств.
Пересечение множеств – это множество, которое состоит из всех общих элементов исходных множеств.
Из указанных определений логически следуют следующие правила:
- чтобы составить объединение двух числовых множеств, имеющих конечное количество элементов, необходимо записать все элементы одного множества и дописать к ним недостающие элементы из второго множества;
- чтобы составить пересечение двух числовых множеств, необходимо элементы первого множества один за другим проверить на принадлежность второму множеству. Те из них, которые окажутся принадлежащими обоим множествам и будут составлять пересечение.
Полученное согласно первому правилу множество будет включать в себя все элементы, принадлежащие хотя бы одному из исходных множеств, т.е. станет объединением этих множеств по определению.
Множество, полученное согласно второму правилу, будет включать в себя все общие элементы исходных множеств, т.е. станет пересечением исходных множеств.
Рассмотрим применение полученных правил на практических примерах.
Исходные данные: числовые множества и . Необходимо найти объединение и пересечение исходных множеств.
Решение
- Определим объединение исходных множеств. Запишем все элементы, к примеру, множества . Добавим к ним недостающие элементы множества и . В конечном итоге имеем числовое множество:. Упорядочим элементы полученного множества и получим искомое объединение: .
- Определим пересечение исходных множеств. Согласно правилу, переберем один за другим все элементы первого множества и проверим, входят ли они во множество . Рассмотрим первый элемент - число : он не принадлежит множеству , а значит не будет являться элементом искомого пересечения. Проверим второй элемент множества , т.е. число : оно принадлежит множеству , а значит станет первым элементом искомого пересечения. Третий элемент множества – число . Оно не является элементом множества , а, следовательно, не является элементом пересечения. Рассмотрим последний элемент множества : число . Оно также принадлежит и множеству , и соответственно станет одним из элементов пересечения. Таким образом, пересечение исходных множеств – множество, состоящее из двух элементов: и , т.е. .
Ответ: объединение исходных множеств – ; пересечение исходных множеств - .
Все вышесказанное относится к работе с двумя множествами. Что же касается нахождения пересечения и объединения трех и более множеств, то решение этой задачи возможно свести к последовательному нахождению пересечения и объединения двух множеств. Например, чтобы определить пересечение трех множеств , и , возможно сначала определить пересечение и , а затем найти пересечение полученного результата с множеством . На примере это выглядит так: пусть будут заданы числовые множества: , и . Пересечение первых двух множеств составит: , а пересечение полученного множества с множеством . В итоге: .
Однако на практике, чтобы найти объединение и пересечение трех и более простейших числовых множеств, которые состоят из конечного количества отдельных чисел, удобнее применять правила, аналогичные указанным выше.
Т.е., чтобы найти объединение трех и более множеств указанного типа, необходимо к элементам первого множества добавить недостающие элементы второго множества, затем – третьего и т.д. Для пояснения возьмем числовые множества:. К элементам первого множества добавится число из множества , а затем – недостающие числа и множества . Таким образом, объединение исходных множеств: .
Что же касается решения задачи на нахождение пересечения трех и более числовых множеств, которые состоят из конечного количества отдельных чисел, необходимо одно за другим перебрать числа первого множества и поэтапно проверять, принадлежит ли рассматриваемое число каждому из оставшихся множеств. Для пояснения рассмотрим числовые множества:
Найдем пересечение исходных множеств. Очевидно, что множество имеет меньше всего элементов, поэтому именно их мы будем проверять, определяя, входят ли они в остальные множества. Число множества является элементом и прочих множеств, а значит является первым элементом искомого пересечения. Второе число множества – число – не является элементом множества , а, следовательно, не станет элементом пересечения. Продолжаем проверку: число множества является элементом прочих множеств и становится еще одной частью пересечения. Наконец, последний элемент множества – число – не является элементом множества и не является элементом пересечения. Таким образом, получаем:
Координатная прямая и числовые промежутки как объединение их частей
Отметим на координатной прямой произвольную точку, например, с координатой . Указанная точка разобьет координатную прямую на два числовых промежутка – два открытых луча (-∞, -5,4) и (-5,4, +∞) и собственно точку. Нетрудно увидеть, что в соответствии с определением объединения множеств любое действительное число будет принадлежать объединению . Т.е. множество всех действительных чисел возможно представить в виде полученного выше объединения. И наоборот, полученное объединение будет являться множеством всех действительных чисел.
Отметим, что заданную точку возможно присоединить к любому из открытых лучей, тогда он станет простым числовым лучом или . При этом множество R будет описываться следующими объединениями: или .
Подобные рассуждения действительны не только относительно точки координатной прямой, но и относительно точки на любом числовом промежутке. Т.е., если мы возьмем любую внутреннюю точку любого произвольного промежутка, его возможно будет представить, как объединение его частей, полученных после деления заданной точкой, и самой точки. К примеру, задан полуинтервал и точка , принадлежащая этому числовому промежутку. Тогда заданный полуинтервал можно представить в виде объединения и обратно. Мы можем включить число в любой из промежутков и тогда заданное множество можно представить, как или . Также мы можем взять в качестве исходных данных не внутреннюю точку заданного полуинтервала, а его конец (точку с координатой ), тогда заданный полуинтервал можно представить, как объединение интервала и множества из одного элемента . Таким образом: .
Еще один вариант: когда берется не одна, а несколько точек на координатной прямой или числовом промежутке. Эти точки разобьют координатную прямую или числовой промежуток на несколько числовых промежутков, а объединение этих промежутков будут составлять исходные множества. К примеру, на координатной прямой заданы точки с координатами , которые разобьют ее на промежутки: . При этом множество всех действительных чисел, олицетворением чего и является координатная прямая, возможно представить в виде объединения полученных промежутков и указанных чисел:
.
Как определить пересечение и объединение при помощи изображений числовых множеств
С темой нахождения пересечения и объединения множеств возможно наглядно разобраться, если использовать изображения заданных множеств на координатной прямой (если только речь – не о простейших случаях, рассмотренных в самом начале статьи).
Мы рассмотрим общий подход, который позволяет определить результат пересечения и объединения двух числовых множеств. Опишем подход в виде алгоритма. Рассматривать его шаги будем постепенно, каждый раз приводя очередной этап решения конкретного примера.
Исходные данные: заданы числовые множества и . Необходимо найти пересечение и объединение данных множеств.
Решение
- Изобразим заданные числовые множества на координатных прямых. Их необходимо расположить друг над другом. Для удобства принято считать, что точки начала отсчета заданных множеств совпадают, и остается сохранным расположение точек друг относительно друга: любая точка с большей координатой лежит правее точки с меньшей координатой. При этом, если нам интересно объединение множеств, то координатные прямые объединяют слева квадратной скобкой совокупности; если интересует пересечение, то – фигурной скобкой системы.
В нашем примере для записи пересечения и объединения числовых множеств имеем: 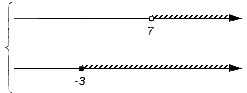 и
и 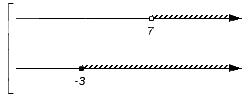
Изобразим еще одну координатную прямую, расположив ее под уже имеющимися. Она понадобится для отображения искомого пересечения или объединения. На этой координатной прямой отмечают все граничные точки исходных числовых множеств: сначала черточками, а позже, после выяснения характера точек с этими координатами, черточки будет заменены выколотыми или невыколотыми точками. В нашем примере это точки с координатами и .
Получим:
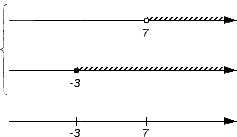 и
и 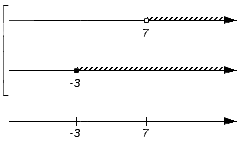
Точки, которые изображены на нижней координатной прямой в предыдущем шаге алгоритма, дают возможность рассматривать координатную прямую как набор числовых промежутков и точек (об этом мы говорили выше).
Ответ: В нашем примере координатную прямую представим в виде набора пяти числовых множеств: .
Теперь необходимо поочередно проверить принадлежность каждого из записанных множеств искомому пересечению или объединению. Получаемые выводы поэтапно отмечаются на нижней координатной прямой: когда промежуток является частью пересечения или объединения, над ним рисуется штриховка. Когда точка входит в пересечение или объединение, то штрих заменяется на сплошную точку; если точка не является частью пересечения или объединения – ее делают выколотой. В этих действиях нужно придерживаться таких правил:
-. промежуток становится частью пересечения, если он одновременно является частью множества и множества (или иными словами – если есть штриховка над этим промежутком на обеих координатных прямых, отображающих множества и );
- точка становится частью пересечения, если она является одновременно частью каждого из множеств и (иными словами – если точка является невыколотой или внутренней точкой какого-либо интервала обоих числовых множеств и );
- промежуток становится частью объединения, если он является частью хотя бы одного из множеств или (иными словами – если присутствует штриховка над этим промежутком хотя бы на одной из координатных прямых, отображающих множества и .
- точка становится частью объединения, если она является частью хотя бы одного из множеств и (иными словами – точка является невыколотой или внутренней точкой какого-либо интервала хотя бы одного из множеств и ).
Кратко резюмируя: пересечением числовых множеств и служит пересечение всех числовых промежутков множеств и , над которыми одновременно присутствует штриховка, и всех отдельных точек, принадлежащих и множеству А, и множеству В. Объединением числовых множеств и служит объединение всех числовых промежутков, над которыми присутствует штриховка хотя бы у одного из множеств или , а также всех невыколотых отдельных точек.
- Вернемся к примеру, определим пересечение заданных множеств. Для этого поочередно проверим множества: . Начнем с множества , наглядно выделив его на чертеже:
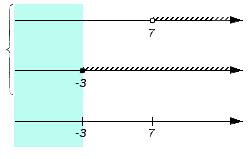
Этот промежуток не будет включен в пересечение, потому что не является частью ни множества , ни множества (нет штриховки). И так наш чертеж сохраняет свой изначальный вид:
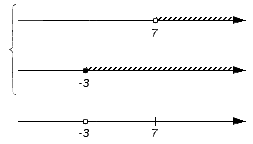
Рассмотрим следующее множество. Число является частью множества (невыколотой точкой), но не входит в состав множества , а потому не станет частью искомого пересечения. Соответственно на нижней координатной прямой точку с координатой делаем выколотой:
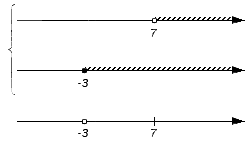
Оцениваем следующее множество .
Оно является частью множества (над интервалом присутствует штриховка), но не входит в множество (над интервалом штриховка отсутствует): не будет входить в искомое пересечение, а значит на нижней координатной прямой не появляется никаких новых отметок:
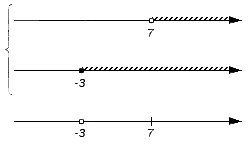
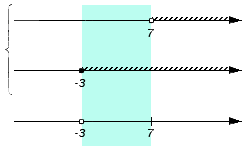
Следующее множество на проверку - . Оно является составом множества (точка с координатой является внутренней точкой промежутка ), но не является частью множества (выколотая точка), таким образом, рассматриваемый промежуток не станет частью искомого пересечения.. Отметим точку с координатой как выколотую:
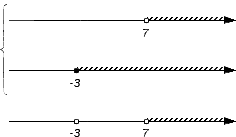
И, наконец, проверяем оставшийся промежуток .
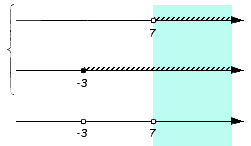
Промежуток входит в оба множества и (над промежутком присутствует штриховка), следовательно, становится частью пересечения. Штрихуем место над рассмотренным промежутком:
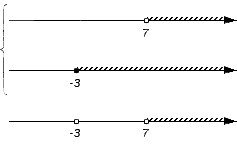
В конечном счете на нижней координатной прямой образовалось изображение искомого пересечения заданных множеств. Очевидно, что оно является множеством всех действительных чисел больше числа , т.е.: .
- Следующим шагом определим объединение заданных множеств и . Последовательно проверим множества , устанавливая факт включения или невключения их в искомое объединение.
Первое множество не является частью ни одного из исходных множеств и (над промежутками нет штриховок), следовательно, множество не войдет в искомое объединение:
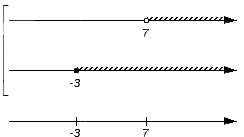
Множество входит в множество , а значит будет входить в искомое объединение множеств и :
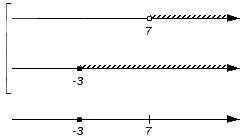
Множество является составной частью множества (над интервалом присутствует штриховка) и становится элементом объединения множеств и :
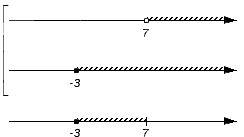
Множество входит в числовое множество , поэтому войдет и в искомое объединение:
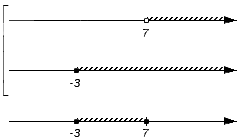
Множество , являясь элементом обоих множеств и одновременно, становится еще одной частью искомого объединения:
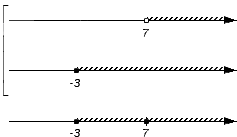
По итоговому изображению объединения исходных множеств и получаем: .
Имея некий практический опыт применения правил нахождения пересечений и объединений множеств, описанные проверки легко проводятся устно, что позволяет быстро записывать конечный результат. Продемонстрируем на практическом примере, как выглядит его решение без детальных пояснений.
Исходные данные: множества и . Необходимо определить пересечение и объединение заданных множеств.
Решение
Отметим заданные числовые множества на координатных прямых, чтобы иметь возможность получить иллюстрацию искомых пересечения и объединения:


Ответ: .
Также понятно, что при достаточном понимании процесса указанный алгоритм возможно подвергнуть оптимизации. К примеру, в процессе нахождения пересечения можно не тратить время на проверку всех промежутков и множеств, представляющих собой отдельные числа, ограничившись рассмотрением только тех промежутков и чисел, которые составляют множество А или В. Прочие промежутки в любом случае не войдут в пересечение, т.к. не являются частью исходных множеств. Составим иллюстрацию сказанного на практическом примере.
Исходные данные: множества и .
Необходимо определить пересечение исходных множеств.
Решение
Геометрически изобразим числовые множества и :
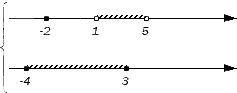
Граничные точки исходных множеств разобьют числовую прямую на несколько множеств:
.
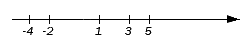
Легко заметить, что числовое множество можно записать, объединив некоторые из перечисленных множеств, а именно: , и . Достаточно будет проверить эти множества на их включенность также в множество В для того, чтобы найти искомое пересечение. Те, что войдут в множество В и станут элементами пересечения. Проведем проверку.
Совершенно понятно, что является частью множества , ведь точка с координатой – внутренняя точка отрезка . Интервал и множество также входят в множество (над интервалом присутствует штриховка, а точка с координатой является для множества В граничной и невыколотой). Множество не будет элементом пересечения, т.к. не входит в множество (над ним не присутствует штриховка). Отметим все вышесказанное на чертеже:
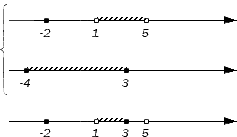
В итоге искомым пересечением двух заданных множеств будет объединение множеств, которое мы запишем так: .
Ответ: .
В заключении статьи обговорим еще, как решить задачу о нахождении пересечения и объединения нескольких множеств (более ). Сведем ее, как рекомендовалось ранее, к необходимости определения пересечения и объединения первых двух множеств, затем полученного результата с третьим множеством и так далее. А можно использовать описанный выше алгоритм с единственным только отличием, что проверку вхождения промежутков и множеств, представляющих собой отдельные числа, необходимо проводить не по двум, а всем заданным множествам. Рассмотрим на примере.
Исходные данные: множества . Необходимо определить пересечение и объединение заданных множеств.
Решение
Отображаем заданные числовые множества на координатных прямых и ставим с левой от них стороны фигурную скобку, обозначая пересечение, а также квадратную, обозначая объединение. Ниже отобразим координатные прямые с отмеченными штрихами граничными точками числовых множеств:
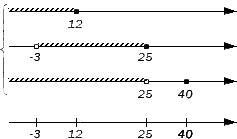
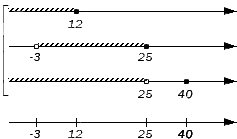
Таким образом, координатная прямая представлена следующими множествами: .
Начинаем искать пересечения, поочередно проверяя записанные множества на принадлежность каждому из исходных. Во все три заданных множества входит интервал и множество : они и станут элементами искомого пересечения. Таким образом, получим: .
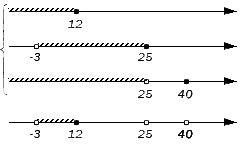
Объединение заданных множеств составят множества: - элемент множества – элемент множества – элемент множества – элемент множества – элемент множества – элемент множества и – элемент множества . Таким образом, получим: .
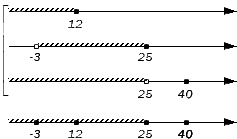
Ответ: .
Отметим также, что искомое пересечение числовых множеств часто является пустым множеством. Происходит это в тех случаях, когда в заданные множества не включены элементы, одновременно принадлежащие им всем.
Исходные данные: . Определить пересечение заданных множеств.
Решение
Отобразим исходные множества на координатных прямых и штрихами граничные точки этих множеств на дополнительной прямой.

Отмеченные точки разобьют числовую прямую на множества: .
Ни одно из них не является одновременно элементом всех исходных множеств, следовательно, пересечение заданных множеств есть пустое множество.
Ответ: .
Множества удобно изображать в виде кругов, которые называют кругами Эйлера.
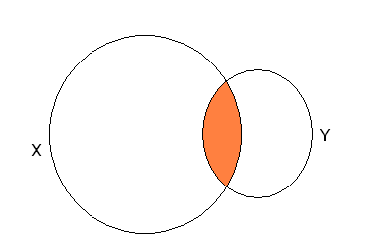
На рисунке множество пересечения множеств X и Y закрашено в оранжевый цвет.
Математические онлайн-калькуляторы




