- 16 июля 2025
- 16 минут
- 7 832
Степень числа: определения, обозначение, примеры
Статью подготовили специалисты образовательного сервиса Zaochnik.
В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.
Степени с натуральными показателями: понятие квадрата и куба числа
Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой ), а в качестве показателя – натуральное (обозначим буквой ).
Степень числа с натуральным показателем – это произведение -ного числа множителей, каждый из которых равен числу . Записывается степень так: , а в виде формулы ее состав можно представить следующим образом: 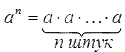
Например, если показатель степени равен , а основание – , то первая степень числа a записывается как . Учитывая, что – это значение множителя, а – число множителей, мы можем сделать вывод, что .
В целом можно сказать, что степень – это удобная форма записи большого количества равных множителей. Так, запись вида можно сократить до . Примерно так же произведение помогает нам избежать записи большого числа слагаемых ; мы это уже разбирали в статье, посвященной умножению натуральных чисел.
Как же верно прочесть запись степени? Общепринятый вариант – « в степени ». Или можно сказать «-ная степень» либо « -ной степени». Если, скажем, в примере встретилась запись , мы можем прочесть « в -й степени», « в степени » или «-я степень -ми».
Вторая и третья степени числа имеют свои устоявшиеся названия: квадрат и куб. Если мы видим вторую степень, например, числа , то мы можем сказать « в квадрате» или «квадрат числа ». Аналогично третья степень читается так: – это «куб числа» или « в кубе». Впрочем, употреблять стандартную формулировку «во второй/третьей степени» тоже можно, это не будет ошибкой.
Разберем пример степени с натуральным показателем: для пятерка будет основанием, а семерка – показателем.
В основании не обязательно должно стоять целое число: для степени основанием будет дробь , а показателем – девятка. Обратите внимание на скобки: такая запись делается для всех степеней, основания которых отличаются от натуральных чисел.
Например: .
Для чего нужны скобки? Они помогают избежать ошибок в расчетах. Скажем, у нас есть две записи: и . Первая из них означает отрицательное число минус два, возведенное в степень с натуральным показателем три; вторая – число, соответствующее противоположному значению степени .
Иногда в книгах можно встретить немного другое написание степени числа – (где а – основание, а - показатель). То есть – это то же самое, что и . В случае, если n представляет собой многозначное число, оно берется в скобки. Например, . Но мы будем использовать обозначение как более употребительное.
О том, как вычислить значение степени с натуральным показателем, легко догадаться из ее определения: нужно просто перемножить a -ное число раз. Подробнее об этом мы писали в другой статье.
Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.
Что такое степени с целым показателем
В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.
Степень числа с целым положительным показателем можно отобразить в виде формулы: 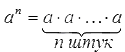 .
.
При этом – любое целое положительное число.
Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:
Равенство будет верно при условиях: и – натуральные числа, , .
Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения и равны, то мы получим следующий результат:
Но при этом - частное равных чисел и . Выходит, что нулевая степень любого отличного от нуля числа равна единице.
Однако такое доказательство не подходит для нуля в нулевой степени. Для этого нам нужно другое свойство степеней – свойство произведений степеней с равными основаниями. Оно выглядит так: .
Если n у нас равен , то (такое равенство также доказывает нам, что ). Но если а также равно нулю, наше равенство приобретает вид , Оно будет верным при любом натуральном значении и неважно при этом, чему именно равно значение степени , то есть оно может быть равно любому числу, и на верность равенства это не повлияет. Следовательно, запись вида своего особенного смысла не имеет, и мы не будем ему его приписывать.
При желании легко проверить, что сходится со свойством степени при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.
Разберем пример с конкретными числами: Так, - единица, , , а значение не определено.
После нулевой степени нам осталось разобраться, что из себя представляет степень отрицательная. Для этого нам понадобится то же свойство произведения степеней с равными основаниями, которое мы уже использовали выше: .
Введем условие: , тогда a не должно быть равно нулю. Из этого следует, что . Выходит, что и у нас являются взаимно обратными числами.
В итоге a в целой отрицательной степени есть не что иное, как дробь .
Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).
Степень a с целым отрицательным показателем n можно представить в виде дроби . Таким образом, при условии и – любое натуральное число.
Проиллюстрируем нашу мысль конкретными примерами:
В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:
Степень числа a с натуральным показателем – это:
Что такое степени с рациональным показателем
Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.
Что такое рациональные числа? В их множество входят как целые, так и дробные числа, при этом дробные числа можно представить в виде обыкновенных дробей (как положительных, так и отрицательных). Сформулируем определение степени числа с дробным показателем , где – натуральное число, а – целое.
У нас есть некоторая степень с дробным показателем . Для того, чтобы свойство степени в степени выполнялось, равенство должно быть верным.
Учитывая определение корня -ной степени и что , мы можем принять условие , если имеет смысл при данных значениях и .
Приведенные выше свойства степени с целым показателем будут верными при условии .
Основной вывод из наших рассуждений таков: степень некоторого числа с дробным показателем – это корень -ой степени из числа в степени . Это справедливо в том случае, если при данных значениях и выражение сохраняет смысл.
Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.
1. Мы можем ограничить значение основания степени: возьмем , которое при положительных значениях будет больше или равно , а для отрицательных – строго меньше (поскольку при мы получаем , а такая степень не определена). В таком случае определение степени с дробным показателем будет выглядеть следующим образом:
Степень с дробным показателем для некоторого положительного числа есть корень -ной степени из a, возведенного в степень . В виде формулы это можно изобразить так:
Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.
Степень с нулевым основанием и дробным положительным показателем можно выразить как
при условии целого положительного и натурального .
При отрицательном отношении степень не определяется, т.е. такая запись смысла не имеет.
Отметим один момент. Поскольку мы ввели условие, что больше или равно нулю, то у нас оказались отброшены некоторые случаи.
Выражение иногда все же имеет смысл при некоторых отрицательных значениях и некоторых . Так, верны записи , в которых основание отрицательно.
2. Второй подход – это рассмотреть отдельно корень с четными и нечетными показателями. Тогда нам потребуется ввести еще одно условие: степень , в показателе которой стоит сократимая обыкновенная дробь, считается степенью , в показателе которой стоит соответствующая ей несократимая дробь. Позже мы объясним, для чего нам это условие и почему оно так важно. Таким образом, если у нас есть запись , то мы можем свести ее к и упростить расчеты.
Если – нечетное число, а значение – положительно, – любое неотрицательное число, то имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.
Объединим все данные выше определения в одной записи:
Здесь m/n означает несократимую дробь, – любое целое число, а – любое натуральное число.
Для любой обыкновенной сократимой дроби степень можно заменить на .
Степень числа с несократимым дробным показателем – можно выразить в виде в следующих случаях: - для любых действительных , целых положительных значений и нечетных натуральных значений. Пример: .
- для любых отличных от нуля действительных , целых отрицательных значений и нечетных значений , например,
- для любых неотрицательных , целых положительных значений и четных , например, .
- для любых положительных , целых отрицательных и четных, например, .
В случае других значений степень с дробным показателем не определяется. Примеры таких степеней: .
Теперь объясним важность условия, о котором говорили выше: зачем заменять дробь с сократимым показателем на дробь с несократимым. Если бы мы этого не сделали бы, то получились бы такие ситуации, скажем, . Тогда должно быть верным , но , а .
Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.
Таким образом, степень положительного числа с дробным показателем определяется как . В случае отрицательных запись не имеет смысла. Степень нуля для положительных дробных показателей определяется как , для отрицательных дробных показателей мы степень нуля не определяем.
В выводах отметим, что можно записать любой дробный показатель как в виде смешанного числа, так и в виде десятичной дроби: .
При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:
Что такое степени с иррациональным и действительным показателем
Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.
Допустим, что у нас есть иррациональное число и последовательность его десятичных приближений . Например, возьмем значение тогда
и так далее (при этом сами приближения являются рациональными числами).
Последовательности приближений мы можем поставить в соответствие последовательность степеней . Если вспомнить, что мы рассказывали ранее о возведении чисел в рациональную степень, то мы можем сами подсчитать значения этих степеней.
Возьмем для примера , тогда и т.д.
Последовательность степеней можно свести к числу, которое и будет значением степени c основанием и иррациональным показателем . В итоге : степень с иррациональным показателем вида можно свести к числу .
Степень положительного числа a с иррациональным показателем записывается как . Его значение – это предел последовательности , где являются последовательными десятичными приближениями иррационального числа . Степень с нулевым основанием можно определить и для положительных иррациональных показателей, при этом Так, . А для отрицательных этого сделать нельзя, поскольку, например, значение не определено. Единица, возведенная в любую иррациональную степень, остается единицей, например, и и будут равны .
Математические онлайн-калькуляторы




