- 16 июля 2025
- 5 минут
- 32 781
Формулы половинного угла в тригонометрии
Статью подготовили специалисты образовательного сервиса Zaochnik.
Формулы половинного угла (аргумента) представляют собой противоположность формулам двойного угла , так как они выражают синус, косинус, тангенс и котангенс угла при помощи тригонометрических функций угла . В статье раскрыты формулы половинного угла и добавлены их доказательства с примерами решений.
Список формул половинного угла
Стандартные формулы половинного угла:
Формулы для и половинного угла справедливы при любом значении заданного угла . Формулу для любого угла определяет , значение угла при равном любому целому числу ( выражение с таким же значением не должно принимать значение ). Формула угла считается справедливой для любого угла , где половинный угол имеет место быть, .
Самые значимые формулы половинного угла для квадратов тригонометрических функций выводятся через положительное или отрицательное значение арифметического квадратного корня. Имеем формулы половинного угла:
Знак «-» указывает, что тригонометрическая функция принадлежит определенной четверти угла .
Применим формулы на практике.
Доказательство формул половинного угла
Доказательство формул половинного угла основывается на формулах двойного угла и . Упростив первое выражение по , получим саму формулу половинного угла , второе выражение по получим .
Чтобы доказать формулы половинного угла для и угла , необходимо применить основные тригонометрические тождества и , к ним необходимо добавить формулы половинного угла и , которые доказали выше. При подстановке получим выражения, имеющие вид:
Все формулы половинного угла были доказаны.
Примеры использования
Покажем применение формул половинного угла при решении примера.
Известно, что . Необходимо вычислить значение градусов, используя формулы половинного угла.
Решение
Данный пример рассматривает применение формулы половинного угла для косинуса, имеющей вид .
Следуя из условия, подставляем числовые значения и получаем: . После получения значения косинуса градусов, необходимо найти само значение косинуса. Для этого вспомним, что угол в градусов принадлежит первой четверти. Там косинус угла имеет положительное значение ( чтобы вспомнить знаки тригонометрических функций, необходимо повторить теорию знаков синуса, косинуса, тангенса и котангенса по четвертям). Следуя из вышесказанного, имеем , тогда . Ответ: .
Применяя формулу половинного угла, стоит учитывать тот факт, что угол может быть не явного вида и , а потребует дальнейшего приведения к стандартному виду. Главное условие – нахождение аргумента в правой части формул половинного угла было в 2 раза больше, чем в левой. Иначе применение формулы будет невозможно.
Если формула позволит записывать данное равенство таким образом или , то формула будет применима.
Для правильного преобразования и применения формул половинного аргумента необходимо досконально изучить свойства тригонометрических функций. Не любое выражение поддается такому преобразованию в тригонометрии. Необходимо внимательно следить за значениями углов тригонометрических функций и их нахождение в четвертях для определения знака для выражения.
Все формулы половинного угла в тригонометрии:
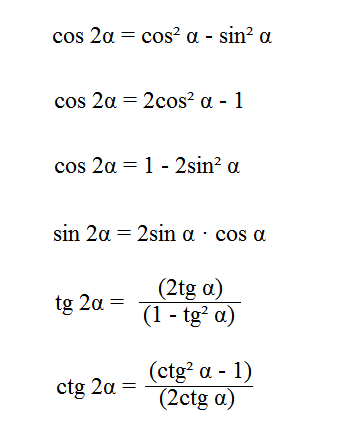
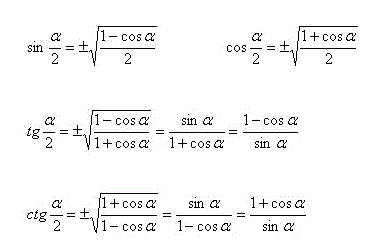
Математические онлайн-калькуляторы




