Формулы приведения: доказательство, примеры, мнемоническое правило

10 декабря 2023
10 минут
4 737

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Данная статья посвящена подробному изучению тригонометрических формул приведения. Дан полный список формул приведения, показаны примеры их использования, приведено доказательство верности формул. Также в статье дано мнемоническое правило, которое позволяет выводить формулы приведения, не запоминая каждую формулу.

Формулы приведения. Список

Фомулы приведения позволяют приводить основные тригонометрические функции углов произвольной величины к функциям углов, лежащих в интервале от $0$ до $90$ градусов (от $0$ до $\frac{π}{2}$ радиан). Оперировать углами от $0$ до $90$ градусов гораздо удобнее, чем работать со сколь угодно большими значениями, поэтому формулы приведения широко применяются при решении задач тригонометрии.

Прежде, чем мы запишем сами формулы, уточним несколько важных для понимания моментов.

Аргументами тригонометрических функций в формулах приведения являются угды вида $\pm α + 2 π \cdot z, \frac{π}{2} \pm α + 2 π \cdot z, \frac{3 π}{2} \pm α + 2 π \cdot z$ . Здесь $z$ - любое целое число, а $α$ - произвольный угол поворота.
Не обязательно учить все формулы приведения, количество которых довольно внушительно. Существует мнемоническое правило, которо позволяет легко вывести нужную формулу. Речь о мнемоническом правиле пойдет позже.

Теперь перейдем непосредственно к формулам приведения.

Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов. запишем все формулы в виде таблицы.

Формулы приведения

$\sin (α + 2 π z) = \sin α, \cos (α + 2 π z) = \cos α t g (α + 2 π z) = t g α, c t g (α + 2 π z) = c t g α \sin (- α + 2 π z) = - \sin α, \cos (- α + 2 π z) = \cos α t g (- α + 2 π z) = - t g α, c t g (- α + 2 π z) = - c t g α \sin (\frac{π}{2} + α + 2 π z) = \cos α, \cos (\frac{π}{2} + α + 2 π z) = - \sin α t g (\frac{π}{2} + α + 2 π z) = - c t g α, c t g (\frac{π}{2} + α + 2 π z) = - t g α \sin (\frac{π}{2} - α + 2 π z) = \cos α, \cos (\frac{π}{2} - α + 2 π z) = \sin α t g (\frac{π}{2} - α + 2 π z) = c t g α, c t g (\frac{π}{2} - α + 2 π z) = t g α \sin (π + α + 2 π z) = - \sin α, \cos (π + α + 2 π z) = - \cos α t g (π + α + 2 π z) = t g α, c t g (π + α + 2 π z) = c t g α \sin (π - α + 2 π z) = \sin α, \cos (π - α + 2 π z) = - \cos α t g (π - α + 2 π z) = - t g α, c t g (π - α + 2 π z) = - c t g α \sin (\frac{3 π}{2} + α + 2 π z) = - \cos α, \cos (\frac{3 π}{2} + α + 2 π z) = \sin α t g (\frac{3 π}{2} + α + 2 π z) = - c t g α, c t g (\frac{3 π}{2} + α + 2 π z) = - t g α \sin (\frac{3 π}{2} - α + 2 π z) = - \cos α, \cos (\frac{3 π}{2} - α + 2 π z) = - \sin α t g (\frac{3 π}{2} - α + 2 π z) = c t g α, c t g (\frac{3 π}{2} - α + 2 π z) = t g α$

В данном случае формулы записаны с радианами. Однако можно записать их и с использованием градусов. Достаточно только перевести радианы в градусы, заменив $π$ на 180 градусов.

Примеры использования формул приведения

Покажем, как пользоваться формулами приведения и как указанные формулы применяются при решении практических примеров.

Угол под знаком тригонометрической функции можно представить не одним, а множеством способов. Например, аргумент тригонометрической функции может быть представлен в видах $\pm α + 2 π z, \frac{π}{2} \pm α + 2 π z, π \pm α + 2 π z, \frac{3 π}{2} \pm α + 2 π z$ . Продемонстрируем это.

Возьмем угол $α = \frac{16 π}{3}$ . Это угол можно записать так:

$α = \frac{16 π}{3} = π + \frac{π}{3} + 2 π \cdot 2 α = \frac{16 π}{3} = - \frac{2 π}{3} + 2 π \cdot 3 α = \frac{16 π}{3} = \frac{3 π}{2} - \frac{π}{6} + 2 π$

В зависимости от представления угла используется соответствующая формула приведения.

Возьмем тот же угол $α = \frac{16 π}{3}$ и вычислим его тангенс

Пример 1. Использование формул приведения

$α = \frac{16 π}{3}, t g α = ?$

Представим угол $α = \frac{16 π}{3}$ в виде $α = π + \frac{π}{3} + 2 π \cdot 2$

Этому представлению угла будет соответствовать формула приведения

$t g (π + α + 2 π z) = t g α$

Получим

$t g \frac{16 π}{3} = t g (π + \frac{π}{3} + 2 π \cdot 2) = t g \frac{π}{3}$

Воспользовавшись таблицей, укажем значение тангенса

$t g \frac{π}{3} = \sqrt{3}$

Теперь используем другое представление угла $α = \frac{16 π}{3}$ .

Пример 2. Использование формул приведения

$α = \frac{16 π}{3}, t g α = ? α = - \frac{2 π}{3} + 2 π \cdot 3 t g \frac{16 π}{3} = t g (- \frac{2 π}{3} + 2 π \cdot 3) = - t g \frac{2 π}{3} = - (- \sqrt{3}) = \sqrt{3}$

Наконец, для третьего представления угла запишем

Пример 3. Использование формул приведения

$α = \frac{16 π}{3} = \frac{3 π}{2} - \frac{π}{6} + 2 π t g (\frac{3 π}{2} - α + 2 π z) = c t g α t g α = t g (\frac{3 π}{2} - \frac{π}{6} + 2 π) = c t g \frac{π}{6} = \sqrt{3}$

Теперь приведем пример на использование формул приведения посложнее

Пример 4. Использование формул приведения

Представим $\sin 197 °$ через синус и косинус острого угла.

Для того, чтобы можно было применять формулы приведения, нужно представить угол $α = 197 °$ в одном из видов

$\pm α + 360 ° \cdot z, 90 ° \pm α + 360 ° \cdot z, 180 ° \pm α + 360 ° \cdot z, 270 ° \pm α + 360 ° \cdot z$ . Согласно условию задачи, угол должен быть острым. Соответственно, у нас есть два способа для его представления:

$197 ° = 180 ° + 17 ° 197 ° = 270 ° - 73 °$

Получаем

$\sin 197 ° = \sin (180 ° + 17 °) \sin 197 ° = \sin (270 ° - 73 °)$

Теперь посмотрим на формулы приведения для синусов и выберем соответствующие

$\sin (π + α + 2 πz) = - sinα \sin (\frac{3 π}{2} - α + 2 πz) = - cosα \sin 197 ° = \sin (180 ° + 17 ° + 360 ° \cdot z) = - \sin 17 ° \sin 197 ° = \sin (270 ° - 73 ° + 360 ° \cdot z) = - \cos 73 °$

Мнемоническое правило

Формул приведения много, и, к счастью, нет необходимости заучивать их наизусть. Существуют закономерности, по которым можно выводить формулы приведения для разных углов и тригонометрических функций. Эти закономерности называются мнемоническим правилом. Мнемоника - искусство запоминания. Мнемоническое правило состоит из трех частей, или содержит три этапа.

Мнемоническое правило

1. Аргумент исходной функции представляется в одном из видов

$\pm α + 2 πz \frac{π}{2} \pm α + 2 πz π \pm α + 2 πz \frac{3 π}{2} \pm α + 2 πz$

Угол $α$ должен лежать в пределах от 0 до 90 градусов.

2. Определяется знак исходной тригонометрической функции. Такой же знак будет иметь функция, записываемая в правой части формулы.

3. Для углов $\pm α + 2 πz$ и $π \pm α + 2 πz$ название исходной функции остается неизменным, а для углов $\frac{π}{2} \pm α + 2 πz$ и $\frac{3 π}{2} \pm α + 2 πz$ соответственно меняется на "кофункцию". Синус - на косинус. Тангенс - на котангенс.

Чтобы пользоваться мнемоническим праилом для формул приведения нужно уметь определять знаки тригонометрических функций по четвертям единичной окружности. Разберем примеры применения мнемонического правила.

Пример 1. Использование мнемонического правила

Запишем формулы приведения для $\cos (\frac{π}{2} - α + 2 πz)$ и $t g (π - α + 2 πz)$ . $α$ - улог первой четверти.

1. Так как по условию $α$ - улог первой четверти, мы пропускаем первый пункт правила.

2. Определим знаки функций $\cos (\frac{π}{2} - α + 2 πz)$ и $t g (π - α + 2 πz)$ . Угол $\frac{π}{2} - α + 2 πz$ также является углом первой четверти, а угол $π - α + 2 πz$ находится во второй четверти. В первой четверти функция косинуса положительна, а тангенс во второй четверти имеет знак минус. Запишем, как будут выглядеть искомые формулы на этом этапе.

$\cos (\frac{π}{2} - α + 2 πz) = + t g (π - α + 2 πz) = -$

3. Согласно третьему пункту для угла $\frac{π}{2} - α + 2 π$ название функции изменяется на конфуцию, а для угла $π - α + 2 πz$ остается прежним. Запишем:

$\cos (\frac{π}{2} - α + 2 πz) = + \sin α t g (π - α + 2 πz) = - t g α$

А теперь заглянем в формулы, приведенные выше, и убедимся в том, что мнемоническое правило работает.

Рассмотрим пример с конкретным углом $α = 777 °$ . Приведем синус альфа к тригонометрической функции острого угла.

Пример 2. Использование мнемонического правила

1. Представим углол $α = 777 °$ в необходимом виде

$777 ° = 57 ° + 360 ° \cdot 2 777 ° = 90 ° - 33 ° + 360 ° \cdot 2$

2. Исходный угол - угол первой четверти. Значит, синус угла имеет положительный знак. В итоге имеем:

3. $\sin 777 ° = \sin (57 ° + 360 ° \cdot 2) = \sin 57 ° \sin 777 ° = \sin (90 ° - 33 ° + 360 ° \cdot 2) = \cos 33 °$

Теперь рассмотрим пример, который показывает, как важно правильно определить знак тригонометрической функции и правильно представить угол при использовании мнемонического правила. Повторим еще раз.

Важно!

Угол $α$ должен быть острым!

Вычислим тангенс угла $\frac{5 π}{3}$ . Из таблицы значений основных тригонометрических функций можно сразу взять значение $t g \frac{5 π}{3} = - \sqrt{3}$ , но мы применим мнемоническое правило.

Пример 3. Использование мнемонического правила

$t g \frac{5 π}{3} = ?$

Представим угол $α = \frac{5 π}{3}$ в необходимом виде и воспользуемся правилом

$t g \frac{5 π}{3} = t g (\frac{3 π}{2} + \frac{π}{6}) = - c t g \frac{π}{6} = - \sqrt{3} t g \frac{5 π}{3} = t g (2 π - \frac{π}{3}) = - t g \frac{π}{3} = - \sqrt{3}$

Если же представить угол альфа в виде $\frac{5 π}{3} = π + \frac{2 π}{3}$ , то результат применениея мнемонического правила будет неверным.

$t g \frac{5 π}{3} = t g (π + \frac{2 π}{3}) = - t g \frac{2 π}{3} = - (- \sqrt{3}) = \sqrt{3}$

Неверный результат обусловлен тем, что угол $\frac{2 π}{3}$ не явдяется острым.

Формулы приведения. Доказательство

Доказательство формул приведения основывается на свойствах периодичности и симметричности тригонометрических функций, а также на свойстве сдвига на углы $\frac{π}{2}$ и $\frac{3 π}{2}$ . Доказательство справедливости всех формул приведения иожно проводить без учета слагаемого $2 πz$ , так как оно обозначает изменение угла на целое число полных оборотов и как раз отражает свойство периодичности.

Первые 16 формул следуют напрямую из свойств основных тригонометрических функций: синуса, косинуса, тангенса и котанганса.

Приведем доказательство формул приведения для синусов и косинусов

$\sin (\frac{π}{2} + α) = \cos α$ и $\cos (\frac{π}{2} + α) = - \sin α$

Посмотрим на единичную окружность, начальная точка которой после повоторота на угол $α$ перешла в точку $A_{1} (x, y)$ , а после поворота на угол $\frac{π}{2} + α$ - в точку $A_{2}$ . Из обеих точек проведем перпендикуляры к оси абсцисс.

Формулы приведения. Доказательство

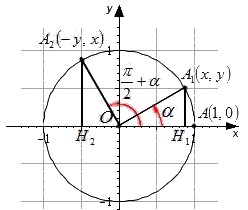
Два прямоугольных треугольника $O A_{1} H_{1}$ и $O A_{2} H_{2}$ равны по гипотенузе и прилежащим к ней углам. Из расположения точек на окружности и равенства треугольников можно сделать вывод о том, что точка $A_{2}$ имеет координаты $A_{2} (- y, x)$ . Используя определения синуса и косинуса, запишем:

$\sin α = y, \cos α = x, \sin (\frac{π}{2} + α) = x, \cos (\frac{π}{2} + α) = y$

Отсюда

$\sin (\frac{π}{2} + α) = \cos α, \cos (\frac{π}{2} + α) = - \sin α$

С учетом основных тождеств тригонометрии и только что доказанного, можно записать

$t g (\frac{π}{2} + α) = \frac{\sin (\frac{π}{2} + α)}{\cos (\frac{π}{2} + α)} = \frac{\cos α}{- \sin α} = - c t g α c t g (\frac{π}{2} + α) = \frac{\cos (\frac{π}{2} + α)}{\sin (\frac{π}{2} + α)} = \frac{- \sin α}{\cos α} = - t g α$

Для доказательства формул приведения с аргументом $\frac{π}{2} - α$ его необходимо представить в виде $\frac{π}{2} + (- α)$ . Например:

$\cos (\frac{π}{2} - α) = \cos (\frac{π}{2} + (- α)) = - \sin (- α) = \sin α$

В доказательстве используются свойства тригонометрических функций с аргументами, противоположными по знаку.

Все остальные формулы приведения можно доказать на базе записанных выше.