Формулы сложения: доказательство, примеры

Содержание:

21 октября 2023
10 минут
3835

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Продолжаем наш разговор про наиболее употребляемые формулы в тригонометрии. Важнейшие из них – формулы сложения.

Определение 1

Формулы сложения позволяют выразить функции разности или суммы двух углов с помощью тригонометрических функций этих углов.

Для начала мы приведем полный список формул сложения, потом докажем их и разберем несколько наглядных примеров.

Основные формулы сложения в тригонометрии

Выделяют восемь основных формул: синус суммы и синус разности двух углов, косинусы суммы и разности, тангенсы и котангенсы суммы и разности соответственно. Ниже приведены их стандартные формулировки и вычисления.

1.Синус суммы двух углов можно получить следующим образом:

- вычисляем произведение синуса первого угла на косинус второго;

- умножаем косинус первого угла на синус первого;

- складываем получившиеся значения.

Графическое написание формулы выглядит так: $\sin (α + β) = \sin α \cdot \cos β + \cos α \cdot \sin β$

2. Синус разности вычисляется почти так же, только полученные произведения нужно не сложить, а вычесть друг из друга. Таким образом, вычисляем произведения синуса первого угла на косинус второго и косинуса первого угла на синус второго и находим их разность. Формула пишется так: $\sin (α - β) = \sin α \cdot \cos β + \sin α \cdot \sin β$

3. Косинус суммы. Для него находим произведения косинуса первого угла на косинус второго и синуса первого угла на синус второго соответственно и находим их разность: $\cos (α + β) = \cos α \cdot \cos β - \sin α \cdot \sin β$

4. Косинус разности: вычисляем произведения синусов и косинусов данных углов, как и ранее, и складываем их. Формула: $\cos (α - β) = \cos α \cdot \cos β + \sin α \cdot \sin β$

5. Тангенс суммы. Эта формула выражается дробью, в числителе которой – сумма тангенсов искомых углов, а в знаменателе – единица, из которой вычитается произведение тангенсов искомых углов. Все понятно из ее графической записи: $t g (α + β) = \frac{t g α + t g β}{1 - t g α \cdot t g β}$

6. Тангенс разности. Вычисляем значения разности и произведения тангенсов данных углов и поступаем с ними схожим образом. В знаменателе мы прибавляем к единице, а не наоборот: $t g (α - β) = \frac{t g α - t g β}{1 + t g α \cdot t g β}$

7. Котангенс суммы. Для вычислений по этой формуле нам понадобятся произведение и сумма котангенсов данных углов, с которыми мы поступаем следующим образом: $c t g (α + β) = \frac{- 1 + c t g α \cdot c t g β}{c t g α + c t g β}$

8. Котангенс разности. Формула схожа с предыдущей, но в числителе и знаменателе – минус, а не плюс $c t g (α - β) = \frac{- 1 - c t g α \cdot c t g β}{c t g α - c t g β}$ .

Вы, наверное, заметили, что эти формулы попарно схожи. При помощи знаков $\pm$ (плюс-минус) и $\mp$ (минус-плюс) мы можем сгруппировать их для удобства записи:

$\sin (α \pm β) = \sin α \cdot \cos β \pm \cos α \cdot \sin β \cos (α \pm β) = \cos α \cdot \cos β \mp \sin α \cdot \sin β t g (α \pm β) = \frac{t g α \pm t g β}{1 \mp t g α \cdot t g β} c t g (α \pm β) = \frac{- 1 \pm c t g α \cdot c t g β}{c t g α \pm c t g β}$

Соответственно, мы имеем одну формулу записи для суммы и разности каждого значения, просто в одном случае мы обращаем внимание на верхний знак, в другом – на нижний.

Определение 2

Мы можем взять любые углы $α$ и $β$ , и формулы сложения для косинуса и синуса подойдут для них. Если мы можем правильно определить значения тангенсов и котангенсов этих углов, то формулы сложения для тангенса и котангенса будут также для них справедливы.

Доказательства формул сложения

Как и большинство понятий в алгебре, формулы сложения могут быть доказаны. Первая формула, которую мы докажем, - формула косинуса разности. Из нее потом можно легко вывести остальные доказательства.

Уточним основные понятия. Нам понадобится единичная окружность. Она получится, если мы возьмем некую точку $A$ и повернем вокруг центра (точки $O$ ) углы $α$ и $β$ . Тогда угол между векторами $\vec{O A_{1}}$ и ${\vec{O A}}_{2}$ будет равняться $(α - β) + 2 π \cdot z$ или $2 π - (α - β) + 2 π \cdot z$ ( $z$ – любое целое число). Получившиеся вектора образуют угол, который равен $α - β$ или $2 π - (α - β)$ , или он может отличаться от этих значений на целое число полных оборотов. Взгляните на рисунок:

Доказательства формул сложения

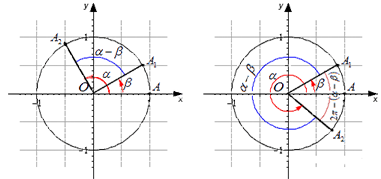
Мы воспользовались формулами приведения и получили следующие результаты:

$\cos ((α - β) + 2 π \cdot z) = \cos (α - β) \cos (2 π - (α - β) + 2 π \cdot z) = \cos (α - β)$

Итог: косинус угла между векторами $\vec{O A_{1}}$ и $\vec{O A_{2}}$ равняется косинусу угла $α - β$ , следовательно, $\cos (\vec{O A_{1}} \vec{O A_{2}}) = \cos (α - β)$ .

Далее мы переходим к самому доказательству формулы косинуса разности.

Вспомним определения синуса и косинуса: синус - функция угла, равная отношению катета противолежащего угла к гипотенузе, косинус – это синус дополнительного угла. Следовательно, точки $A_{1}$ и $A_{2}$ имеют координаты $(\cos α, \sin α)$ и $(\cos β, \sin β)$ .

Получим следующее:

$\vec{O A_{1}} = (\cos α, \sin α)$ и $\vec{O A_{2}} = (\cos β, \sin β)$

Если непонятно, взгляните на координаты точек, расположенных в начале и конце векторов.

Длины векторов равны $1$ , т.к. у нас единичная окружность.

Разберем теперь скалярное произведение векторов $\vec{O A_{1}}$ и $\vec{O A_{2}}$ . В координатах оно выглядит так:

$(\vec{O A_{1}}, \vec{O A_{2})} = \cos α \cdot \cos β + \sin α \cdot \sin β$

Из этого мы можем вывести равенство:

$\cos (α - β) = \cos α \cdot \cos β + \sin α \cdot \sin β$

Таким образом, формула косинуса разности доказана.

Теперь мы докажем следующую формулу – косинуса суммы. Это проще, поскольку мы можем воспользоваться предыдущими расчетами. Возьмем представление $α + β = α - (- β)$ . У нас есть:

$\cos (α + β) = \cos (α - (- β)) = = \cos α \cdot \cos (- β) + \sin α \cdot \sin (- β) = = \cos α \cdot \cos β + \sin α \cdot \sin β$

Это и есть доказательство формулы косинуса суммы. В последней строчке использовано свойство синуса и косинуса противоположных углов.

Формулу синуса суммы можно вывести из формулы косинуса разности. Возьмем для этого формулу приведения:

вида $\sin (α + β) = \cos (\frac{π}{2} (α + β))$ . Так
$\sin (α + β) = \cos (\frac{π}{2} (α + β)) = \cos ((\frac{π}{2} - α) - β) = = \cos (\frac{π}{2} - α) \cdot \cos β + \sin (\frac{π}{2} - α) \cdot \sin β = = \sin α \cdot \cos β + \cos α \cdot \sin β$

А вот доказательство формулы синуса разности:

$\sin (α - β) = \sin (α + (- β)) = \sin α \cdot \cos (- β) + \cos α \cdot \sin (- β) = = \sin α \cdot \cos β - \cos α \cdot \sin β$
Обратите внимание на использование свойств синуса и косинуса противоположных углов в последнем вычислении.

Далее нам нужны доказательства формул сложения для тангенса и котангенса. Вспомним основные определения (тангенс – отношение синуса к косинусу, а котангенс –наоборот) и возьмем уже выведенные заранее формулы. У нас получилось:

$t g (α + β) = \frac{\sin (α + β)}{\cos (α + β)} = \frac{\sin α \cdot \cos β + \cos α \cdot \sin β}{\cos α \cdot \cos β - \sin α \cdot \sin β}$

У нас получилась сложная дробь. Далее нам нужно разделить ее числитель и знаменатель на $\cos α \cdot \cos β$ , учитывая что $\cos α \neq 0$ и $\cos β \neq 0$ , получаем:
$\frac{\frac{\sin α \cdot \cos β + \cos α \cdot \sin β}{\cos α \cdot \cos β}}{\frac{\cos α \cdot \cos β - \sin α \cdot \sin β}{\cos α \cdot \cos β}} = \frac{\frac{\sin α \cdot \cos β}{\cos α \cdot \cos β} + \frac{\cos α \cdot \sin β}{\cos α \cdot \cos β}}{\frac{\cos α \cdot \cos β}{\cos α \cdot \cos β} - \frac{\sin α \cdot \sin β}{\cos α \cdot \cos β}}$

Теперь сокращаем дроби и получаем формулу следующего вида: $\frac{\frac{\sin α}{\cos α} + \frac{\sin β}{\cos β}}{1 - \frac{\sin α}{\cos α} \cdot \frac{s i n β}{\cos β}} = \frac{t g α + t g β}{1 - t g α \cdot t g β}$ .
У нас получилось $t g (α + β) = \frac{t g α + t g β}{1 - t g α \cdot t g β}$ . Это и есть доказательство формулы сложения тангенса.

Следующая формула, которую мы будем доказывать – формула тангенса разности. Все наглядно показано в вычислениях:

$t g (α - β) = t g (α + (- β)) = \frac{t g α + t g (- β)}{1 - t g α \cdot t g (- β)} = \frac{t g α - t g β}{1 + t g α \cdot t g β}$

Формулы для котангенса доказываются схожим образом:
$c t g (α + β) = \frac{\cos (α + β)}{\sin (α + β)} = \frac{\cos α \cdot \cos β - \sin α \cdot \sin β}{\sin α \cdot \cos β + \cos α \cdot \sin β} = = \frac{\frac{\cos α \cdot \cos β - \sin α \cdot \sin β}{\sin α \cdot \sin β}}{\frac{\sin α \cdot \cos β + \cos α \cdot \sin β}{\sin α \cdot \sin β}} = \frac{\frac{\cos α \cdot \cos β}{\sin α \cdot \sin β} - 1}{\frac{\sin α \cdot \cos β}{\sin α \cdot \sin β} + \frac{\cos α \cdot \sin β}{\sin α \cdot \sin β}} = = \frac{- 1 + c t g α \cdot c t g β}{c t g α + c t g β}$
Далее:
$c t g (α - β) = c t g (α + (- β)) = \frac{- 1 + c t g α \cdot c t g (- β)}{c t g α + c t g (- β)} = \frac{- 1 - c t g α \cdot c t g β}{c t g α - c t g β}$

Примеры сложения с помощью тригонометрических формул

В этом пункте мы рассмотрим, как применить эти сложные на вид вычисления на практике. Их можно использовать:

- при преобразовании тригонометрических выражений;

- для вычисления точных значений синуса, косинуса, тангенса и котангенса углов, которые отличаются от основных ( $0, \frac{π}{6}, \frac{π}{4}, \frac{π}{3}, \frac{π}{2}$ );

- для доказательства других тригонометрических формул, например, формулы двойного угла.

Разберем задачи с использованием формул сложения.

Пример 1

Задача: Вычислите точное значение тангенса $15$ градусов.

Решение

Для наглядности мы $15$ градусов можно представить в виде разности $45 - 30$ . В этом случае решение задачи можно получить с помощью формулы тангенса разности. Возьмем формулу, которую мы приводили выше, и укажем в ней имеющиеся нам известные значения: $t g 15 ° = t g (45 ° - 30 °) = \frac{t g 45 ° - t g 30 °}{1 + t g 45 ° \cdot t g 30 °}$

Вычисляем ответ: $\frac{t g 45 ° - t g 30 °}{1 + t g 45 ° \cdot t g 30 °} = \frac{1 - \frac{\sqrt{3}}{3}}{1 + 1 \cdot \frac{\sqrt{3}}{3}} = = \frac{\sqrt{3} - 1}{\sqrt{3} + 1} = \frac{(\sqrt{3} - 1) \cdot (\sqrt{3} - 1)}{(\sqrt{3} + 1) \cdot (\sqrt{3} - 1)} = \frac{(\sqrt{3})^{2} - 2 \sqrt{3} + 1}{(\sqrt{3})^{2} - 1} = 2 - \sqrt{3}$

Ответ: $t g 15 ° = 2 - \sqrt{3}$

Пример 2

Задача: Выберем формулу сложения для проверки формулы приведения следующего вида: $\sin (\frac{π}{2} + α) = \cos α$

Нам подойдет формула синуса суммы. Итого: $\sin (\frac{π}{2} + α) = \sin \frac{π}{2} \cdot \cos α + \cos \frac{π}{2} \cdot \sin α = 1 \cdot \cos α + 0 \cdot \sin α = \cos α$

Ответ: $\sin (\frac{π}{2} + α) = \cos α$ - наша формула доказана.

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.