Основные тригонометрические тождества: их формулировки и вывод

В статье подробно рассказывается об основных тригонометрических тождествах.Эти равенства устанавливают связь между $\sin , \cos , tg, ctg$ заданного угла. При известной одной функции можно через нее найти другую.

Тригонометрические тождества для рассмотрения в денной статье. Ниже покажем пример их выведения с объяснением.

$$\begin{gathered} {\sin }^2\alpha +{\cos }^2\alpha =1 \\ tg \alpha =\frac{\sin \alpha }{\cos \alpha }, ctg \alpha =\frac{\cos \alpha }{\sin \alpha } \\ tg \alpha ·ctg \alpha =1 \\ t{g}^2\alpha +1=\frac{1}{{\cos }^2\alpha }, 1+ct{g}^2\alpha =\frac{1}{{\sin }^2\alpha } \end{gathered}$$

Связь между sin и cos одного угла

Поговорим о важном тригонометрическом тождестве, которое считается основой основ в тригонометрии.

${\sin }^2\alpha +{\cos }^2\alpha =1$

Заданные равенства $t{g}^2\alpha +1=\frac{1}{{\cos }^2\alpha }, 1+ct{g}^2\alpha =\frac{1}{{\sin }^2\alpha }$ выводят из основного путем деления обеих частей на ${\sin }^2\alpha$ и ${\cos }^2\alpha$. После чего получаем $tg \alpha =\frac{\sin \alpha }{\cos \alpha }, ctg \alpha =\frac{\cos \alpha }{\sin \alpha }$ и $tg \alpha ·ctg \alpha =1$ - это следствие определений синуса, косинуса, тангенса и котангенса.

Равенство ${\sin }^2\alpha +{\cos }^2\alpha =1$ является основным тригонометрическим тождеством. Для его доказательства необходимо обратиться к теме с единичной окружностью .

Пусть даны координаты точки $А(1,0)$, которая после поворота на угол $\alpha$становится в точку ${А}_1$. По определению $\sin$ и $\cos$ точка ${А}_1$ получит координаты $(\cos \alpha , \sin \alpha )$. Так как ${А}_1$ находится в пределах единичной окружности, значит, координаты должны удовлетворят условию $x^2+y^2=1$ этой окружности. Выражение ${\cos }^2\alpha +{\sin }^2\alpha =1$ должно быть справедливым. Для этого необходимо доказать основное тригонометрическое тождество для всех углов поворота $\alpha$.

В тригонометрии выражение ${\sin }^2\alpha +{\cos }^2\alpha =1$ применяют как теорему Пифагора в тригонометрии. Для этого рассмотрим подробное доказательство.

Используя единичную окружность, поворачиваем точку $А$ с координатами $(1,0)$ вокруг центральной точки $О$ на угол $\alpha$. После поворота точка меняет координаты и становится равной ${А}_1(х,у)$. Опускаем перпендикулярную прямую ${А}_1Н$ на $Ох$ из точки ${А}_1$.

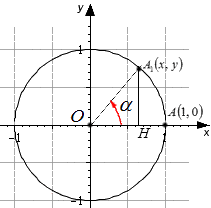
На рисунке отлично видно, что образовался прямоугольный треугольник $О{А}_1Н$. По модулю катеты $О{А}_1Н$ и $ОН$ равные, запись примет такой вид: $\left|{А}_{1}H\right|=\left|у\right|,\left|ОН\right|=\left|х\right|$. Гипотенуза $О{А}_1$ имеет значение равное радиусу единичной окружности, $\left|О{А}_1\right|=1$. Используя данное выражение, можем записать равенство по теореме Пифагора: $|{А}_1Н{|}^2 +|ОН{|}^2 =|О{А}_1{|}^2$. Это равенство запишем как$|y{|}^2+|x{|}^2=1^2$, что означает $y^2+x^2=1$.

Используя определение $\sin \alpha =y$ и $\cos \alpha =x$, подставим данные угла вместо координат точек и перейдем к неравенству ${\sin }^2\alpha +{\cos }^2\alpha =1$.

Основная связь между $\sin$ и $\cos$ угла возможна через данное тригонометрическое тождество. Таким образом, можно считать sin угла с известным cos и наоборот. Чтобы выполнить это, необходимо разрешать ${\sin }^2\alpha +{\cos }^2=1$ относительно $\sin$ и $\cos$, тогда получим выражения вида $\sin \alpha =\pm \sqrt{1-{\cos }^2\alpha }$ и $\cos \alpha =\pm \sqrt{1-{\sin }^2\alpha }$ соответственно. Величина угла $\alpha$определяет знак перед корнем выражения. Для подробного выяснения необходимо прочитать раздел вычисление синуса, косинуса, тангенса и котангенса с использованием тригонометрических формул.

Чаще всего основную формулу применяют для преобразований или упрощений тригонометрических выражений. Имеется возможность заменять сумму квадратов синуса и косинуса на $1$. Подстановка тождества может быть как в прямом, так и обратном порядке: единицу заменяют на выражение суммы квадратов синуса и косинуса.

Тангенс и котангенс через синус и косинус

Из определения косинуса и синуса, тангенса и котангенса видно, что они взаимосвязаны друг с другом, что позволяет отдельно преобразовывать необходимые величины.

$$\begin{gathered} tg \alpha =\frac{\sin \alpha }{\cos \alpha } \\ ctg \alpha =\frac{\cos \alpha }{\sin \alpha } \end{gathered}$$

Из определения синус является ординатой $у$, а косинус – абсциссой $x$. Тангенс – это и есть отношения ординаты и абсциссы. Таким образом имеем:

$tg \alpha =\frac{y}{x}=\frac{\sin \alpha }{\cos \alpha }$, а выражение котангенса имеет обратное значение, то есть

$ctg \alpha =\frac{x}{y}=\frac{\cos \alpha }{\sin \alpha }$.

Отсюда следует, что полученные тождества $tg \alpha =\frac{\sin \alpha }{\cos \alpha }$ и $ctg \alpha =\frac{\cos \alpha }{\sin \alpha }$ задаются с помощью $\sin$ и $\cos$ углов. Тангенс считаются отношением синуса к косинусу угла между ними, а котангенс наоборот.

Отметим, что $tg \alpha =\frac{\sin \alpha }{\cos \alpha }$ и $ctg \alpha =\frac{\cos \alpha }{\sin \alpha }$ верны для любого значение угла $\alpha$, значения которого входят в диапазон. Из формулы $tg \alpha =\frac{\sin \alpha }{\cos \alpha }$ значение угла $\alpha$ отлично от $\frac{\pi }{2}+\pi ·z$, а $ctg \alpha =\frac{\cos \alpha }{\sin \alpha }$ принимает значение угла $\alpha$, отличные от $\mathrm{\pi }·\mathrm{z}$, $z$ принимает значение любого целого числа.

Связь между тангенсом и котангенсом

Имеется формула, которая показывает связь между углами через тангенс и котангенс. Данное тригонометрическое тождество является важным в тригонометрии и обозначается как $tg \alpha ·ctg \alpha =1$. Оно имеет смысл при $\alpha$ с любым значением, кроме $\frac{\pi }{2}·z$, иначе функции будут не определены.

Формула $tg \alpha ·ctg \alpha =1$ имеет свои особенности в доказательстве. Из определения мы имеем, что $tg \alpha =\frac{y}{x}$ и $ctg \alpha =\frac{x}{y}$, отсюда получаем $tg \alpha ·ctg \alpha =\frac{y}{x}·\frac{x}{y}=1$. Преобразовав выражение и подставив $tg \alpha =\frac{\sin \alpha }{\cos \alpha }$ и $ctg \alpha =\frac{\cos \alpha }{\sin \alpha }$, получим $tg \alpha ·ctg \alpha =\frac{\sin \alpha }{\cos \alpha }·\frac{\cos \alpha }{\sin \alpha }=1$.

Тогда выражение тангенса и котангенса имеет смысл того, когда в итоге получаем взаимно обратные числа.

Тангенс и косинус, котангенс и синус

Преобразовав основные тождества, приходим к выводу, что тангенс связан через косинус, а котангенс через синус. Это видно по формулам $t{g}^2\alpha +1=\frac{1}{{\cos }^2\alpha }, 1+ct{g}^2\alpha =\frac{1}{{\sin }^2\alpha }$.

Определение звучит так: сумма квадрата тангенса угла и $1$ приравнивается к дроби , где в числителе имеем $1$, а в знаменателе квадрат косинуса данного угла, а сумма квадрата котангенса угла наоборот. Благодаря тригонометрическому тождеству ${\sin }^2\alpha +{\cos }^2\alpha =1$, можно разделить соответствующие стороны на ${\cos }^2\alpha$ и получить $t{g}^2\alpha +1=\frac{1}{{\cos }^2\alpha }$, где значение ${\cos }^2\alpha$ не должно равняться нулю. При делении на ${\sin }^2\alpha$ получим тождество $1+ct{g}^2\alpha =\frac{1}{{\sin }^2\alpha }$, где значение ${\sin }^2\alpha$ не должно равняться нулю.

Из приведенных выражений получили, что тождество $t{g}^2\alpha +1=\frac{1}{{\cos }^2\alpha }$ верно при всех значениях угла $\alpha$, не принадлежащих $\frac{\pi }{2}+\pi ·z$, а $1+ct{g}^2\alpha =\frac{1}{{\sin }^2\alpha }$ при значениях $\alpha$, не принадлежащих промежутку $\pi ·z$.