Свойства синуса, косинуса, тангенса и котангенса

21 мая 2023
6 минут
6 914

Содержание:

Знаки тригонометрических функций по четвертям
Свойство периодичности
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.

Первое свойство - знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол $α$ $α$ . Второе свойство - периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах $α$ $α$ и $- α$ $- α$ .

Знаки тригонометрических функций по четвертям

Часто в математическом тексте или в контексте задачи можно встретить фразу: "угол первой, второй, третьей или четвертой координатной четверти". Что это такое?

Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку $A_{0} (1, 0)$ $A_{0} (1, 0)$ и, поворачивая ее вокруг точки $O$ $O$ на угол $α$ $α$ , попадем в точку $A_{1} (x, y)$ $A_{1} (x, y)$ . В зависимости от того, в какой четверти будет лежать точка $A_{1} (x, y)$ $A_{1} (x, y)$ , угол $α$ $α$ будет называться углом первой, второй, третьей и четвертой четвети соответственно.

Для наглядности приведем иллюстрацию.

Знаки тригонометрических функций по четвертям

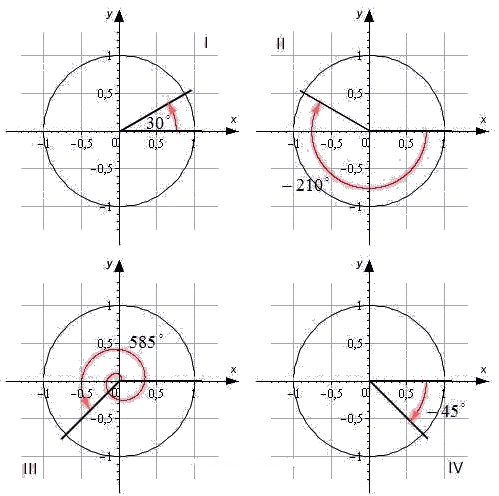
Угол $α = 30 °$ $α = 30 °$ лежит в первой четверти. Угол $- 210 °$ $- 210 °$ является углом второй четверти. Угол $585 °$ $585 °$ - угол третьей четверти. Угол $- 45 °$ $- 45 °$ - это угол четвертой четверти.

При этом углы $\pm 90 °, \pm 180 °, \pm 270 °, \pm 360 °$ $\pm 90 °, \pm 180 °, \pm 270 °, \pm 360 °$ не принадлежат ни одной четверти, так как лежат на координатных осях.

Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.

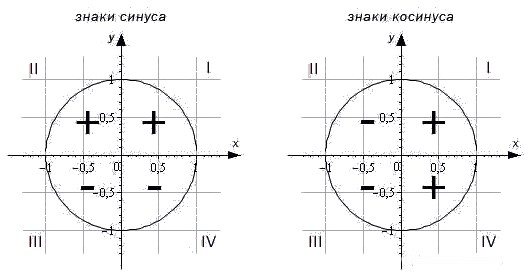
Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус - это ордината точки $A_{1} (x, y)$ $A_{1} (x, y)$ . Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной - отрицательна.

Косинус - это абсцисса точки $A_{1} (x, y)$ $A_{1} (x, y)$ . В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.

Знаки тригонометрических функций по четвертям

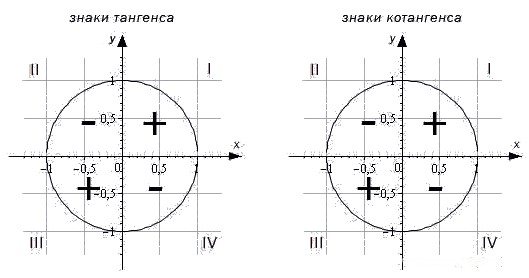
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс - отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки - отрицательным. Аналогично определяются знаки котангенса по четвертям.

Знаки тригонометрических функций по четвертям

Важно помнить!

Синус угла $α$ $α$ имеет знак плюс в 1 и 2 четвертях, знак минус - в 3 и 4 четвертях.
Косинус угла $α$ $α$ имеет знак плюс в 1 и 4 четвертях, знак минус - в 2 и 3 четвертях.
Тангенс угла $α$ $α$ имеет знак плюс в 1 и 3 четвертях, знак минус - в 2 и 4 четвертях.
Котангенс угла $α$ $α$ имеет знак плюс в 1 и 3 четвертях, знак минус - в 2 и 4 четвертях.

Свойство периодичности

Свойство периодичности - одно из самых очевидных свойств тригонометрических функций.

Свойство периодичности

При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.

Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки $A$ $A$ на единичной окружности в точку $A_{1}$ $A_{1}$ с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.

Математически данное свойство записывается так:

$sin (α + 2 π \cdot z) = sin α cos (α + 2 π \cdot z) = cos α t g (α + 2 π \cdot z) = t g α c t g (α + 2 π \cdot z) = c t g α$ $\sin (α + 2 π \cdot z) = \sin α \cos (α + 2 π \cdot z) = \cos α t g (α + 2 π \cdot z) = t g α c t g (α + 2 π \cdot z) = c t g α$

Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.

Приведем примеры.

$sin \frac{13 π}{5} = sin (\frac{3 π}{5} + 2 π) = sin \frac{3 π}{5}$ $\sin \frac{13 π}{5} = \sin (\frac{3 π}{5} + 2 π) = \sin \frac{3 π}{5}$

$t g (- 689 °) = t g (31 ° + 360 ° \cdot (- 2)) = t g 31 ° t g (- 689 °) = t g (- 329 ° + 360 ° \cdot (- 1)) = t g (- 329 °)$ $t g (- 689 °) = t g (31 ° + 360 ° \cdot (- 2)) = t g 31 ° t g (- 689 °) = t g (- 329 ° + 360 ° \cdot (- 1)) = t g (- 329 °)$

Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов

Вновь обратимся к единичной окружности.

Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов

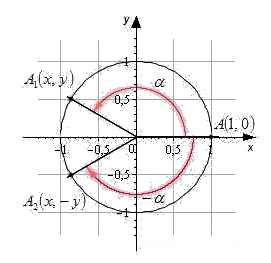
Точка $A_{1} (x, y)$ $A_{1} (x, y)$ - результат поворота начальной точки $A_{0} (1, 0)$ $A_{0} (1, 0)$ вокруг центра окружности на угол $α$ $α$ . Точка $A_{2} (x, - y)$ $A_{2} (x, - y)$ - результат поворота начальной точки на угол $- α$ $- α$ .

Точки $A_{1}$ $A_{1}$ и $A_{2}$ $A_{2}$ симметричны относительно оси абсцисс. В случае, когда $α = 0 °, \pm 180 °, \pm 360 °$ $α = 0 °, \pm 180 °, \pm 360 °$ точки $A_{1}$ $A_{1}$ и $A_{2}$ $A_{2}$ совпадают. Пусть одна точка имеет координаты $(x, y)$ $(x, y)$ , а вторая - $(x, - y)$ $(x, - y)$ . Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:

$sin α = y, cos α = x, t g α = \frac{y}{x}, c t g α = \frac{x}{y} sin (- α) = - y, cos (- α) = x, t g (- α) = \frac{- y}{x}, c t g (- α) = \frac{x}{- y}$ $\sin α = y, \cos α = x, t g α = \frac{y}{x}, c t g α = \frac{x}{y} \sin (- α) = - y, \cos (- α) = x, t g (- α) = \frac{- y}{x}, c t g (- α) = \frac{x}{- y}$

Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.

Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов

$sin (- α) = - sin α cos (- α) = cos α t g (- α) = - t g α c t g (- α) = - c t g α$ $\sin (- α) = - \sin α \cos (- α) = \cos α t g (- α) = - t g α c t g (- α) = - c t g α$

Согласно этому свойству, справедливы равенства

$sin (- 48 °) = - sin 48 °, c t g \frac{π}{9} = - c t g (- \frac{π}{9}), cos 18 ° = cos (- 18 °)$ $\sin (- 48 °) = - \sin 48 °, c t g \frac{π}{9} = - c t g (- \frac{π}{9}), \cos 18 ° = \cos (- 18 °)$

Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter