Прямоугольная система координат на плоскости и в пространстве

При введении системы координат на плоскости или в трехмерном пространстве появляется уникальная возможность описания геометрических фигур и их свойств при помощи уравнений и неравенств. Это имеет иное название – методы алгебры.

Данная статья поможет разобраться с заданием прямоугольной декартовой системой координат и с определением координат точек. Более наглядное и подробное изображение имеется на графических иллюстрациях.

Прямоугольная декартова система координат на плоскости

Чтобы ввести систему координат на плоскости, необходимо провести на плоскости две перпендикулярные прямые. Выбираем положительное направление, обозначая стрелочкой. Необходимо выбрать масштаб. Точку пересечения прямых назовем буквой $O$. Она считается началом отсчета. Это и называется прямоугольной системой координат на плоскости.

Прямые с началом $O$, имеющие направление и масштаб, называют координатной прямой или координатной осью.

Прямоугольная система координат обозначается $Oxy$. Координатными осями называют $Ох$ и $Оу$, называемые соответственно ось абсцисс и ось ординат.

Изображение прямоугольной системы координат на плоскости.

Оси абсцисс и ординат имеют одинаковую единицу изменения и масштаб, что показано в виде штрихе в начале координатных осей. Стандартное направление $Ох$ слева направо, а $Oy$ – снизу вверх. Иногда используется альтернативный поворот под необходимым углом.

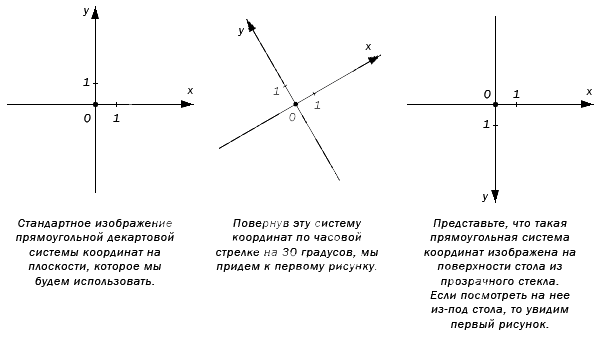
Прямоугольная система координат получила название декартовой в честь ее первооткрывателя Рене Декарта. Часто можно встретить название как прямоугольная декартовая система координат.

Прямоугольная система координат в трехмерном пространстве

Трехмерное евклидовое пространство имеет аналогичную систему, только оно состоит не из двух, а из трех $Ох$, $Оу$, $Оz$ осей. Это три взаимно перпендикулярные прямые, где $Оz$ имеет название ось аппликат.

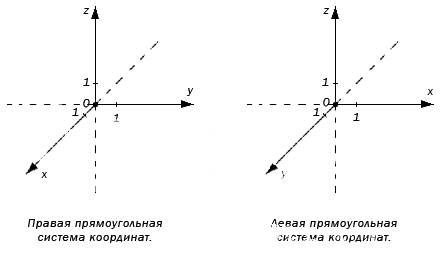
По направлению координатных осей делят на правую и левую прямоугольные системы координат трехмерного пространства.

Оси координат пересекаются в точке $O$, называемой началом. Каждая ось имеет положительное направление, которое указывается при помощи стрелок на осях. Если при повороте $Ох$ против часовой стрелки на $90°$ ее положительное направление совпадает с положительным $Оу$, тогда это применимо для положительного направления $Оz$. Такую систему считают правой. Иначе говоря, если сравнить направление $Х$ с большим пальцем руки, то указательный отвечает за $Y$, а средний за $Z$.

Аналогично образуется левая система координат. Обе системы совместить невозможно, так как соответствующие оси не совпадут.

Координаты точки в декартовой системе координат на плоскости

Для начала отложим точку $М$ на координатной оси $Ох$. Любое действительное число $x_M$ равняется единственной точке $М$, расположенной на данной прямой. Если точка расположена на координатной прямой на расстоянии $\sqrt{2}$ от начала отсчета по положительному направлению, то она равна $\sqrt{2}$ , если $-3$, то соответственное расстояние $3$. Ноль – это начало отсчета координатных прямых.

Иначе говоря, каждая точка $М$, расположенная на $Ox$, равна действительному числу $x_M$ . Этим действительным числом и является ноль, если точка $M$ расположена в начале координат, то есть на пересечении $Ox$ и $Оу$. Число длины отрезка всегда положительно, если точка удалена в положительном направлении и наоборот.

Имеющееся число $x_M$ называют координатой точки $М$ на заданной координатной прямой.

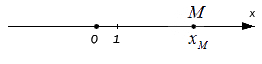
Возьмем точку как проекцию точки $M_x$ на $Ох$, а как проекцию точки $M_y$ на $Оу$. Значит, через точку $М$ можно провести перпендикулярные осям $Оx$ и $Оу$ прямые, где послучим соответственные точки пересечения  $M_x$ и $M_y$ .

Тогда точка $M_x$ на оси $Ох$ имеет соответствующее число $x_M$ , а $M_y$ на $Оу$ - $y_M$. На координатных осях это выглядит так:

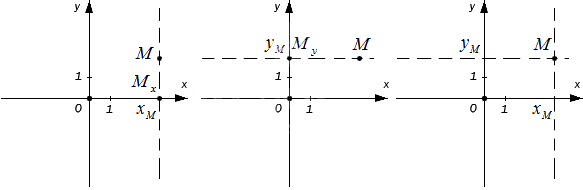
Каждая точка $M$ на заданной плоскости в прямоугольной декартовой системе координат имеет одну соответствующую пару чисел $(x_M, y_M)$, называемую ее координатами. Абсцисса $M$ – это $x_M$ , ордината $M$ – это $y_M$ .

Обратное утверждение также считается верным: каждая упорядоченная пара $(x_M, y_M)$ имеет соответствующую заданную в плоскости точку.

Координаты точки в прямоугольной системе координат в трехмерном пространстве

Определение точки $М$ в трехмерном пространстве. Пусть имеются $M_x, M_y, M_z,$ являющиеся проекциями точки $М$ на соответствующие оси $Ох, Оу, Оz$. Тогда значения этих точек на осях $Ох, Оу, Оz$ примут значения $x_M, y_M, z_M$. Изобразим это на координатных прямых.

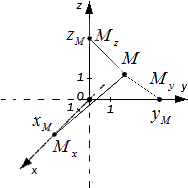
Чтобы получить проекции точки $M$, необходимо добавить перпендикулярные прямые $Ох, Оу, Оz$ продолжить и изобразит в виде плоскостей, которые проходят через $M$. Таким образом, плоскости пересекутся в $M_x, M_y, M_z$

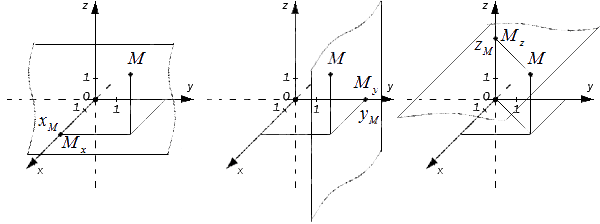
Каждая точка трехмерного пространства имеет свои данные $(x_M, y_M, z_M)$ , которые имеют название координаты точки $M$, , $x_M, y_M, z_M$- это числа, называемые абсциссой, ординатой и аппликатой заданной точки $M$. Для данного суждения верно и обратное утверждение: каждая упорядоченная тройка действительных чисел $(x_M, y_M, z_M)$ в заданной прямоугольной системе координат имеет одну соответствующую точку $M$ трехмерного пространства.