- 16 июля 2025
- 7 минут
- 8 923
Проекция вектора на ось и числовая проекция
Статью подготовили специалисты образовательного сервиса Zaochnik.
Ось – это направление. Значит, проекция на ось или на направленную прямую считается одним и тем же. Проекция бывает алгебраическая и геометрическая. В геометрическом понимают проекцию вектора на ось как вектор, а алгебраическом – число. То есть применяются понятия проекция вектора на ось и числовая проекция вектора на ось.
Если имеем ось и ненулевой вектор , то можем построить вектор , обозначив проекции его точек и .
будет являться проекцией вектора на .
Проекцией вектора на ось называют вектор, начало и конец которого являются проекции начала и конца заданного вектора. принято обозначать проекцию на . Для построения проекции на опускают перпендикуляры на .
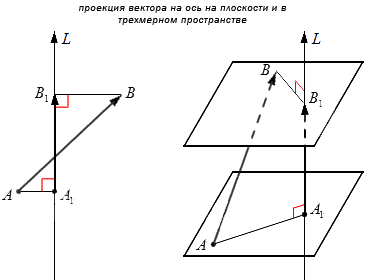
Пример проекции вектора на ось.
На координатной плоскости задается точка . Необходимо построить проекции на и для изображения радиус-вектора точки . Получим координаты векторов и .
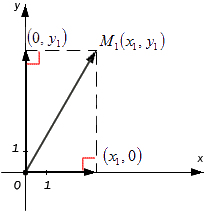
Если идет речь о проекции на ненулевой или проекции на направление , то имеется в виду проекция на ось, с которой совпадает направление . Проекция на прямую, определяемая , имеет обозначение . Известно, что когда угол между и , можно считать и сонаправленными. В случае, когда угол тупой, и противоположно направлены. В ситуации перпендикулярности и , причем - нулевой, проекция по направлению является нулевым вектором.
Числовая проекция вектора на ось
Числовая характеристика проекции вектора на ось – числовая проекция вектора на заданную ось.
Числовой проекцией вектора на ось называют число, которое равно произведению длины данного вектора на косинус угла между данным вектором и вектором, который определяет направление оси.
Числовая проекция на имеет обозначение, а на - .
Исходя из формулы, получим , откуда является длиной вектора , - угол между векторами и .
Получим формулу вычисления числовой проекции: . Она применима при известных длинах и и угле между ними. Формула применима при известных координатах и , но имеется ее упрощенный вид.
Узнать числовую проекцию на прямую по направлению при длине равной 8 и углом между ними в 60 градусов. По условию имеем . Значит, подставляем числовые значения в формулу .
Ответ: 4.
При известном , имеем как скалярное произведение и . Следуя из формулы , мы можем найти числовую проекцию направленную по вектору и получим . Формула эквивалента определению, указанному в начале пункта.
Числовой проекцией вектора на ось , совпадающей по направлению с , называют отношение скалярного произведения векторов и к длине . Формула применима для нахождения числовой проекции на прямую, совпадающую по направлению с , при известных и координатах.
Задан . Найти числовую проекцию на .
Решение
На координатной плоскости имеет вид , при и . Чтобы найти числовую проекцию вектора на ось , нужно: .
Ответ: 5.
Найти проекцию на , совпадающей с направлением , где имеются и . Задано трехмерное пространство.
Решение
По заданным и вычислим скалярное произведение: . Длину найдем по формуле . Отсюда следует, что формула определения числовой проекции будет: .
Подставляем числовые значения: .
Ответ: .
Просмотрим связь между на и длиной проекции на . Начертим ось , добавив и из точки на , после чего проведем перпендикулярную прямую с конца на и проведем проекцию на . Существуют 5 вариаций изображения:
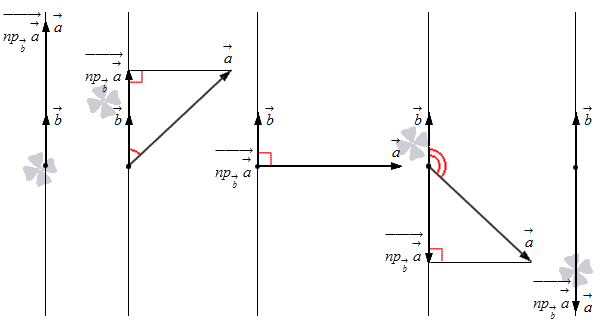
Первый случай при означает , отсюда следует .
Второй случай подразумевает применение , значит, .
Третий случай объясняет, что при получаем , тогда и .
Четвертый случай показывает , следует .
Пятый случай показывает , что означает, отсюда имеем .
Числовой проекцией вектора на ось, которая направлена как и , имеет значение:
- длины проекции вектора на при условии, если угол между и меньше 90 градусов или равен 0: с условием ;
- ноля при условии перпендикулярности и : , когда ;
- длины проекции на , умноженной на -1, когда имеется тупой или развернутый угол векторов и : с условием .
Дана длина проекции на , равная . Найти числовую проекцию при условии, что угол равен радиан.
Решение
Из условия видно, что данный угол является тупым: . Тогда можем найти числовую проекцию на : .
Ответ: .
Дана плоскость длиной вектора равной , с углом в 30 градусов. Найти координаты проекции на ось .
Решение
Для начала вычисляем числовую проекцию вектора: .
По условию угол острый, тогда числовая проекция = длине проекции вектора : . Данный случай показывает, что векторы и сонаправлены, значит имеется число, при котором верно равенство: . Отсюда видим, что , значит можем найти значение параметра : .
Тогда с координатами проекции вектора на ось равны , где необходимо умножить значения на 3. Имеем . Ответ: .
Необходимо повторить ранее изученную информацию об условии коллинеарности векторов.
Математические онлайн-калькуляторы




