Расстояние от точки до точки: формулы, примеры, решения

Содержание:

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.

Определение 1

Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.

Расстояние между точками на координатной прямой

Исходные данные: координатная прямая $O x$ и лежащая на ней произвольная точка $А$ . Любой точке прямой присуще одно действительное число: пусть для точки $А$ это будет некое число $х_{A}$ , оно же – координата точки $А$ .

Расстояние между точками на координатной прямой

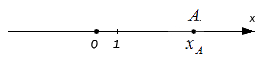
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.

Если точке $А$ соответствует целое действительное число, отложив последовательно от точки $О$ до точки по прямой $О А$ отрезки – единицы длины, мы можем определить длину отрезка $O A$ по итоговому количеству отложенных единичных отрезков.

К примеру, точке $А$ соответствует число $3$ – чтобы попасть в нее из точки $О$ , необходимо будет отложить три единичных отрезка. Если точка $А$ имеет координату $- 4$ – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние $О А$ равно $3$ ; во втором случае $О А = 4$ .

Если точка $A$ имеет в качестве координаты рациональное число, то от начала отсчета (точка $О$ ) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь $\frac{4}{111}$ .

Вышеуказанным способом отложить на прямой иррациональное число и вовсе невозможно. К примеру, когда координата точки $А$ равна $\sqrt{11}$ . В таком случае возможно обратиться к абстракции: если заданная координата точки $А$ больше нуля, то $|O A| = x_{A}$ (число принимается за расстояние); если координата меньше нуля, то $|O A| = - x_{A}$ . В общем, эти утверждения справедливы для любого действительного числа $x_{A}$ .

Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:

0, если точка совпадает с началом координат;

$x_{A}$ , если $x_{A} > 0$ ;

$- x_{A}$ , если $x_{A} < 0$ .

При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки $O$ до точки $A$ с координатой $x_{A}$ : $|O A| = |x_{A}|$

Расстояние между точками на координатной прямой

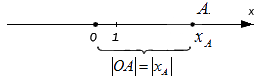
Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек $A$ и $B$ , лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты $x_{A}$ и $x_{B}$ : $|A B| = |x_{B} - x_{A}|$ .

Расстояние между точками на координатной прямой

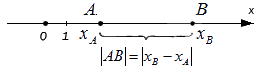
Расстояние между точками на плоскости

Исходные данные: точки $A$ и $B$ , лежащие на плоскости в прямоугольной системе координат $O x y$ с заданными координатами: $A (x_{A}, y_{A})$ и $B (x_{B}, y_{B})$ .

Проведем через точки $А$ и $B$ перпендикуляры к осям координат $O x$ и $O y$ и получим в результате точки проекции: $A_{x}$ , $A_{y}$ , $B_{x}$ , $B_{y}$ . Исходя из расположения точек $А$ и $B$ далее возможны следующие варианты:

- если точки $А$ и $В$ совпадают, то расстояние между ними равно нулю;

- если точки $А$ и $В$ лежат на прямой, перпендикулярной оси $O x$ (оси абсцисс), то точки и совпадают, а $| А В | = | А_{y} B_{y} |$ . Поскольку, расстояние между точками равно модулю разности их координат, то $|A_{y} B_{y}| = |y_{B} - y_{A}|$ , а, следовательно $|A B| = |A_{y} B_{y}| = |y_{B} - y_{A}|$ .

Расстояние между точками на плоскости

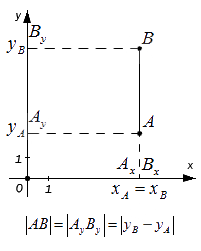
- если точки $A$ и $B$ лежат на прямой, перпендикулярной оси $O y$ (оси ординат) – по аналогии с предыдущим пунктом: $|A B| = |A_{x} B_{x}| = |x_{B} - x_{A}|$

Расстояние между точками на плоскости

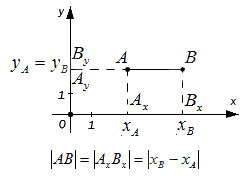
- если точки $A$ и $B$ не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:

Расстояние между точками на плоскости

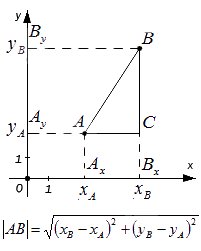
Мы видим, что треугольник $А В С$ является прямоугольным по построению. При этом $|A C| = |A_{x} B_{x}|$ и $|B C| = |A_{y} B_{y}|$ . Используя теорему Пифагора, составим равенство: ${|A B|}^{2} = {|A C|}^{2} + {|B C|}^{2} \Leftrightarrow {|A B|}^{2} = {|A_{x} B_{x}|}^{2} + {|A_{y} B_{y}|}^{2}$ , а затем преобразуем его: $|A B| = \sqrt{|A_{x} {B_{x}}^{2}| + {|A_{y} B_{y}|}^{2}} = \sqrt{{|x_{B} - x_{A}|}^{2} + {|y_{B} - y_{A}|}^{2}} = \sqrt{(x_{B} - x_{A})^{2} + (y_{B} - y_{A})^{2}}$

Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек

$|A B| = \sqrt{(x_{B} - x_{A})^{2} + (y_{B} - y_{A})^{2}}$

Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек $A$ и $B$ будет верно равенство: $|A B| = \sqrt{(x_{B} - x_{A})^{2} + (y_{B} - y_{A})^{2}} = \sqrt{0^{2} + 0^{2}} = 0$

Для ситуации, когда точки $A$ и $B$ лежат на прямой, перпендикулярной оси абсцисс:

$|A B| = \sqrt{(x_{B} - x_{A})^{2} + (y_{B} - y_{A})^{2}} = \sqrt{0^{2} + (y_{B} - y_{A})^{2}} = |y_{B} - y_{A}|$

Для случая, когда точки $A$ и $B$ лежат на прямой, перпендикулярной оси ординат:

$|A B| = \sqrt{(x_{B} - x_{A})^{2} + (y_{B} - y_{A})^{2}} = \sqrt{(x_{B} - x_{A})^{2} + 0^{2}} = |x_{B} - x_{A}|$

Расстояние между точками в пространстве

Исходные данные: прямоугольная система координат $O x y z$ с лежащими на ней произвольными точками с заданными координатами $A (x_{A}, y_{A}, z_{A})$ и $B (x_{B}, y_{B}, z_{B})$ . Необходимо определить расстояние между этими точками.

Рассмотрим общий случай, когда точки $A$ и $B$ не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки $A$ и $B$ плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: $A_{x}, A_{y}, A_{z}, B_{x}, B_{y}, B_{z}$

Расстояние между точками в пространстве

Расстояние между точками $A$ и $B$ являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: $|A_{x} B_{x}|, |A_{y} B_{y}|$ и $|A_{z} B_{z}|$

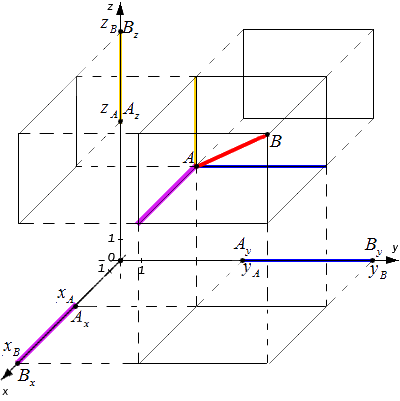
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: ${|A B|}^{2} = {|A_{x} B_{x}|}^{2} + {|A_{y} B_{y}|}^{2} + {|A_{z} B_{z}|}^{2}$

Используя полученные ранее выводы, запишем следующее:

$|A_{x} B_{x}| = |x_{B} - x_{A}|, |A_{y} B_{y}| = |y_{B} - y_{A}|, |A_{z} B_{z}| = |z_{B} - z_{A}|$

Преобразуем выражение:

${|A B|}^{2} = {|A_{x} B_{x}|}^{2} + {|A_{y} B_{y}|}^{2} + {|A_{z} B_{z}|}^{2} = {|x_{B} - x_{A}|}^{2} + {|y_{B} - y_{A}|}^{2} + {|z_{B} - z_{A}|}^{2} = = (x_{B} - x_{A})^{2} + (y_{B} - y_{A})^{2} + {(z_{B} - z_{A})}^{2}$

Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:

$|A B| = \sqrt{{(x_{B} - x_{A})}^{2} + {(y_{B} - y_{A})}^{2} + (z_{B} - z_{A})^{2}}$

Полученная формула действительна также для случаев, когда:

- точки совпадают;

- лежат на одной координатной оси или прямой, параллельной одной из координатных осей.

Примеры решения задач на нахождение расстояния между точками

Пример 1

Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами $A (1 - \sqrt{2})$ и $B (11 + \sqrt{2})$ . Необходимо найти расстояние от точки начала отсчета $O$ до точки $A$ и между точками $A$ и $B$ .

Решение

Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно $|O A| = |1 - \sqrt{2}| = \sqrt{2} - 1$
Расстояние между точками $A$ и $B$ определим как модуль разности координат этих точек: $|A B| = |11 + \sqrt{2} - (1 - \sqrt{2})| = 10 + 2 \sqrt{2}$

Ответ: $|O A| = \sqrt{2} - 1, |A B| = 10 + 2 \sqrt{2}$

Пример 2

Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней $A (1, - 1)$ и $B (λ + 1, 3)$ . $λ$ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние $А В$ будет равно $5$ .

Решение

Чтобы найти расстояние между точками $A$ и $B$ , необходимо использовать формулу $|A B| = \sqrt{(x_{B} - x_{A})^{2} + {(y_{B} - y_{A})}^{2}}$

Подставив реальные значения координат, получим: $|A B| = \sqrt{(λ + 1 - 1)^{2} + (3 - (- 1))^{2}} = \sqrt{λ^{2} + 16}$

А также используем имеющееся условие, что $|А В| = 5$ и тогда будет верным равенство:

$\sqrt{λ^{2} + 16} = 5 λ^{2} + 16 = 25 λ = \pm 3$

Ответ: $|А В| = 5$ , если $λ = \pm 3$ .

Пример 3

Исходные данные: задано трехмерное пространство в прямоугольной системе координат $O x y z$ и лежащие в нем точки $A (1, 2, 3)$ и $B (- 7, - 2, 4)$ .

Решение

Для решения задачи используем формулу $|A B| = \sqrt{{(x_{B} - x_{A})}^{2} + {(y_{B} - y_{A})}^{2} + (z_{B} - z_{A})^{2}}$

Подставив реальные значения, получим: $|A B| = \sqrt{(- 7 - 1)^{2} + (- 2 - 2)^{2} + (4 - 3)^{2}} = \sqrt{81} = 9$

Ответ: $| А В | = 9$

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.