Векторное произведение - определения, свойства, формулы, примеры и решения

Содержание:

25 сентября 2023
11 минут
3554

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Определение векторного произведения

Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов $\vec{a}, \vec{b}, \vec{c}$ в трехмерном пространстве.

Отложим для начала векторы $\vec{a}, \vec{b}, \vec{c}$ от одной точки. Ориентация тройки $\vec{a}, \vec{b}, \vec{c}$ бывает правой или левой, в зависимости от направления самого вектора $\vec{c}$ . От того, в какую сторону осуществляется кратчайший поворот от вектора $\vec{a}$ к $\vec{b}$ с конца вектора $\vec{c}$ , будет определен вид тройки $\vec{a}, \vec{b}, \vec{c}$ .

Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов $\vec{a}, \vec{b}, \vec{c}$ называется правой, если по часовой стрелке – левой.

Определение векторного произведения

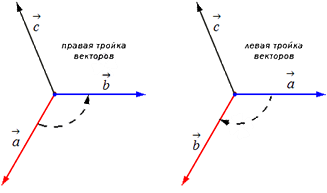
Далее возьмем два не коллинеарных вектора $\vec{a}$ и $\vec{b}$ . Отложим затем от точки $A$ векторы $\vec{A B} = \vec{a}$ и $\vec{A C} = \vec{b}$ . Построим вектор $\vec{A D} = \vec{c}$ , который одновременно перпендикулярный одновременно и $\vec{A B}$ и $\vec{A C}$ . Таким образом, при построении самого вектора $\vec{A D} = \vec{c}$ мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).

Определение векторного произведения

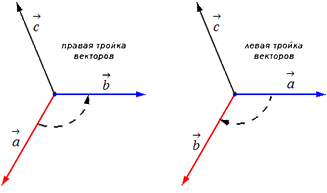
Упорядоченная тройка векторов $\vec{a}, \vec{b}, \vec{c}$ может быть, как мы выяснили правой или левой в зависимости от направления вектора.

Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.

Определение 1

Векторным произведением двух векторов $\vec{a}$ и $\vec{b}$ будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:

если векторы $\vec{a}$ и $\vec{b}$ коллинеарны, он будет нулевым;
он будет перпендикулярен и вектору $\vec{a}$ и вектору $\vec{b}$ т.е. $∠ (\vec{a} \vec{c}) = ∠ (\vec{b} \vec{c}) = \frac{π}{2}$ ;
его длина определяется по формуле: $|\vec{c}| = |\vec{a}| \cdot |\vec{b}| \cdot \sin ∠ (\vec{a}, \vec{b})$ ;
тройка векторов $\vec{a}, \vec{b}, \vec{c}$ имеет такую же ориентацию, что и заданная система координат.

Векторное произведение векторов $\vec{a}$ и $\vec{b}$ имеет следущее обозначение: $[\vec{a} \times \vec{b}]$ .

Координаты векторного произведения

Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.

Определение 2

В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов $\vec{a} = (a_{x}; a_{y}; a_{z})$ и $\vec{b} = (b_{x}; b_{y}; b_{z})$ называют вектор $\vec{c} = [\vec{a} \times \vec{b}] = (a_{y} \cdot b_{z} - a_{z} \cdot b_{y}) \cdot \vec{i} + (a_{z} \cdot b_{x} - a_{x} \cdot b_{z}) \cdot \vec{j} + (a_{x} \cdot b_{y} - a_{y} \cdot b_{x}) \cdot \vec{k}$ , где $\vec{i}, \vec{j}, \vec{k}$ являются координатными векторами.

Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты $\vec{i}, \vec{j}, \vec{k}$ , вторая строка содержит координаты вектора $\vec{a}$ , а третья – координаты вектора $\vec{b}$ в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: $\vec{c} = [\vec{a} \times \vec{b}] = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \end{matrix}|$

Разложив данный определитель по элементам первой строки, получим равенство: $\vec{c} = [\vec{a} \times \vec{b}] = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \end{matrix}| = |\begin{matrix} a_{y} & a_{z} \\ b_{y} & b_{z} \end{matrix}| \cdot \vec{i} - |\begin{matrix} a_{x} & a_{z} \\ b_{x} & b_{z} \end{matrix}| \cdot \vec{j} + |\begin{matrix} a_{x} & a_{y} \\ b_{x} & b_{y} \end{matrix}| \cdot \vec{k} =$ $= [\vec{a} \times \vec{b}] = (a_{y} \cdot b_{z} - a_{z} \cdot b_{y}) \cdot \vec{i} + (a_{z} \cdot b_{x} - a_{x} \cdot b_{z}) \cdot \vec{j} + (a_{x} \cdot b_{y} - a_{y} \cdot b_{x}) \cdot \vec{k}$

Свойства векторного произведения

Известно, что векторное произведение в координатах представляется как определитель матрицы $\vec{c} = [\vec{a} \times \vec{b}] = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \end{matrix}|$ , то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:

антикоммутативность $[\vec{a} \times \vec{b}] = - [\vec{b} \times \vec{a}]$ ;
дистрибутивность $[(\vec{a^{(1)}} + \vec{a^{(2)}}) \times b] = [\vec{a^{(1)}} \times \vec{b}] + [\vec{a^{(2)}} \times \vec{b}]$ или $[\vec{a} \times (\vec{b^{(1)}} + \vec{b^{(2)}})] = [\vec{a} \times \vec{b^{(1)}}] + [\vec{a} \times \vec{b^{(2)}}]$ ;
ассоциативность $[λ \cdot \vec{a} \times \vec{b}] = λ \cdot [\vec{a} \times \vec{b}]$ или $[\vec{a} \times (λ \cdot \vec{b})] = λ \cdot [\vec{a} \times \vec{b}]$ , где $λ$ - произвольное действительное число.

Данные свойства имеют не сложные доказательства.

Для примера можем доказать свойство антикоммутативности векторного произведения.

Доказательство антикоммутативности

По определению $[\vec{a} \times \vec{b}] = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \end{matrix}|$ и $[\vec{b} \times \vec{a}] = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ b_{x} & b_{y} & b_{z} \\ a_{x} & a_{y} & a_{z} \end{matrix}|$ . А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно, $[\vec{a} \times \vec{b}] = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \end{matrix}|$ $= - |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ b_{x} & b_{y} & b_{z} \\ a_{x} & a_{y} & a_{z} \end{matrix}| = - [\vec{b} \times \vec{a}]$ , что и доказывает антикоммутативность векторного произведения.

Векторное произведение – примеры и решения

В большинстве случаев встречаются три типа задач.

В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулой $|\vec{c}| = |\vec{a}| \cdot |\vec{b}| \cdot \sin ∠ (\vec{a}, \vec{b})$ .

Пример 1

Найдите длину векторного произведения векторов $\vec{a}$ и $\vec{b}$ , если известно $|\vec{a}| = 3, |\vec{b}| = 5, ∠ (\vec{a}, \vec{b}) = \frac{π}{4}$ .

Решение

С помощью определения длины векторного произведения векторов $\vec{a}$ и $\vec{b}$ решим данную задач: $|[\vec{a} \times \vec{b}]| = |\vec{a}| \cdot |\vec{b}| \cdot \sin ∠ (\vec{a}, \vec{b}) = 3 \cdot 5 \cdot \sin \frac{π}{4} = \frac{15 \sqrt{2}}{2}$ .

Ответ: $\frac{15 \sqrt{2}}{2}$ .

Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов $\vec{a} = (a_{x}; a_{y}; a_{z})$ и $\vec{b} = (b_{x}; b_{y}; b_{z})$ .

Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов $\vec{a}$ и $\vec{b}$ , а их разложения по координатным векторам вида $\vec{b} = b_{x} \cdot \vec{i} + b_{y} \cdot \vec{j} + b_{z} \cdot \vec{k}$ и $\vec{c} = [\vec{a} \times \vec{b}] = (a_{y} \cdot b_{z} - a_{z} \cdot b_{y}) \cdot \vec{i} + (a_{z} \cdot b_{x} - a_{x} \cdot b_{z}) \cdot \vec{j} + (a_{x} \cdot b_{y} - a_{y} \cdot b_{x}) \cdot \vec{k}$ , или векторы $\vec{a}$ и $\vec{b}$ могут быть заданы координатами точек их начала и конца.

Рассмотрим следующие примеры.

Пример 2

В прямоугольной системе координат заданы два вектора $\vec{a} = (2; 1; - 3), \vec{b} = (0; - 1; 1)$ . Найдите их векторное произведение.

Решение

По второму определению найдем векторное произведение двух векторов в заданных координатах: $[\vec{a} \times \vec{b}] = (a_{y} \cdot b_{z} - a_{z} \cdot b_{y}) \cdot \vec{i} + (a_{z} \cdot b_{x} - a_{x} \cdot b_{z}) \cdot \vec{j} + (a_{x} \cdot b_{y} - a_{y} \cdot b_{x}) \cdot \vec{k} = = (1 \cdot 1 - (- 3) \cdot (- 1)) \cdot \vec{i} + ((- 3) \cdot 0 - 2 \cdot 1) \cdot \vec{j} + (2 \cdot (- 1) - 1 \cdot 0) \cdot \vec{k} = = - 2 \vec{i} - 2 \vec{j} - 2 \vec{k} .$

Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: $[\vec{a} \times \vec{b}] = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \end{matrix}| = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ 2 & 1 & - 3 \\ 0 & - 1 & 1 \end{matrix}| =$ $- 2 \vec{i} - 2 \vec{j} - 2 \vec{k} .$

Ответ: $[\vec{a} \times \vec{b}] = - 2 \vec{i} - 2 \vec{j} - 2 \vec{k} .$

Пример 3

Найдите длину векторного произведения векторов $\vec{i} - \vec{j}$ и $\vec{i} + \vec{j} + \vec{k}$ , где $\vec{i}, \vec{j}, \vec{k}$ - орты прямоугольной декартовой системы координат.

Решение

Для начала найдем координаты заданного векторного произведения $[(\vec{i} - \vec{j}) \times (\vec{i} + \vec{j} + \vec{k})]$ в данной прямоугольной системе координат.

Известно, что векторы $\vec{i} - \vec{j}$ и $\vec{i} + \vec{j} + \vec{k}$ имеют координаты $(1; - 1; 0)$ и $(1; 1; 1)$ соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем $[(\vec{i} - \vec{j}) \times (\vec{i} + \vec{j} + \vec{k})] = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ 1 & - 1 & 0 \\ 1 & 1 & 1 \end{matrix}| = - \vec{i} - \vec{j} + 2 \vec{k} .$

Следовательно, векторное произведение $[(\vec{i} - \vec{j}) \times (\vec{i} + \vec{j} + \vec{k})]$ имеет координаты $(- 1; - 1; 2)$ в заданной системе координат.

Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): $|[(\vec{i} - \vec{j}) \times (\vec{i} + \vec{j} + \vec{k})]| = \sqrt{{(- 1)}^{2} + {(- 1)}^{2} + 2^{2}} = \sqrt{6} .$

Ответ: $|[(\vec{i} - \vec{j}) \times (\vec{i} + \vec{j} + \vec{k})]| = \sqrt{6} .$ .

Пример 4

В прямоугольной декартовой системе координат заданы координаты трех точек $A (1, 0, 1), B (0, 2, 3), C (1, 4, 2)$ . Найдите какой-нибудь вектор, перпендикулярный $\vec{A B}$ и $\vec{A C}$ одновременно.

Решение

Векторы $\vec{A B}$ и $\vec{A C}$ имеют следующие координаты $(- 1; 2; 2)$ и $(0; 4; 1)$ соответственно. Найдя векторное произведение векторов $\vec{A B}$ и $\vec{A C}$ , очевидно, что оно является перпендикулярным вектором по определению и к $\vec{A B}$ и к $\vec{A C}$ , то есть, является решением нашей задачи. Найдем его $[\vec{A B} \times \vec{A C}] = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ - 1 & 2 & 2 \\ 0 & 4 & 1 \end{matrix}| = - 6 \vec{i} + \vec{j} - 4 \vec{k} .$

Ответ: $- 6 \vec{i} + \vec{j} - 4 \vec{k} .$ - один из перпендикулярных векторов.

Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.

Пример 5

Векторы $\vec{a}$ и $\vec{b}$ перпендикулярны и их длины равны соответственно $3$ и $4$ . Найдите длину векторного произведения $[(3 \cdot \vec{a} - \vec{b}) \times (\vec{a} - 2 \cdot \vec{b})] = [(3 \cdot \vec{a}) \times (\vec{a} - 2 \cdot \vec{b})] + [(- \vec{b}) \times (\vec{a} - 2 \cdot \vec{b})] = = [(3 \cdot \vec{a}) \times \vec{a}] + [(3 \cdot \vec{a}) \times (- 2 \cdot \vec{b})] + [(- \vec{b}) \times \vec{a}] + [(- \vec{b}) \times (- 2 \cdot \vec{b})]$ .

Решение

По свойству дистрибутивности векторного произведения мы можем записать $[(3 \cdot \vec{a} - \vec{b}) \times (\vec{a} - 2 \cdot \vec{b})] = [(3 \cdot \vec{a}) \times (\vec{a} - 2 \cdot \vec{b})] + [(- \vec{b}) \times (\vec{a} - 2 \cdot \vec{b})] = = [(3 \cdot \vec{a}) \times \vec{a}] + [(3 \cdot \vec{a}) \times (- 2 \cdot \vec{b})] + [(- \vec{b}) \times \vec{a}] + [(- \vec{b}) \times (- 2 \cdot \vec{b})]$

По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: $[(3 \cdot \vec{a}) \times \vec{a}] + [(3 \cdot \vec{a}) \times (- 2 \cdot \vec{b})] + [(- \vec{b}) \times \vec{a}] + [(- \vec{b}) \times (- 2 \cdot \vec{b})] = = 3 \cdot [\vec{a} \times \vec{a}] + 3 \cdot (- 2) \cdot [\vec{a} \times \vec{b}] + (- 1) \cdot [\vec{b} \times \vec{a}] + (- 1) \cdot (- 2) \cdot [\vec{b} \times \vec{b}] = = 3 \cdot [\vec{a} \times \vec{a}] - 6 \cdot [\vec{a} \times \vec{b}] - [\vec{b} \times \vec{a}] + 2 \cdot [\vec{b} \times \vec{b}]$

Векторные произведения $[\vec{a} \times \vec{a}]$ и $[\vec{b} \times \vec{b}]$ равны 0, так как $[\vec{a} \times \vec{a}] = |\vec{a}| \cdot |\vec{a}| \cdot \sin 0 = 0$ и $[\vec{b} \times \vec{b}] = |\vec{b}| \cdot |\vec{b}| \cdot \sin 0 = 0$ , тогда $3 \cdot [\vec{a} \times \vec{a}] - 6 \cdot [\vec{a} \times \vec{b}] - [\vec{b} \times \vec{a}] + 2 \cdot [\vec{b} \times \vec{b}] = - 6 \cdot [\vec{a} \times \vec{b}] - [\vec{b} \times \vec{a}] .$ .

Из антикоммутативности векторного произведения следует $- 6 \cdot [\vec{a} \times \vec{b}] - [\vec{b} \times \vec{a}] = - 6 \cdot [\vec{a} \times \vec{b}] - (- 1) \cdot [\vec{a} \times \vec{b}] = - 5 \cdot [\vec{a} \times \vec{b}] .$ .

Воспользовавшись свойствами векторного произведения, получаем равенство $[(3 \cdot \vec{a} - \vec{b}) \times (\vec{a} - 2 \cdot \vec{b})] =$ $= - 5 \cdot [\vec{a} \times \vec{b}] .$

По условию векторы $\vec{a}$ и $\vec{b}$ перпендикулярны, то есть угол между ними равен $\frac{π}{2}$ . Теперь остается лишь подставить найденные значения в соответствующие формулы: $|[(3 \cdot \vec{a} - \vec{b}) \times (\vec{a} - 2 \cdot \vec{b})]| =$ $|- 5 \cdot [\vec{a} \times \vec{b}]| =$ $= 5 \cdot |[\vec{a} \times \vec{b}]| = 5 \cdot |\vec{a}| \cdot |\vec{b}| \cdot \sin (\vec{a}, \vec{b}) = 5 \cdot 3 \cdot 4 \cdot \sin \frac{π}{2} = 60 .$

Ответ: $[(3 \cdot \vec{a} - \vec{b}) \times (\vec{a} - 2 \cdot \vec{b})] = 60 .$

Геометрический смысл векторного произведения

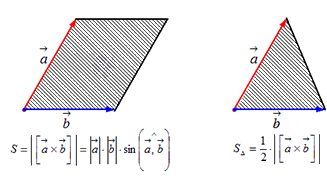
Длина векторного произведения векторов по орпеделению равна $|[\vec{a} \times \vec{b}]| = |\vec{a}| \cdot |\vec{b}| \cdot \sin ∠ (\vec{a}, \vec{b})$ . Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма - удвоенного треугольника, а именно произведению сторон в виде векторов $\vec{a}$ и $\vec{b}$ , отложенные от одной точки, на синус угла между ними $\sin ∠ (\vec{a}, \vec{b})$ .

Это и есть геометрический смысл векторного произведения.

Геометрический смысл векторного произведения

Физический смысл векторного произведения

В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.

Определение 3

Под моментом силы $\vec{F}$ , приложенной к точке $B$ , относительно точки $A$ будем понимать следующее векторное произведение $[\vec{A B} \times \vec{F}]$ .

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.