Разложение дроби на простейшие

Произвести разложение дроби вида $\frac{-2x+3}{x^3+x}$.

Решение

Когда степень числителя многочлена меньше степени многочлена в знаменателе, имеет место разложение на простейшие дроби. Иначе применяется деление для выделения целой части, после чего производят разложение дробно-рациональной функции.

Применим деление углом. Получаем, что

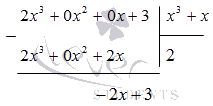
Отсюда следует, что дробь примет вид

$\frac{2x^3+3}{x^3+x}=2+\frac{-2x+3}{x^3+x}$

Значит, такое разложение приведет к тому, что результат будет равен $\frac{-2x+3}{x^3+x}$.

Когда в знаменателе имеется  выражение вида $(x-a)(x-b)(x-c)(x-d)$, количество множителей не имеет значения, дробь можно представить в виде дроби первого типа $\frac{A}{x-a}+\frac{B}{x-b}+\frac{C}{x-c}+\frac{D}{x-d}$, где $a$, $b$, $c$ и $d$ являются числами, $A$, $B$, $C$ и $D$ – неопределенными коэффициентами.

Когда знаменатель имеет выражение $(x-a{)}^2(x-b{)}^4(x-c{)}^3$, количество множителей также не имеет значения, причем саму дробь необходимо привести ко второму или первому типу вида:

$$\begin{gathered} \frac{A_2}{{\left(x-a\right)}^2}+\frac{{\displaystyle A_1}}{{\displaystyle x-a}}+\frac{{\displaystyle B_4}}{{\displaystyle {\left(x-b\right)}^4}}+\frac{{\displaystyle B_3}}{{\displaystyle {\left(x-b\right)}^3}}+\frac{{\displaystyle B_2}}{{\displaystyle {\left(x-b\right)}^2}}+\frac{{\displaystyle B_1}}{{\displaystyle x-b}}+ \\ +\frac{{\displaystyle C_3}}{{\displaystyle {\left(x-c\right)}^3}}+\frac{{\displaystyle C_2}}{{\displaystyle {\left(x-c\right)}^2}}+\frac{{\displaystyle C_1}}{{\displaystyle x-c}} \end{gathered}$$

где имеющиеся $a$, $b$, $c$ являются числами, а $A_1, A_2, B_1, B_2, B_3, B_4, C_1, C_2, C_3$ - неопределенными коэффициентами. Какова степень многочлена, такое количество слагаемых имеем.

Когда знаменатель имеет вид типа $\left(x^2+px+q\right)\left(x^2+rx+s\right)$, тогда количество квадратичных функций значения не имеет,  а дробь принимает вид третьего типа $\frac{Px+Q}{x^2+px+q}+\frac{Rx+S}{x^2+rx+s}$,где имеющиеся $p$, $q$, $r$ и $s$ являются числами, а $P$, $Q$, $R$ и $S$ – определенными коэффициентами.

Когда знаменатель имеет вид ${\left(x^2+px+q\right)}^4{\left(x^2+rx+s\right)}^2$, количество множителей значения не имеет также , как и их степени, дробь представляется в виде третьего и четверного типов вида

$$\begin{gathered} \frac{P_{4}x+Q_4}{(x^2+px+q{)}^4}+\frac{{\displaystyle P_{3}x+Q_3}}{{\displaystyle (x^2+px+q{)}^3}}+\frac{{\displaystyle P_{2}x+Q_2}}{{\displaystyle (x^2+px+q{)}^2}}+\frac{{\displaystyle P_{1}x+Q_1}}{{\displaystyle x^2+px+q}}+ \\ +\frac{{\displaystyle R_{2}x+S_2}}{{\displaystyle (x^2+rx+s{)}^2}}+\frac{{\displaystyle R_{1}x+S_1}}{{\displaystyle x^2+rx+s}} \end{gathered}$$

где имеющиеся $p$, $q$, $r$ и $s$ являются числами, а $P_1,P_2,P_3,P_4,R_1,R_2,S_1,S_2$ - неопределенными коэффициентами.

Когда имеется знаменатель вида $(x-a)(x-b{)}^3(x^2+px+q\left)\right(x^2+rx+s{)}^2$, тогда дробь необходимо представить в виде четвертого типа

$$\begin{gathered} \frac{A}{x-a}+\frac{{\displaystyle B_3}}{{\displaystyle {\left(x-b\right)}^3}}+\frac{{\displaystyle {В}_2}}{{\displaystyle {\left(x-b\right)}^2}}+\frac{{\displaystyle {В}_1}}{{\displaystyle x-b}}+ \\ +\frac{{\displaystyle Px+Q}}{x^2+px+q}+\frac{{\displaystyle R_{2}x+S_2}}{{\displaystyle {\left(x^2+rx+s\right)}^2}}+\frac{{\displaystyle R_{1}x+S_1}}{x^2+rx+s} \end{gathered}$$

Произвести разложение дроби $\frac{2x^2-x-7}{x^3-5x^2+6x}$.

Решение

По условию имеем, что степень многочлена числителя меньше степени многочлена знаменателя, тогда деление выполнять не нужно. Необходимо перейти  к разложению на множители. для начала необходимо выполнить вынесение х за скобки. Получим, что

$x^3-5x^2+6x=x(x^2-5x+6)$

Квадратный трехчлен $x^2-5x+6$ имеет корни, которые находим не по дискриминанту, а по теореме Виета. Получим:

$\left\{\begin{array}{l}{x}_1+x_2=5\\ x_1·x_2=6\end{array}\right.\iff \left\{\begin{array}{l}{x}_1=3\\ x_2=2\end{array}\right.$

Запись трехчлена может быть в виде $x^2-5x+6=(x-3)(x-2)$.

Тогда изменится знаменатель:$x^2-5x^2+6x=x(x^2-5x+6)=x(x-3)(x-2)$

Имея такой знаменатель, дробь раскладываем на простейшие дроби с неопределенными коэффициентами. Выражение примет вид:

$\frac{2x^2-x-7}{x^3-5x^2+6x}=\frac{2x^2-x-7}{x(x-3)(x-2)}=\frac{A}{x}+\frac{B}{x-3}+\frac{C}{x-2}$

Полученный результат необходимо приводить к общему знаменателю. Тогда получаем:

$$\begin{gathered} \frac{2x^2-x-7}{x^3-5x^2+6x}=\frac{2x^2-x-7}{x(x-3)(x-2)}=\frac{A}{x}+\frac{B}{x-3}+\frac{C}{x-2}= \\ =\frac{A(x-3)(x-2)+Bx(x-2)+Cx(x-3)}{x(x-3)(x-2)} \end{gathered}$$

После упрощения придем к неравенству вида

$$\begin{gathered} \frac{2x^2-x-7}{x(x-3)(x-2)}=\frac{A(x-3)(x-2)+Bx(x-2)+Cx(x-3)}{x(x-3)(x-2)}\Rightarrow \\ \Rightarrow 2x^2-x-7=A(x-3)(x-2)+Bx(x-2)+Cx(x-3) \end{gathered}$$

Теперь переходим к нахождению неопределенных коэффициентов. Нужно подставлять полученные значения в равенство для того, чтобы знаменатель обратился в ноль, то есть значения $х=0$, $х=2$ и $х=3$.

Если $х=0$, получим:

$$\begin{gathered} 2·0^2-0-7=A(0-3)(0-2)+B·0·(0-2)+C·0·(0-3) \\ -7=6A\Rightarrow \\ A=-\frac{7}{6} \end{gathered}$$

Если $x=2$, тогда

$$\begin{gathered} 2·2^2-2-7=A(2-3)(2-2)+B·2·(2-2)+C·2·(2-3) \\ -1=-2C\Rightarrow \\ C=\frac{1}{2} \end{gathered}$$

Если $x=3$, тогда

$$\begin{gathered} 2·3^2-3-7=A(3-3)(3-2)+B·3·(3-2)+C·3·(3-3) \\ 8=3B\Rightarrow \\ B=\frac{8}{3} \end{gathered}$$

Ответ: $\frac{2x^2-x-7}{x^3-5x^2+6x}=\frac{A}{x}+\frac{B}{x-3}+\frac{C}{x-2}=-\frac{7}{6}·\frac{1}{x}+\frac{8}{3}·\frac{1}{x-3}+\frac{1}{2}·\frac{1}{x-2}$

Произвести разложение выражения $\frac{x^4+3x^3+2x-11}{(x-1)(x+1)(x-3{)}^3}$ на простейшие дроби.

Решение

По условию имеем, что степень числителя многочлена меньше знаменателя, значит зазложение примет вид

$\frac{x^4+3x^3+2x-11}{(x-1)(x+1)(x-3{)}^3}=\frac{A}{x-1}+\frac{B}{x+1}+\frac{C}{(x-3{)}^3}+\frac{C}{(x-3{)}^2}+\frac{C}{x-3}$

Производим приведение к общему знаменателю. Имеем, что

$$\begin{gathered} \frac{x^4+3x^3+2x-11}{(x-1)(x+1)(x-3{)}^3}=\frac{A}{x-1}+\frac{B}{x+1}+\frac{C}{(x-3{)}^3}+\frac{C}{(x-3{)}^2}+\frac{C}{x-3}= \\ =\left(\begin{array}{c}\begin{array}{c}\frac{A(x+1)(x-3{)}^3+B(x-1\left)\right(x-3{)}^3}{(x-1)(x+1)(x-3{)}^3}\end{array}+\\ +\frac{C_3(x-1)(x+1)+C_2(x-1)(x+1)(x-3)+C_1(x-1)(x+1)(x-3{)}^2}{(x-1)(x+1)(x-3{)}^3}\end{array}\right) \end{gathered}$$

Приравняем числители и получим, что

$$\begin{gathered} x^4+3x^3+2x+11= \\ =A(x+1)(x-3{)}^3+B(x-1\left)\right(x-3{)}^3+ \\ +C_3(x-1)(x+1)+C_2(x-1)(x+1)(x-3)+C_1(x-1)(x+1)(x-3{)}^2 \end{gathered}$$

Из выше написанного понятно, что нули знаменателя – это $х=1$,$х=-1$ и$х=3$. Тогда применим метод частных решений. Для этого подставим значения х. получим, что если х=1:

$-5=-16A\Rightarrow A=\frac{5}{16}$

Если $х=-1$

$-15=128B\Rightarrow B=-\frac{15}{128}$

Если $х=3$

$157=8C_3\Rightarrow C_3=\frac{157}{8}$

Отсюда следует, что нужно найти значения $C_1$ и $C_3$.

Поэтому подставим полученный значения  в числитель, тогда

$$\begin{gathered} x^4+3x^3+2x-11= \\ =\frac{5}{16}(x+1)(x-3{)}^3-\frac{15}{128}(x-1\left)\right(x-3{)}^3+\frac{157}{8}(x-1)(x+1)+ \\ +C_2(x-1)(x+1)(x-3)+C_1(x-1)(x+1)(x-3{)}^2 \end{gathered}$$

Раскроем скобки для того, чтобы привести подобные слагаемые с одинаковыми степенями. Придем к выражению вида

$$\begin{gathered} x^4+3x^3+2x-11=x^4\left(\frac{25}{128}+C_1\right)+x^3\left(-\frac{85}{64}+C_2-6C_1\right)+ \\ +x^2\left(\frac{673}{32}-3C_2+8C_1\right)+x\left(\frac{405}{64}-C_2+6C_1\right)+3C_2-9C_1-\frac{3997}{128} \end{gathered}$$

Необходимо приравнять соответствующие коэффициенты с одинаковыми степенями, тогда сможем найти искомое значение $C_1$ и $C_3$.  Теперь необходимо решить систему:

$\left\{\begin{array}{l}\begin{array}{c}\frac{25}{128}+C_1=1\\ -\frac{85}{64}+C_2-6C_1=3\\ \frac{673}{32}-3C_2+8C_1=0\end{array}\\ \begin{array}{c}\frac{405}{64}-C_2+6C_1=2\\ 3C_2-9C_1-\frac{3997}{128}=11\end{array}\end{array}\right.$

Первое уравнение дает возможность найти $C_1=\frac{103}{128}$, а второе $C_2=3+\frac{85}{64}+6C_1=3+\frac{85}{64}+6·\frac{103}{128}=\frac{293}{32}$.

Итог решения – это искомое разложение дроби на простейшие вида:

$$\begin{gathered} \frac{x^4+3x^3+2x-11}{(x-1)(x+1)(x-3{)}^3}=\frac{A}{x-1}+\frac{B}{x+1}+\frac{C_3}{{\displaystyle {\left(x-3\right)}^3}}+\frac{C_2}{{\left(x-3\right)}^2}+\frac{C_1}{x-3}= \\ =\frac{5}{16}\frac{1}{x-1}-\frac{15}{128}\frac{1}{x+1}+\frac{157}{8}·\frac{1}{{\left(x-3\right)}^3}+\frac{293}{32}\frac{1}{{\displaystyle {\left(x-3\right)}^2}}+\frac{103}{128}\frac{1}{x-3} \end{gathered}$$

Примечание

При непосредственном применении метода неопределенных коэффициентов необходимо было бы решать все пять линейных уравнений, объединенных в систему. Такой метод упрощает поиск значения переменных и дальнейшее решение в совокупности. Иногда применяется несколько методов. Это необходимо для быстрого упрощения всего выражения и поиска результата.