- 16 июля 2025
- 15 минут
- 9 800
Разложение многочлена на множители
Статью подготовили специалисты образовательного сервиса Zaochnik.
Для того, чтобы разложить на множители, необходимо упрощать выражения. Это необходимо для того, чтобы можно было в дальнейшем сократить. Разложение многочлена имеет смысл тогда, когда его степень не ниже второй. Многочлен с первой степенью называют линейным.
Статья раскроет все понятия разложения, теоретические основы и способы разложений многочлена на множители.
Теория
Когда любой многочлен со степенью , имеющие вид , представляют в виде произведения с постоянным множителем со старшей степенью и линейных множителей , , тогда , где , – это и есть корни многочлена.
Теорема предназначена для корней комплексного типа , и для комплексных коэффициентов ,. Это и есть основа любого разложения.
Когда коэффициенты вида , являются действительными числами, тогда комплексные корни, которые будут встречаться сопряженными парами. Например, корни и , относящиеся к многочлену вида считаются комплексно сопряженным, тогда другие корни являются действительными, отсюда получаем, что многочлен примет вид , где .
Замечание
Корни многочлена могут повторяться. Рассмотрим доказательство теоремы алгебры, следствия из теоремы Безу.
Основная теорема алгебры
Любой многочлен со степенью имеет как минимум один корень.
Теорема Безу
После того, как произвели деление многочлена вида на , тогда получаем остаток, который равен многочлену в точке , тогда получим
, где является многочленом со степенью .
Следствие из теоремы Безу
Когда корень многочлена считается , тогда . Данное следствие является достаточным при употреблении для описания решения.
Разложение на множители квадратного трехчлена
Квадратный трехчлен вида можно разложить на линейные множители. тогда получим, что , где и - это корни (комплексные или действительные).
Отсюда видно, что само разложение сводится к решению квадратного уравнения впоследствии.
Произвести разложение квадратного трехчлена на множители.
Решение
Необходимо найти корни уравнения . Для этого необходимо найти значение дискриминанта по формуле, тогда получим . Отсюда имеем, что
Отсюда получаем, что .
Для выполнения проверки нужно раскрыть скобки. Тогда получим выражение вида:
После проверки приходим к исходному выражению. То есть можно сделать вывод, что разложение выполнено верно.
Произвести разложение на множители квадратный трехчлен вида .
Решение
Получим, что необходимо вычислить получившееся квадратное уравнение вида .
Чтобы найти корни, надо определить значение дискриминанта. Получим, что
Отсюда получаем, что .
Произвести разложение многочлена на множители.
Решение
Теперь нужно решить квадратное уравнение и найти его корни. Получим, что
Эти корни называют комплексно сопряженными, значит само разложение можно изобразить как .
Произвести разложение квадратного трехчлена .
Решение
Для начала необходимо решить квадратное уравнение вида и найти его корни.
Получив корни, запишем
Замечание
Если значение дискриминанта отрицательное, то многочлены останутся многочленами второго порядка. Отсюда следует, что раскладывать их не будем на линейные множители.
Способы разложения на множители многочлена степени выше второй
При разложении предполагается универсальный метод. Большинство всех случаев основано на следствии из теоремы Безу. Для этого необходимо подбирать значение корня и понизить его степень при помощи деления на многочлена на делением на . Полученный многочлен нуждается в нахождении корня , причем процесс поиска цикличен до тех пор, пока не получим полное разложение.
Если корень не нашли, тогда применяются другие способы разложения на множители: группировка, дополнительные слагаемые. Данная тема полагает решение уравнений с высшими степенями и целыми коэффициентами.
Вынесение общего множителя за скобки
Рассмотрим случай, когда свободный член равняется нулю, тогда вид многочлена становится как .
Видно, что корень такого многочлена будет равняться , тогда можно представить многочлен в виде выражения
Данный способ считается вынесением общего множителя за скобки.
Выполнить разложение многочлена третьей степени на множители.
Решение
Видим, что - это корень заданного многочлена, тогда можно произвести вынесение х за скобки всего выражения. Получаем:
Переходим к нахождению корней квадратного трехчлена . Найдем дискриминант и корни:
Тогда следует, что
Разложение на множители многочлена с рациональными корнями
Для начала примем за рассмотрение способ разложения, содержащий целые коэффициенты вида , где коэффициента при старшей степени равняется .
Когда многочлен имеет целые корни, тогда их считают делителями свободного члена.
Произвести разложение выражения .
Решение
Рассмотрим, имеются ли целые корни. Необходимо выписать делители числа . Получим, что . Отсюда следует, что данный многочлен имеет целые корни. Можно провести проверку по схеме Горнера. Она очень удобная и позволяет быстро получить коэффициенты разложения многочлена:
| Коэффициенты многочленов | |||||
Отсюда следует, что и – это корни исходного многочлена, который можно представить как произведение вида:
Переходим к разложению квадратного трехчлена вида .
Так как дискриминант получаем отрицательный, значит, действительных корней нет.
Ответ:
Замечание
Допускается использование подбором корня и деление многочлена на многочлен вместо схемы Горнера. Перейдем к рассмотрению разложения многочлена, содержащим целые коэффициенты вида , старший из которых на равняется единице.
Этот случай имеет место быть для дробно-рациональных дробей.
Произвести разложение на множители .
Решение
Необходимо выполнить замену переменной , следует переходить к многочлену с коэффициентами равными при старшей степени. Необходимо начать с умножения выражения на . Получаем, что
Когда получившаяся функция вида имеет целые корни, тогда их нахождение среди делителей свободного члена. Запись примет вид:
Перейдем к вычислению функции в этих точка для того, чтобы получить в результате ноль. Получаем, что
Получаем, что – это корень уравнения вида , значит, - это корень исходной функции.
Необходимо произвести деление столбиком на .
Решение
Запишем и получим:
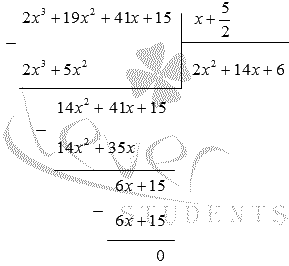
Значит,
Проверка делителей займет много времени, поэтому выгодней предпринять разложение на множители полученного квадратного трехчлена вида . Приравниванием к нулю и находим дискриминант.
Отсюда следует, что
Искусственные приемы при разложении многочлена на множители
Рациональные корни не присущи всем многочленам. Для этого необходимо пользоваться специальными способами для нахождения множителей. Но не все многочлены можно разложить или представить в виде произведения.
Способ группировки
Бывают случаи, когда можно сгруппировывать слагаемые многочлена для нахождения общего множителя и вынесения его за скобки.
Произвести разложение многочлена на множители.
Решение
Потому как коэффициенты – целые числа, тогда корни предположительно тоже могут быть целыми. Для проверки возьмем значения , , и для того, чтобы вычислить значение многочлена в этих точках. Получаем, что
Отсюда видно, что корней нет, необходимо использовать другой способ разложения и решения.
Необходимо провести группировку:
После группировки исходного многочлена необходимо представить его как произведение двух квадратных трехчленов. Для этого нам понадобится произвести разложение на множители. получаем, что
Значит:
Замечание
Простота группировки не говорит о том, что выбрать слагаемы достаточно легко. Определенного способа решения не существует, поэтому необходимо пользоваться специальными теоремами и правилами.
Произвести разложение на множители многочлен .
Решение
Заданный многочлен не имеет целых корней. Следует произвести группировку слагаемых. Получаем, что
После разложения на множители получим, что
Использование формул сокращенного умножения и бинома Ньютона для разложения многочлена на множители
Внешний вид зачастую не всегда дает понять, каким способом необходимо воспользоваться при разложении. После того, как были произведены преобразования, можно выстроить строчку, состоящую из треугольника Паскаля, иначе их называют биномом Ньютона.
Произвести разложение многочлена на множители.
Решение
Необходимо выполнить преобразование выражения к виду
На последовательность коэффициентов суммы в скобках указывает выражение .
Значит, имеем .
После применения разности квадратов, получим
Рассмотрим выражение, которое находится во второй скобке. Понятно, что там коней нет, поэтому следует применить формулу разности квадратов еще раз. Получаем выражение вида
Произвести разложение на множители .
Решение
Займемся преобразованием выражения. Получаем, что
Необходимо применить формулу сокращенного умножения разности кубов. Получаем:
Способ замены переменной при разложении многочлена на множители
При замене переменной производится понижение степени и разложение многочлена на множители.
Произвести разложение на множители многочлена вида .
Решение
По условию видно, что необходимо произвести замену . Получаем:
Корни полученного квадратного уравнения равны и , тогда
Необходимо применить формулу сокращенного умножения суммы кубов. Получим выражения вида:
То есть получили искомое разложение.
Рассмотренные выше случаи помогут в рассмотрении и разложении многочлена на множители разными способами.
Математические онлайн-калькуляторы




