Действия с рациональными числами: правила, примеры, решения

Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.

Действие сложения рациональных чисел

Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как $5+\frac{1 }{4}$возможно описать следующим образом: к $5$ целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.

Сформулируем правила сложения рациональных чисел:

Сложение нуля с отличным от него рациональным числом

Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства:$a + 0 = a$ (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: $0 + a = a$.

Пара простых примеров: сумма рационального числа $2,1$ и числа $0$ равно $2,1$ и: $6\frac{4}{5}+0 = 6\frac{4}{5}$.

Сложение противоположных рациональных чисел

Сумма противоположных чисел равна нулю.

Данное правило можно записать в виде: $a+(-a)=0$ (для любого рационального числа $a$).

К примеру, числа $45,13$ и $-45,13$ являются противоположными, т.е. их сумма равно нулю: $45,13+(-45,13) = 0$.

Сложение положительных рациональных чисел

В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.

Необходимо произвести сложение рациональных чисел: $0,6$ и $\frac{5}{9}$.

Решение

Выполним перевод десятичной дроби в обыкновенную и тогда: $0,6 + \frac{5}{9} = \frac{6}{10} + \frac{5}{9}$.

Осуществим сложение дробей с разными знаменателями:

$\frac{6}{10}+\frac{5}{9}= \frac{54}{90}+ \frac{50}{90}= \frac{104}{90}=1\frac{7}{45}$

Ответ: $0,6 + \frac{5}{9}= 1\frac{7}{45}$.

Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.

Сложение рациональных чисел с разными знаками

Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.

Необходимо осуществить сложение рациональных чисел с разными знаками $8,2$ и $-2\frac{3}{4}$ .

Решение

Согласно исходным данным, необходимо произвести сложение положительного числа с отрицательным. Придерживаясь вышеуказанного правила, определим модули заданных чисел: $|8,2| = 8,2$ и$|-2\frac{3}{4}|=2\frac{3}{4}$. Проведя сравнение модулей - рациональных чисел, получим: $8,2 > 2\frac{3}{4}$ и соответственно поймем, какое число из заданных станет уменьшаемым, а какое - вычитаемым. Произведем вычитание смешанных чисел, т.е.:$8,2-2\frac{3}{4}= 8\frac{2}{10}- 2\frac{3}{4}= 5\frac{9 }{20}$.

Полученному результату присваивается знак плюс, т.к. бОльшее из слагаемых по модулю – положительное число. Ответ: $8,2 +(-2\frac{3}{4})= 5\frac{9}{20}$.

Сложение отрицательных рациональных чисел

Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.

Необходимо произвести сложение чисел: $-4,0203$ и $-12,193$.

Решение

Модули заданных чисел соответственно равны: $4,0203$ и $12,193$. Сложим их:

​​​​​​

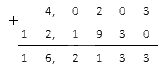
Полученному результату присваиваем знак минус: $-16,2133$.

Ответ: $(-4,0203)+(-12,193) =-16,2133$.

Действие вычитания рациональных чисел

Вычитание – действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства $c+b=a$ следует, что$a-b=c$и $a-c=b$. И наоборот: из равенств $a-b =c$ и $a-c=b$следует, что $c+b=a$.

При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.

Необходимо вычислить разность рациональных чисел: $4,\left(36\right)– \frac{1}{5}$.

Решение

Сначала переведем периодическую десятичную дробь в обыкновенную: $4,\left(36\right) = 4+(0,36 + 0,0036 +\dots )= 4+\frac{0,36}{1-0,01}=4 + \frac{36}{99}=4+ \frac{4}{11}= 4\frac{4}{11}$

Далее переходим к действию вычитания обыкновенной дроби из смешанного числа: $4, \left(36\right)-\frac{1}{5}= 4\frac{4}{11}- \frac{1}{5}=4 + \frac{4}{11}-\frac{1}{5}=4+\left(\frac{20}{55}- \frac{11}{55}\right)=4+\frac{9}{55}=4\frac{9}{55}$

Ответ: $4,\left(36\right)-\frac{1}{5}= 4\frac{9}{55}$

В прочих случаях вычитание рациональных чисел необходимо заменить сложением: к уменьшаемому прибавить число, противоположное вычитаемому:$a–b=a+(-b)$.

Указанное равенство можно доказать, опираясь на свойства действий с рациональными числами. Они дают возможность записать цепочку равенств: $(a+(-b\left)\right)+b=a+\left(\right(-b)+b)=a+0=a$. Отсюда в силу смысла действия вычитания следует, что сумма $a+(-b)$ есть разность чисел $a$ и $b$.

Необходимо из рационального числа $\frac{2}{7}$ вычесть рациональное число $5\frac{3}{7}$

Решение

Согласно последнему указанному правилу используем для дальнейших действий число, противоположное вычитаемому, т.е. $-5\frac{3}{7}$. Тогда: $\frac{2}{7}-5\frac{3}{7}=\frac{2}{7}+\left(-5\frac{3}{7}\right)$

Далее произведем сложение рациональных чисел с разными знаками: $\frac{2}{7}+-5\frac{3}{7}=-5\frac{3}{7}-\frac{2}{7}=-5\frac{3}{7}-\frac{2}{7}= -5\frac{1}{7}$

Ответ:$\frac{2}{7}+-5\frac{3}{7}=-5\frac{1}{7}$

Действие умножения рациональных чисел

Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.

Умножение на нуль

Произведение любого рационального числа $a$ на нуль есть нуль.

Т.е. $a·0=0$.

Используя переместительное свойство умножения, получим: $0·а=0$.

К примеру, умножение рационального числа $\frac{7}{13}$ на $0$ даст$0$. Перемножив отрицательное рациональное число $-7\frac{1}{8}$и нуль, также получим нуль. В частном случае, произведение нуля на нуль есть нуль: $0·0=0$.

Умножение на единицу

Умножение любого рационального числа $a$ на $1$ дает число $a$.

Т.е. $a·1=a$ или $1 · a = a$ (для любого рационального $a$). Единица здесь является нейтральным числом по умножению.

К примеру, умножение рационального числа $5,46$ на $1$ даст в итоге число $5,46$.

Умножение взаимообратных чисел

Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : $а·{а}^{-1}=1$.

К примеру, результатом произведения чисел $\frac{5}{6}$ и $\frac{6}{5}$ будет единица.

Умножение положительных рациональных чисел

В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.

Необходимо вычислить произведение положительных рациональных чисел $0,5$ и $\frac{6}{25}$.

Решение

Представим заданную десятичную дробь в виде обыкновенной $0,5 = \frac{5}{10}= \frac{1}{2}$.

Далее произведем умножение обыкновенных дробей: $\frac{1}{2} · \frac{6}{25}= \frac{6}{50}= \frac{3}{25}$.

Ответ:$0,5 ·\frac{6}{25}= \frac{3}{25}$

Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.

Необходимо вычислить произведение рациональных чисел $2,121$ и $3,4$.

Решение

Перемножим десятичные дроби столбиком:

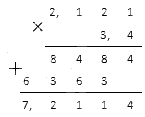
Ответ: $2,121 · 3,4 = 7,2114$

В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.

Умножение рациональных чисел с разными знаками

Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.

Необходимо найти произведение чисел: $-3\frac{3}{8}$и $2\frac{1}{2}$

Решение

Согласно вышеуказанному правилу получим: $\left(-3\frac{3}{8}\right)·2\frac{1}{2}=\left(\left.open-3\frac{3}{8}\right|·\left.open2\frac{1}{2}\right|\right)=-\left(3\frac{3}{8}·2\frac{1}{2}\right)$

Заменим смешанные дроби неправильными и найдем искомое произведение: $-\left(3\frac{3}{8}·2\frac{1}{2}\right)=-\left(\frac{27}{8}·\frac{5}{2}\right)=-\frac{135}{16}=-8\frac{7}{16}$

Ответ: $\left(-3\frac{3}{8}\right)·2\frac{1}{2}=-8\frac{7}{16}$

Умножение отрицательных рациональных чисел

Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.

Необходимо найти произведение отрицательных рациональных чисел $-3,146$ и $-56$.

Решение: модули заданных чисел соответственно равны $3,146$ и $56$.

Перемножим их столбиком:

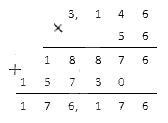
Полученный результат и будет являться искомым произведением.

Ответ: $(-3,146) · (-56) = 176,176$

Деление рациональных чисел

Деление – действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенства$b·c =a$ следует, что $a:b =c$ и $a:c=b$. И наоборот: из равенств $a:b=c$ и $a:c=b$ следует, что$b·c=a$.

На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.

Разделить число $а$ на число $b$, отличное от нуля – то же самое, что умножить число$a$ на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: $a:b=a·b^{-1}$.

Указанное равенство доказывается просто: на основе свойств действий с рациональными числами справедливой будет цепочка равенств $(a·b-1)· b=a·(b-1·b)=a·1=a$, которая и доказывает равенство $a : b = a · b^{-1}$.

Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.

Необходимо выполнить действие деления $3\frac{1}{3}:\left(-1\frac{1}{6}\right)$

Решение

Определим число, обратное заданному делителю. Запишем заданный делитель в виде неправильной дроби: $-1\frac{1}{6}= -\frac{7}{6}$.

Число, обратное этой дроби, будет:$-\frac{6}{7}$. Теперь, согласно вышеуказанному правилу, произведем действие умножения рациональных чисел: $3\frac{1}{3}-1\frac{1}{6}=3\frac{1}{3}·-\frac{6}{7}=\frac{10}{3}·(-\frac{6}{7}) =-(\frac{10}{3}·\frac{6}{7})=-\frac{20}{7}= -2\frac{6}{7}$

Ответ: $3\frac{1}{3}:\left(-1\frac{1}{6}\right)=-2\frac{6}{7}$