Деление натуральных чисел: правила, примеры, решения

В этой статье мы рассмотрим правила и алгоритмы деления натуральных чисел. Сразу отметим, что здесь мы смотрим только на деление нацело, то есть без остатка. О делении натуральных чисел с остатком читайте в нашем отдельном материале.

Перед тем, как формулировать правило деления натуральных чисел, нужно понять связь деления с умножением. После того, как мы установим эту связь, последовательно рассмотрим самые простые случаи: деление натурального числа на себя и на единицу. Далее разберем деление с помощью таблицы умножения, деление методом последовательного вычитания, деление на числа, кратные числу $10$, различные степени числа $10$.

Для каждого случая приведем и подробно рассмотрим примеры. В конце статьи покажем, как проводить проверку результата деления.

Связь деления с умножением

Чтобы проследить связь между делением и умножением, вспомним, что деление представляется, как разбиение исходного делимого множества на несколько одинаковых множеств. Умножение связано с объединением нескольких одинаковых множеств в одно. 

Деление - действие, обратное умножению. Что это значит? Приведем аналогию. Представим, что у нас есть $b$ множеств, в каждом из которых - по $с$ предметов. Общее количество предметов во всех множествах равно $a$. Умножение - это объединение всех множеств в одно. Математически оно запишется так:

$b·c=a$.

Обратный процесс разбиения полученного общего множества на $b$ множеств по $с$ предметов в каждом соответствует делению:

$a÷b=c$.

На основе сказанного можно перейти к следующему утверждению:

Если произведение натуральных чисел $c$ и $b$ равно $a$, то частное чисел $a$ и $b$ равно $c$. Перепишем в буквенном виде. 

Если $b·c=a$, то $a÷b=c$

Пользуясь переместительным свойством умножения, можно записать:

$c·b=a$

Отсюда также следует, что $a÷с=b$. 

На основании сказанного можно сформулировать общий вывод. Если произведение чисел $c$ и $b$ равно $a$, то соответственно частные $a÷b$ и $a÷c$ равны $c$ и $b$.

Подытожим все изложенное выше и дадим определение деления натуральных чисел.

Это определение станет базой, на основе которой мы будем строить правила и методы деления натуральных чисел.

Деление методом последовательного вычитания

Только что мы говорили о делении в контексте умножения. На основе этого знания можно проводить операцию деления. Однако, существует еще один, достаточно простой и достойный внимания подход - деление методом последовательного вычитания. Этот способ понятен интуитивно, поэтому рассмотрим его на примере, не приводя теоретических выкладок.

Работая с числами, не нужно каждый раз проводить аналогию с предметами. Что мы делали с делимым и делителем? Последовательно вычитали делитель из делимого, пока не получили нуль в остатке.

Для закрепления рассмотрим еще один, более сложный пример.

Отметим, что данный метод удобен только в случаях, когда необходимое количество последовательных вычитаний невелико. В остальных случаях целесообразно применять правила деления, которые мы рассмотрим ниже.

Деление равных натуральных чисел

Согласно свойствам натуральных чисел, сформулируем правило, как делить равные натуральные числа.

Например:

$1÷1=1$; $141÷141=1$; $2589÷2589=1$; $100000000÷100000000=1$.

Деление на единицу

Основываясь на свойствах натуральных чисел, можно также сформулировать правило деление натурального числа на единицу.

Например: 

$1÷1=1$; $141÷1=141$; $2589÷1=2589$; $100000000÷1=100000000$.

Деление с помощью таблицы умножения

Таблица умножения - удобный инструмент, который позволяет найти произведения однозначных натуральных чисел. Однако, ее можно использовать и для деления.

Таблица умножения позволяет находить не только результат произведения множителей, но и множитель по известному произведению и другому множителю. Как мы выяснили ранее, деление - это как раз и есть нахождение неизвестного множителя по известному произведению и еще одному множителю. 

С помощью таблицы умножения можно проводить деление любого числа на желтом фоне на любое однозначное натуральное число. Покажем, как это делать. Есть два способа, применение которых мы будем рассматривать на примерах.

Разделим $48$ на $6$.

Способ первый.

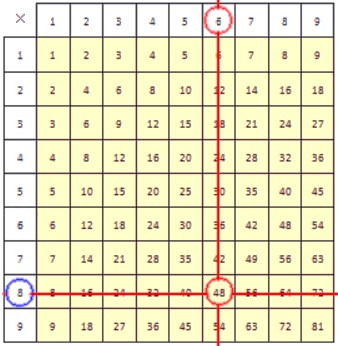
В столбце, верхняя ячейка которого содержит делитель $6$, находим делимое $48$. Результат деления при этом находится в крайней левой ячейке строки, содержащей делимое. Он обведен синей окружностью.

Способ второй. 

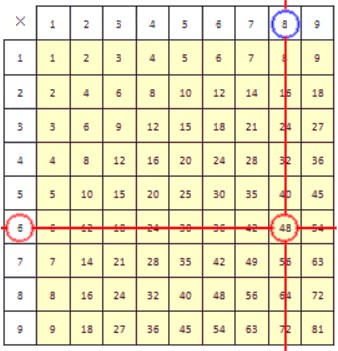
Сначала в строке с делителем $6$ находим делимое $48$. Результат деления при этом находится в крайней верхней ячейке столбца, содержащем делимое. Он обведен синей окружностью.

Итак, мы разделили $48$ на $6$ и получили $8$. Результат был найден по таблице умножения двумя способами. Оба способа абсолютно идентичны.

Для закрепления рассмотрим еще один пример. Разделим $7$ на $1$. Приведем рисунки, иллюстрирующие процесс деления.

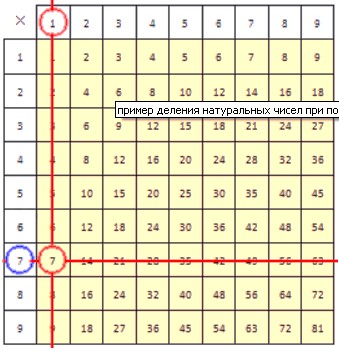
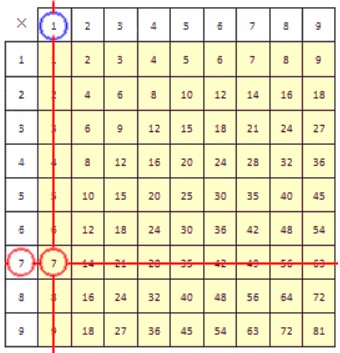
В результате деления числа 7  на  1, как вы уже догадались, получается число $7$. В делении с помощью таблицы умножения очень важно знать эту таблицу наизусть, так как не всегда можно иметь ее под рукой.

Настоятельно рекомендуем выучить таблицу умножения!

Деление на 10, 100, 1000 и т.д.

Сразу сформулируем правило деления на натуральных чисел на $10, 100, 1000$ и т.д. Сразу будем считать, что деление без остатка возможно.

Например, $30÷10=3$. От числа $30$ мы отбросили один нуль.

Частное $120000÷1000$ равно $120$ - от числа $120000$ отбрасываем справа три нуля, именно столько их содержится в делителе.

Обоснование правила строится на правиле умножения натурального числа на $10, 100, 1000$ и т.д. Приведем пример. Пусть нужно разделить $10200$ на $100$.

$10200=102·100$

$10200÷100=\frac{102·100}{100}=102$.

Представление делимого в виде произведения

При делении натуральных чисел не стоит забывать о свойстве деления произведения двух чисел на натуральное число. Иногда делимое можно представить в виде произведения, один из множителей в котором делится на делитель. 

Рассмотрим типичные случаи.

Приведем еще несколько аналогичных примеров.

В более сложных примерах удобно пользоваться таблицей умножения. Проиллюстрируем это.

Для закрепления данного материала рассмотрим еще один пример, уже без подробных словесных пояснений.

Деление натуральных чисел, оканчивающихся на нуль

При делении чисел, записи которых оканчиваются цифрой $0$, полезно помнить свойство деления натурального числа на произведение двух чисел. При этом, делитель представляется в виде произведения двух множителей, после чего указанное свойство находит применение в совокупности с таблицей умножения.

Как всегда, поясним это на примерах.

Для закрепления разберем еще один, более сложный пример.

Подведем итог по изложенному в данном пункте.

Метод подбора частного

Прежде чем рассматривать этот способ деления, введем некоторые условия.

Пусть числа $a$ и $b$ делятся друг на друга, причем произведение $b·10$ дает число, большее, чем $a$. В таком случае частное $a÷b$ является однозначным натуральным числом. Иными словами, это число от $1$ до $9$. Это типичная ситуация, когда метод подбора частного удобен и применим. Последовательно умножая делитель на $1, 2, 3, .. , 9$ и сравнивая результат с делимым, можно найти частное.

Рассмотрим пример.

Отметим, что в случаях, когда $b·10>a$ частное также удобно находить методом последовательного вычитания.

Представление делимого в виде суммы

Еще один способ, который может помочь найти частное - это представить делимое в виде суммы нескольких натуральных чисел, каждое из которых легко делится на делитель. После этого нам пригодится свойство деления суммы натуральных чисел на число. Вместе с примером рассмотрим алгоритм и ответим на вопрос: в виде каких слагаемых представлять делимое?

Пусть делимое равно $8551$, а делитель равен $17$.

1. Вычислим, на сколько в записи делимого больше знаков, чем в записи делителя. В нашем случае делитель содержит два знака, а делимое - четыре. Значит в записи делимого на два знака больше. Запоминаем число $2$.
2. Справа в делителе дописываем два нуля. Почему два? В предыдущем пункте мы как раз и определили это число. Однако, если записанное в результате число окажется больше делителя, из числа, полученного в предыдущем пункте, нужно вычесть $1$. В нашем примере, дописав нули к делителю, мы получили число $1700<8551$. Таким образом, отнимать единицу из двойки, полученной в первом пункте, не нужно. В памяти так же оставляем число $2$.
3. К числу $1$ справа приписываем нули в количестве, определенном числом из предыдущего пункта. Тем самым мы получаем рабочую единицу разряда, с которым будем оперировать далее. В нашем случае, к единице приписываются два нуля. Рабочий разряд - сотни. 
4. Проводим последовательное умножения делителя на $1, 2, 3$ и т.д. единицы рабочего разряда до того момента, пока не получим число, большее, чем делимое. $17·100=1700; 17·200=3400; 17·300=5100; 17·400=6400; 17·500=8500; 17·600=10200$Нас интересует предпоследний результат, так как следующий после него результат произведения больше делимого. Число $8500$, которое получено на предпоследнем шаге при умножении, и является первым слагаемым. Запоминаем равенство, которое мы будем использовать далее: $8500=17·500$.
5. Вычисляем разность между делимым и найденным слагаемым. Если она не равна нулю, возвращаемся к первому пункту и начинаем поиск второго слагаемого, используя вместо делимого уже полученную разность. Повторяем пункты до тех пор, пока в результате не получим нуль. В нашем примере разность равна $8551-8500=51$. $51\ne 0$, поэтому, переходим к пункту $1$.

Повторяем алгоритм:

1. Сравниваем количество знаков в новом делимом $51$ и делителе $17$. В обоих записях по две цифры, разность количества знаков равно нулю. Запоминаем число $0$.
2. Так как мы запомнили число $0$, в записи делителя не нужно дописывать дополнительных нулей.
3. К единице также не будем добавлять нулей. Опять же, потому что в первом пункте мы запоминали число $0$. Таким образом, нашим рабочим разрядом являются единицы
4. Последовательно умножаем $17$ на $1, 2, 3,..$ и т.д. Получаем: $17·1=17; 17·2=34; 17·3=51$.
5. Очевидно, на третьем шаге мы получили число, равное делителю. Это и есть второе слагаемое. Так как $51-51=0$, на этом этапе останавливаем поиск слагаемых - он завершен.

Теперь осталось найти частное. Делимое $8551$ мы представили в виде суммы $8500+51$. Запишем:

$\left(8500+51\right)÷17=\left(8500÷17\right)+\left(51÷17\right)$.

Результаты делений в скобках известны нам из проведенных ранее действий.

$\left(8500+51\right)÷17=\left(8500÷17\right)+\left(51÷17\right)=500+3=503$.

Результат деления: $8551÷17=503$.

Рассмотрим еще несколько примеров, уже не комментируя каждое действие столь детально.

Постепенно увеличиваем сложность примеров.

Казалось бы, мы рассмотрели практически все возможные способы деления натуральных чисел. На этом, тему можно считать закрытой. Однако, есть способ, который в ряде случаев позволяет провести деление быстрее и рациональнее.

Рассмотрим его напоследок.

Представление делимого в виде разности натуральных чисел

Иногда делимое проще и удобнее представлять в виде разности, а не суммы. Это может значительно ускорить и облегчить процесс деления. Как именно? Покажем на примере.

Решим еще один пример тем же методом. Отметим, что важно уметь правильно заметить, какую манипуляцию сделать с числами, чтобы провести деление легко. Скажем даже, что в этом присутствует некоторый элемент искусства.

Проверка результата деления

Проверка никогда не бывает лишней, особенно, если мы делили большие числа. Как проверять, правильно ли выполнено деление натуральных чисел? При помощи умножения!

Смысл этого действия очень прост. Например, у нас было $a$ предметов, и эти $a$ предметов мы разложили на $b$ кучек. В каждой кучке оказалось по $с$ предметов. Математически это выглядит так:

$a÷b=c$.

Теперь объединим обратно все $b$ кучек по $с$ предметов. В результате должно получится та же совокупность предметов $a$.

$b·c=a$.

Рассмотрим проведение проверки на двух примерах.

Проверка результата деления чисел делением

Рассмотренный выше способ проверки основан на умножении. Существует также проверка делением. Как ее проводить?

Правило основано на той же связи между делимым, делителем и частным, что и правило из предыдущего пункта.

Рассмотрим примеры.