- 16 июля 2025
- 5 минут
- 2 623
Сложение отрицательных чисел: правило, примеры
Статью подготовили специалисты образовательного сервиса Zaochnik.
В рамках этого материала мы затронем такую важную тему, как сложение отрицательных чисел. В первом параграфе мы расскажем основное правило для этого действия, а во втором – разберем конкретные примеры решения подобных задач.
Основное правило сложения натуральных чисел
Перед тем, как вывести правило, вспомним, что мы вообще знаем о положительных и отрицательных числах. Ранее мы условились, что отрицательные числа нужно воспринимать как долг, убыток. Модуль отрицательного числа выражает точные размеры этого убытка. Тогда сложение отрицательных чисел можно представить как сложение двух убытков.
Воспользовавшись этим рассуждением, сформулируем основное правило сложения отрицательных чисел.
Для того чтобы выполнить сложение отрицательных чисел, нужно сложить значения их модулей и поставить минус перед полученным результатом. В буквенном виде формула выглядит как .
Исходя из этого правила, можно сделать вывод, что сложение отрицательных чисел аналогично сложению положительных, только в итоге у нас обязательно должно получиться отрицательное число, ведь перед суммой модулей надо ставить знак минус.
Какие можно привести доказательства этого правила? Для этого нам потребуется вспомнить основные свойства действий с действительными числами (или с целыми, или с рациональными –они одинаковы для всех этих типов чисел). Для доказательства нам нужно всего лишь продемонстрировать, что разность левой и правой части равенства будет равна .
Вычесть одно число из другого – это то же самое, что и прибавить к нему такое же противоположное число. Следовательно, . Вспомним, что числовые выражения со сложением обладают двумя основными свойствами – сочетательным и переместительным. Тогда мы можем сделать вывод, что . Поскольку, сложив противоположные числа, мы всегда получаем , то .Наше равенство можно считать доказанным, значит, и правило сложения отрицательных чисел мы тоже доказали.
Задачи на сложение отрицательных чисел
Во втором параграфе мы возьмем конкретные задачи, где нужно складывать отрицательные числа, и попробуем применить в них изученное правило.
Найдите сумму двух отрицательных чисел и .
Решение
Выполним действия пошагово. Сначала нам надо найти модули складываемых чисел: . Далее нам нужно выполнить действие сложения, для чего мы используем метод подсчета столбиком:
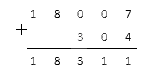
Все, что нам осталось, – это поставить минус перед результатом и получить .
Ответ: - .
От того, какие у нас числа, зависит, к чему мы можем свести действие сложения: к нахождению суммы натуральных чисел, к сложению обыкновенных или десятичных дробей. Разберем задачу с такими числами.
Найдите сумму двух отрицательных чисел и .
Решение
Находим модули искомых чисел и получаем и . У нас получились две разные дроби. Сведем задачу к сложению двух обыкновенных дробей, для чего представим периодическую дробь в виде обыкновенной:
В итоге мы получили дробь, которую будет легко сложить с первым исходным слагаемым (если вы забыли, как правильно складывать дроби с разными знаменателями, повторите соответствующий материал).
В итоге мы получили смешанное число, перед которым нам осталось только поставить минус. На этом расчеты завершены.
Ответ: .
Действительные отрицательные числа складываются аналогичным образом. Результат такого действия принято записывать числовым выражением. Его значение можно и не вычислять или ограничиться примерными расчетами. Так, к примеру, если нам надо найти сумму , то ответ мы записываем как . Сложению действительных чисел мы посвятили отдельный материал, в котором можно найти и другие примеры.
Математические онлайн-калькуляторы




