Параметрические уравнения прямой на плоскости: описание, примеры, решение задач

Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.

Вывод параметрических уравнений прямой на плоскости

Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.

Допустим, нам задана прямоугольная система координат $Oxy$. А также заданы прямая а с указанием лежащей на ней точки ${М}_1(x_1, y_1)$ и направляющий вектор заданной прямой $\overrightarrow{a}= (a_x, a_y)$. Дадим описание заданной прямой $a$, используя уравнения.

Используем произвольную точку $М (x, y)$ и получим вектор $\overrightarrow{{М}_1М}$; вычислим его координаты по координатам точек начала и конца: $\overrightarrow{M_{1}M}=(x-x_1, y-y_1)$. Опишем полученное: прямая задана множеством точек $М (x, y)$, проходит через точку ${М}_1(x_1, y_1)$ и имеет направляющий вектор $\overrightarrow{a}= (a_x, a_y)$. Указанное множество задает прямую только тогда, когда векторы $\overrightarrow{M_{1}M}=(x-x_1, y-y_1)$ и $\overrightarrow{a}= (a_x, a_y)$ являются коллинеарными.

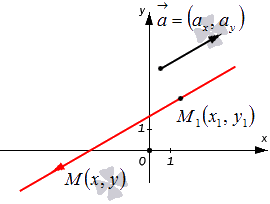
Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов $\overrightarrow{M_{1}M}=(x-x_1, y-y_1)$ и $\overrightarrow{a}= (a_x, a_y)$ возможно записать в виде уравнения:

$\overrightarrow{M_{1}M}=\lambda ·\overrightarrow{a}$, где $\lambda$ – некоторое действительное число.

Уравнение $\overrightarrow{M_{1}M}=\lambda ·\overrightarrow{a}$ называют векторно-параметрическим уравнением прямой.

В координатной форме оно имеет вид:

$\overrightarrow{M_{1}M}=\lambda ·\overrightarrow{a}\iff open\begin{array}{l}x-x_1=\lambda ·a_x\\ y-y_1=\lambda ·a_y\end{array}\iff open\begin{array}{l}x=x_1+a_x·\lambda \\ y=y_1+a_y·\lambda \end{array}$

Уравнения полученной системы $open\begin{array}{l}x=x_1+a_x·\lambda \\ y=y_1+a_y·\lambda \end{array}$ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида $open\begin{array}{l}x=x_1+a_x·\lambda \\ y=y_1+a_y·\lambda \end{array}$ при переборе всех действительных значений параметра $\lambda$

Составление параметрических уравнений прямой на плоскости

Согласно вышесказанному, параметрические уравнения прямой на плоскости $open\begin{array}{l}x=x_1+a_x·\lambda \\ y=y_1+a_y·\lambda \end{array}$ определяют прямую линию, которая задана в прямоугольной системе координат, проходит через точку ${М}_1(x_1, y_1)$ и имеет направляющий вектор $\overrightarrow{a}= (a_x, a_y)$. Следовательно, если заданы координаты некоторой точки прямой и координаты ее направляющего вектора, то возможно сразу записать параметрические уравнения заданной прямой.

Необходимо составить параметрические уравнения прямой на плоскости в прямоугольной системе координат, если заданы принадлежащая ей точка ${М}_1(2, 3)$ и ее направляющий вектор $\overrightarrow{a}= (\sqrt{3}, 1)$.

Решение

На основе исходных данных получим: $x_1 = 2, y_1 = 3, a_x = \sqrt{3}, a_y = 1$. Параметрические уравнения будут иметь вид:

$open\begin{array}{l}x=x_1+a_x·\lambda \\ y=y_1+a_{y·}\lambda \end{array}\iff open\begin{array}{l}x=2+\sqrt{3}·\lambda \\ y=3+1·\lambda \end{array}\iff open\begin{array}{l}x=2+\sqrt{3}·\lambda \\ y=3+\lambda \end{array}$

Наглядно проиллюстрируем:

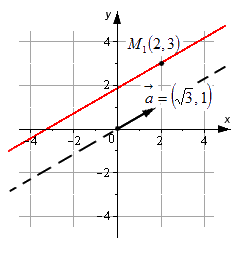
Ответ:$open\begin{array}{l}x=2+\sqrt{3}·\lambda \\ y=3+\lambda \end{array}$

Необходимо отметить: если вектор $\overrightarrow{a}=(a_x, a_y)$служит направляющим вектором прямой а, а точки ${М}_1(x_1, y_1)$ и ${М}_2(x_2, y_2)$ принадлежат этой прямой, то ее возможно определить, задав параметрическими уравнениями вида: $open\begin{array}{l}x=x_1+a_x·\lambda \\ y=y_1+a_y·\lambda \end{array}$, а также и таким вариантом: $open\begin{array}{l}x=x_2+a_x·\lambda \\ y=y_2+a_y·\lambda \end{array}$.

К примеру, нам заданы направляющий вектор прямой $\overrightarrow{a}= (2, -1)$, а также точки ${М}_1(1, -2)$ и ${М}_2 (3, -3)$, принадлежащие этой прямой. Тогда прямую определяют параметрические уравнения: $open\begin{array}{l}x=1+2·\lambda \\ y=-2-\lambda \end{array}$ или $open\begin{array}{l}x=3+2·\lambda \\ y=-3-\lambda \end{array}$ .

Следует обратить внимание и на такой факт: если $\overrightarrow{a}= (a_x, a_y)$- направляющий вектор прямой$a$, то ее направляющим векторомбудет и любой из векторов $\overrightarrow{\mu ·a}=(\mu ·a_x, \mu ·a_y)$, где $\mu ϵ R, \mu \ne 0$ .

Таким образом, прямая а на плоскости в прямоугольной системе координат может быть определена параметрическими уравнениями: $open\begin{array}{l}x=x_1+\mu ·a_x·\lambda \\ y=y_1+\mu ·a_y·\lambda \end{array}$ при любом значении $\mu$, отличном от нуля.

Допустим, прямая а задана параметрическими уравнениями $open\begin{array}{l}x=3+2·\lambda \\ y=-2-5·\lambda \end{array}$. Тогда $\overrightarrow{a}= (2, -5)$ - направляющий векторэтой прямой. А также любой из векторов $\mu ·\overrightarrow{a}=(\mu ·2, \mu ·\left(-5\right))=\left(2\mu , -5\mu \right), \mu \in R, \mu \ne 0$ станет направляющим вектором для заданной прямой. Для наглядности рассмотрим конкретный вектор$-2 · \overrightarrow{a}= (-4, 10)$, ему соответствует значение $\mu = -2$. В таком случае заданную прямую можно также определить параметрическими уравнениями $open\begin{array}{l}x=3-4·\lambda \\ y=-2+10·\lambda \end{array}$.

Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно

В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.

Параметрическим уравнениям прямой вида $open\begin{array}{l}x=x_1+a_x·\lambda \\ y=y_1+a_y·\lambda \end{array}$ будет соответствовать каноническое уравнение прямой на плоскости $\frac{x-x_1}{a_x}=\frac{y-y_1}{a_y}$.

Разрешим каждое из параметрических уравнений относительно параметра $\lambda$, приравняем правые части полученных равенств и получим каноническое уравнение заданной прямой:

$open\begin{array}{l}x=x_1+a_x·\lambda \\ y=y_1+a_y·\lambda \end{array}\iff open\begin{array}{l}\lambda =\frac{x-x_1}{a_x}\\ \lambda =\frac{y-y_1}{a_y}\end{array}\iff \frac{x-x_1}{a_x}=\frac{y-y_1}{a_y}$

При этом не должно смущать, если $a_x$ или $a_y$ будут равны нулю.

Необходимо осуществить переход от параметрических уравнений прямой $open\begin{array}{l}x=3\\ y=-2-4·\lambda \end{array}$ к каноническому уравнению.

Решение

Запишем заданные параметрические уравнения в следующем виде: $open\begin{array}{l}x=3+0·\lambda \\ y=-2-4·\lambda \end{array}$

Выразим параметр $\lambda$ в каждом из уравнений: $open\begin{array}{l}x=3+0·\lambda \\ y=-2-4·\lambda \end{array}\iff open\begin{array}{l}\lambda =\frac{x-3}{0}\\ \lambda =\frac{y+2}{-4}\end{array}$

Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:

$\frac{x-3}{0}=\frac{y+2}{-4}$

Ответ: $\frac{x-3}{0}=\frac{y+2}{-4}$

В случае, когда необходимо записать уравнение прямой вида $Ax+By+C=0$, при этом заданы параметрические уравнения прямой на плоскости, необходимо сначала осуществить переход к каноническому уравнению, а затем к общему уравнению прямой. Запишем всю последовательность действий:

$$\begin{gathered} open\begin{array}{l}x=x_1+a_x·\lambda \\ y=y_1+a_y·\lambda \end{array}\iff open\begin{array}{l}\lambda =\frac{x-x_1}{a_x}\\ \lambda =\frac{y-y_1}{a_y}\end{array}\iff \frac{x-x_1}{a_x}=\frac{y-y_1}{a_y}\iff \\ \iff a_y·(x-x_1)=a_x·(y-y_1)\iff Ax+By+C=0 \end{gathered}$$

Необходимо записать общее уравнение прямой, если заданы определяющие ее параметрические уравнения: $open\begin{array}{l}x=-1+2·\lambda \\ y=-3·\lambda \end{array}$

Решение

Для начала осуществим переход к каноническому уравнению:

$open\begin{array}{l}x=-1+2·\lambda \\ y=-3·\lambda \end{array}\iff open\begin{array}{l}\lambda =\frac{x+1}{2}\\ \lambda =\frac{y}{-3}\end{array}\iff \frac{x+1}{2}=\frac{y}{-3}$

Полученная пропорция идентична равенству $-3 · (x + 1) = 2 · y$. Раскроем скобки и получим общее уравнение прямой: $-3·\left(x+1\right)=2·y\iff 3x+2y+3=0$.

Ответ: $3x+2y+3=0$

Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.

Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.

Самый простой переход: от канонического уравнения к параметрическим. Пусть задано каноническое уравнение вида: $\frac{x-x_1}{a_x}=\frac{y-y_1}{a_y}$ . Каждое из отношений этого равенства примем равным параметру $\lambda$:

$\frac{x-x_1}{a_x}=\frac{y-y_1}{a_y}=\lambda \iff open\begin{array}{l}\lambda =\frac{x-x_1}{a_x}\\ \lambda =\frac{y-y_1}{a_y}\end{array}$

Разрешим полученные уравнения относительно переменных $x$ и $y$:

$open\begin{array}{l}x=x_1+a_x·\lambda \\ y=y_1+a_y·\lambda \end{array}$

Необходимо записать параметрические уравнения прямой, если известно каноническое уравнение прямой на плоскости: $\frac{x-2}{5}=\frac{y-2}{2}$

Решение

Приравняем части известного уравнения к параметру $\lambda$: $\frac{x-2}{5}=\frac{y-2}{2}=\lambda$ . Из полученного равенства получим параметрические уравнения прямой: $\frac{x-2}{5}=\frac{y-2}{2}=\lambda \iff open\begin{array}{l}\lambda =\frac{x-2}{5}\\ \lambda =\frac{y-2}{5}\end{array}\iff open\begin{array}{l}x=2+5·\lambda \\ y=2+2·\lambda \end{array}$

Ответ: $open\begin{array}{l}x=2+5·\lambda \\ y=2+2·\lambda \end{array}$

Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.

Необходимо записать параметрические уравнения прямой при известном общем уравнении этой прямой: $4x-3y-\sqrt{3}=0$ .

Решение 

Заданное общее уравнение преобразуем в уравнение канонического вида:

$$\begin{gathered} 4x-3y-\sqrt{3}=0\iff 4x=3y+\sqrt{3}\iff \\ \iff 4x=3\left(y+\frac{1}{\sqrt{3}}\right)\iff \frac{x}{3}=\frac{y+{\displaystyle \frac{1}{\sqrt{3}}}}{4} \end{gathered}$$

Приравняем обе части равенства к параметру $\lambda$ и получим требуемые параметрические уравнения прямой:

$\frac{x}{3}=\frac{y+{\displaystyle \frac{1}{\sqrt{3}}}}{4}=\lambda \iff open\begin{array}{l}\frac{x}{3}=\lambda \\ \frac{y+{\displaystyle \frac{1}{\sqrt{3}}}}{4}=\lambda \end{array}\iff open\begin{array}{l}x=3·\lambda \\ y=-\frac{1}{\sqrt{3}}+4·\lambda \end{array}$

Ответ: $open\begin{array}{l}x=3·\lambda \\ y=-\frac{1}{\sqrt{3}}+4·\lambda \end{array}$

Примеры и задачи с параметрическими уравнениями прямой на плоскости

Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.

1. В задачах первого типа заданы координаты точек, принадлежащих или нет прямой, описанной параметрическими уравнениями.

Решение таких задач опирается на следующий факт: числа $(x, y)$, определяемые из параметрических уравнений $open\begin{array}{l}x=x_1+a_x·\lambda \\ y=y_1+a_y·\lambda \end{array}$ при некотором действительном значении $\lambda$, являются координатами точки, принадлежащей прямой, которая описывается этими параметрическими уравнениями.

Необходимо определить координаты точки, которая лежит на прямой, заданной параметрическими уравнениями$open\begin{array}{l}x=2-\frac{1}{6}·\lambda \\ y=-1+2·\lambda \end{array}$ при $\lambda = 3$.

Решение 

Подставим в заданные параметрические уравнения известное значение $\lambda = 3$ и осуществим вычисление искомых координат: $open\begin{array}{l}x=2-\frac{1}{6}·3\\ y=-1+2·3\end{array}\iff open\begin{array}{l}x=1\frac{1}{2}\\ y=5\end{array}$

Ответ: $\left(1\frac{1}{2}, 5\right)$

Также возможна следующая задача: пусть задана некоторая точка $M_0 (x_0, y_0)$ на плоскости в прямоугольной системе координат и нужно определить, принадлежит ли эта точка прямой, описываемой параметрическими уравнениями $open\begin{array}{l}x=x_1+a_x·\lambda \\ y=y_1+a_y·\lambda \end{array}$.

Чтобы решить подобную задачу, необходимо подставить координаты заданной точки в известные параметрические уравнения прямой. Если будет определено, что возможно такое значение параметра $\lambda = {\lambda }_0$, при котором будут верными оба параметрических уравнения, тогда заданная точка является принадлежащей заданной прямой.

Заданы точки ${М}_0(4, -2)$ и $N_0(-2, 1)$. Необходимо определить, являются ли они принадлежащими прямой, определенной параметрическими уравнениями $open\begin{array}{l}x=2·\lambda \\ y=-1-\frac{1}{2}·\lambda \end{array}$.

Решение

Подставим координаты точки ${М}_0(4, -2)$ в заданные параметрические уравнения:

$open\begin{array}{l}4=2·\lambda \\ -2=-1-\frac{1}{2}·\lambda \end{array}\iff open\begin{array}{l}\lambda =2\\ \lambda =2\end{array}\iff \lambda =2$

Делаем вывод, что точка ${М}_0$ принадлежит заданной прямой, т.к. соответствует значению $\lambda = 2$.

Далее по аналогии проверим заданную точку $N_0(-2, 1)$, подставив ее координаты в заданные параметрические уравнения:

$open\begin{array}{l}-2=2·\lambda \\ 1=-1-\frac{1}{2}·\lambda \end{array}\iff open\begin{array}{l}\lambda =-1\\ \lambda =-4\end{array}$

Очевидно, что не существует такого параметра $\lambda$, которому будет соответствовать точка $N_0$. Другими словами, заданная прямая не проходит через точку $N_0(-2, 1)$.

Ответ: точка ${М}_0$ принадлежит заданной прямой; точка $N_0$ не принадлежит заданной прямой.

2. В задачах второго типа требуется составить параметрические уравнения прямой на плоскости в прямоугольной системе координат. Самый простой пример такой задачи (при известных координатах точки прямой и направляющего вектора) был рассмотрен выше. Теперь разберем примеры, в которых сначала нужно найти координаты направляющего вектора, а потом записать параметрические уравнения.

Задана точка $M_1\left(\frac{1}{2}, \frac{2}{3}\right)$. Необходимо составить параметрические уравнения прямой, проходящей через эту точку и параллельной прямой $\frac{x}{2}=\frac{y-3}{-1}$.

Решение

По условию задачи прямая, уравнение которой нам предстоит опередить, параллельна прямой $\frac{x}{2}=\frac{y-3}{-1}$. Тогда в качестве направляющего вектора прямой, проходящей через заданную точку, возможно использовать направляющий вектор прямой $\frac{x}{2}=\frac{y-3}{-1}$, который запишем в виде: $\overrightarrow{a}=(2, -1)$. Теперь известны все необходимые данные для того, чтобы составить искомые параметрические уравнения:

$open\begin{array}{l}x=x_1+a_x·\lambda \\ y=y_1+a_y·\lambda \end{array}\iff open\begin{array}{l}x=\frac{1}{2}+2·\lambda \\ y=\frac{2}{3}+(-1)·\lambda \end{array}\iff open\begin{array}{l}x=\frac{1}{2}+x·\lambda \\ y=\frac{2}{3}-\lambda \end{array}$

Ответ: $open\begin{array}{l}x=\frac{1}{2}+x·\lambda \\ y=\frac{2}{3}-\lambda \end{array}$.

Задана точка ${М}_1(0, -7)$. Необходимо записать параметрические уравнения прямой, проходящей через эту точку перпендикулярно прямой $3x – 2y – 5 = 0$.

Решение

В качестве направляющего вектора прямой, уравнение которой надо составить, возможно взять нормальный вектор прямой $3x – 2y – 5 = 0$. Его координаты $(3, -2)$. Запишем требуемые параметрические уравнения прямой:

$open\begin{array}{l}x=x_1+a_x·\lambda \\ y=y_1+a_y·\lambda \end{array}\iff open\begin{array}{l}x=0+3·\lambda \\ y=-7+(-2)·\lambda \end{array}\iff open\begin{array}{l}x=3·\lambda \\ y=-7-2·\lambda \end{array}$

Ответ: $open\begin{array}{l}x=3·\lambda \\ y=-7-2·\lambda \end{array}$

3. В задачах третьего типа требуется осуществить переход от параметрических уравнений заданной прямой к прочим видам уравнений, которые ее определяют. Решение подобных примеров мы рассматривали выше, приведем еще один.

Дана прямая на плоскости в прямоугольной системе координат, определяемая параметрическими уравнениями $open\begin{array}{l}x=1-\frac{3}{4}·\lambda \\ y=-1+\lambda \end{array}$. Необходимо найти координаты какого-либо нормального вектора этой прямой.

Решение

Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:

$$\begin{gathered} open\begin{array}{l}x=1-\frac{3}{4}·\lambda \\ y=-1+\lambda \end{array}\iff open\begin{array}{l}\lambda =\frac{x-1}{-{\displaystyle \frac{3}{4}}}\\ \lambda =\frac{y+1}{1}\end{array}\iff \frac{x-1}{-{\displaystyle \frac{3}{4}}}=\frac{y+1}{1}\iff \\ \iff 1·\left(x-1\right)=-\frac{3}{4}·\left(y+1\right)\iff x+\frac{3}{4}y-\frac{1}{4}=0 \end{gathered}$$

Коэффициенты переменных x и y дают нам требуемые координаты нормального вектора. Таким образом, нормальный вектор прямой $open\begin{array}{l}x=1-\frac{3}{4}·\lambda \\ y=-1+\lambda \end{array}$ имеет координаты $\left(1, \frac{3}{4}\right)$.

Ответ: $\left(1, \frac{3}{4}\right)$.