Перпендикулярные прямая и плоскость, признак и условия перпендикулярности прямой и плоскости

Содержание:

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Статья раскрывает понятие о перпендикулярности прямой и плоскости, дается определение прямой, плоскости, графически иллюстрировано и показано обозначение перпендикулярных прямой и плоскости. Сформулируем признак перпендикулярности прямой с плоскостью. Рассмотрим условия, при которых прямая и плоскость будут перпендикулярны с заданными уравнениями в плоскости и трехмерном пространстве. Все будет показано на примерах.

Перпендикулярные прямая и плоскость – основные сведения

Определение 1

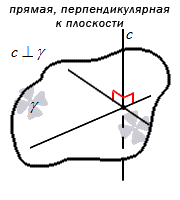
Прямая перпендикулярна к плоскости, когда она перпендикулярна к любой прямой, лежащей в этой плоскости.

Верно то, что и плоскость перпендикулярна к прямой, как и прямая к плоскости.

Перпендикулярность обозначается « $⊥$ ». Если в условии задано, что прямая $с$ перпендикулярна плоскости $γ$ , тогда запись имеет вид $с ⊥ γ$ .

Перпендикулярные прямая и плоскость – основные сведения

Например, если прямая перпендикулярна к плоскости, тогда возможно провести только одну прямую, благодаря которой две смежных стены комнаты пересекутся. Прямая считается перпендикулярной к плоскости потолка. Канат, расположенный в спортзале рассматривается в качестве отрезка прямой, который перпендикулярен плоскости, в данном случае полу.

При наличии перпендикулярной прямой к плоскости, угол между прямой и плоскостью считается прямым, то есть равен $90$ градусов.

Перпендикулярность прямой и плоскости – признак и условия перпендикулярности

Для нахождения выявления перпендикулярности необходимо использовать достаточное условие перпендикулярности прямой и плоскости. Оно гарантирует выполнение перпендикулярности прямой и плоскости. Данное условие считается достаточным и называют признаком перпендикулярности прямой и плоскости.

Теорема 1

Для перпендикулярности заданных прямой и плоскости достаточно, чтобы прямая была перпендикулярна двум пересекающимся прямым, которые лежат в этой плоскости.

Подробное доказательство приведено в учебнике геометрии $10 - 11$ класса. Теорема применяется для решения задач, где необходимо установить перпендикулярность прямой и плоскости.

Теорема 2

При условии параллельности хоть одной из прямых плоскости, считается, что вторая прямая также перпендикулярна к данной плоскости.

Признак перпендикулярности прямой и плоскости рассматривается еще со школы, когда необходимо решить задачи по геометрии. Рассмотрим подробнее еще одно необходимое и достаточное условие, при котором прямая и плоскость будут перпендикулярны.

Теорема 3

Для того, чтобы прямая а была перпендикулярна плоскости $γ$ , необходимым и достаточным условием является коллинеарность направляющего вектора прямой а и нормального вектора плоскости $γ$ .

Доказательство

При $\vec{a} = (a_{x}, a_{y}, a_{z})$ являющимся вектором прямой $a$ , при $\vec{n} = (n_{x}, n_{y}, n_{z})$ являющимся нормальным вектором плоскости $γ$ для выполнения перпендикулярности нужно, чтобы прямая $a$ и плоскость $γ$ принадлежали выполняемости условия коллинеарности векторов $\vec{a} = (a_{x}, a_{y}, a_{z})$ и $\vec{n} = (n_{x}, n_{y}, n_{z})$ . Отсюда получаем, что $\vec{a} = t \cdot \vec{n} \Leftrightarrow \{\begin{cases} \begin{array}{l} a_{x} = t \cdot n_{x} \\ a_{y} = t \cdot n_{y} \end{array} \\ a_{z} = t \cdot n_{z} \end{cases}$ , $t$ является действительным числом.

Данное доказательство основывается на необходимом и достаточном условии перпендикулярности прямой и плоскости, направляющего вектора прямой и нормального вектора плоскости.

Данное условие применимо для доказательства перпендикулярности прямой и плоскости, так как достаточно найти координаты направляющего вектора прямой и координаты нормального вектора в трехмерном пространстве, после чего производить вычисления. Используется для случаев, когда прямая определена уравнением прямой в пространстве, а плоскость уравнением плоскости некоторого вида.

Пример 1

Доказать перпендикулярность заданной прямой $\frac{x}{\sqrt{2} - 1} = \frac{y - 1}{2} = \frac{z + 2}{\sqrt{2} - 7}$ с плоскостью $x + 2 (\sqrt{2} + 1) y - (5 + 6 \sqrt{2}) z$ .

Решение

Знаменатели канонических уравнений являются координатами направляющего вектора данной прямой. Отсюда имеем, что $\vec{a} = (\sqrt{2} - 1, 2, \sqrt{2} - 7)$ является направляющим вектором прямой $\frac{x}{\sqrt{2} - 1} = \frac{y - 1}{2} = \frac{z + 2}{\sqrt{2} - 7}$ .

В общем уравнении плоскости коэффициенты перед переменными $x, y, z$ являются координатами нормального вектора данной плоскости. Отсюда следует, что $\vec{n} = (1, 2 (\sqrt{2} + 1), - (5 + 6 \sqrt{2}))$ - это нормальный вектор плоскости $x + 2 (\sqrt{2} + 1) y - (5 + 6 \sqrt{2}) z - 4 = 0$

Необходимо произвести проверку выполнимости условия. Получаем, что

$\{\begin{cases} \begin{array}{l} \sqrt{2} - 1 = t \cdot 1 \\ 2 = t \cdot 2 (\sqrt{2} + 1) \end{array} \\ \sqrt{2} = t \cdot (- (5 + 6 \sqrt{2})) \end{cases} \Leftrightarrow t = \sqrt{2} - 1$ , тогда векторы $\vec{a}$ и $\vec{n}$ связаны выражением $\vec{a} = (\sqrt{2} - 1) \cdot \vec{n}$ .

Это и есть коллинеарность векторов. отсюда следует, что прямая $\frac{x}{\sqrt{2} - 1} = \frac{y - 1}{2} = \frac{z + 2}{\sqrt{2} - 7}$ перпендикулярна плоскости $x + 2 (\sqrt{2} + 1) y - (5 + 6 \sqrt{2}) z - 4 = 0$ .

Ответ: прямая и плоскость перпендикулярны.

Пример 2

Определить, перпендикулярны ли прямая $\{\begin{cases} y - 1 = 0 \\ x + 4 z - 2 = 0 \end{cases}$ и плоскость $\frac{x}{\frac{1}{2}} + \frac{z}{- \frac{1}{2}} = 1$ .

Решение

Чтобы ответить на вопрос перпендикулярности, необходимо, чтобы было выполнено необходимое и достаточное условие, то есть для начала нужно найти вектор заданной прямой и нормальный вектор плоскости.

Из прямой $\{\begin{cases} y - 1 = 0 \\ x + 4 z - 2 = 0 \end{cases}$ видно, что направляющий вектор $\vec{a}$ - это произведение нормальных векторов плоскости $y - 1 = 0$ и $x + 4 z - 2 = 0$ .

Отсюда получаем, что $\vec{a} = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ 0 & 1 & 0 \\ 1 & 0 & 4 \end{matrix}| = 4 \cdot \vec{i} - \vec{k}$ .

Координаты вектора $\vec{a} = (4, 0, - 1)$ .

Уравнение плоскости в отрезках $\frac{x}{\frac{1}{2}} + \frac{z}{- \frac{1}{2}} = 1$ является эквивалентным уравнению плоскости $2 x - 2 z - 1 = 0$ , нормальный вектор которой равен $\vec{n} = (2, 0, - 2)$ .

Следует произвести проверку на коллинеарность векторов $\vec{a} = (4, 0, - 1)$ и $\vec{n} = (2, 0, - 2)$ .

Для этого запишем:

$\{\begin{cases} \begin{array}{l} 4 = t \cdot 2 \\ 0 = t \cdot 0 \end{array} \\ - 1 = t \cdot (- 2) \end{cases} \Leftrightarrow \{\begin{cases} \begin{array}{l} t = 2 \\ t \in R \Leftrightarrow t \in \emptyset \end{array} \\ t = \frac{1}{2} \end{cases}$

Отсюда делаем вывод о том, что направляющий вектор прямой не коллинеарен нормальному вектору плоскости. Значит, $\{\begin{cases} y - 1 = 0 \\ x + 4 z - 2 = 0 \end{cases}$ - это прямая, не перпендикулярная к плоскости $\frac{x}{\frac{1}{2}} + \frac{z}{- \frac{1}{2}}$ .

Ответ: прямая и плоскость не перпендикулярны.

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.