Перпендикулярные прямые, условие перпендикулярности прямых

Содержание:

18 марта 2023
10 минут
2598

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

В статье рассматривается вопрос о перпендикулярных прямых на плоскости и трехмерном пространстве. Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.

Перпендикулярные прямые – основные сведения

Угол между пересекающимися прямыми в пространстве может быть прямым. Тогда говорят, что данные прямые перпендикулярные. Когда угол между скрещивающимися прямыми прямой, тогда прямые также являются перпендикулярными. Отсюда следует, что перпендикулярные прямые на плоскости пересекающиеся, а перпендикулярные прямые пространства могут быть пересекающимися и скрещивающимися.

То есть понятия «прямые $a$ и $b$ перпендикулярны» и «прямые $b$ и $a$ перпендикулярны» считаются равноправными. Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.

Определение 1

Две прямые называют перпендикулярными, если угол при их пересечении дает $90$ градусов.

Перпендикулярность обозначается « $⊥$ », а запись принимает вид $a ⊥ b$ , что значит, прямая $a$ перпендикулярна прямой $b$ .

Перпендикулярные прямые – основные сведения

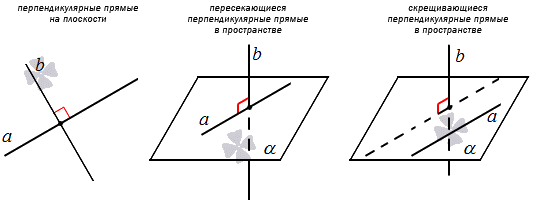
Например, перпендикулярными прямыми на плоскости могут быть стороны квадрата с общей вершиной. В трехмерном пространстве прямые $O_{x}, O_{z}, O_{y}$ перпендикулярны попарно: $O_{x}$ и $O_{z}$ , $O_{x}$ и $O_{y}$ , $O_{y}$ и $O_{z}$ .

Перпендикулярность прямых – условия перпендикулярности

Свойства перпендикулярности необходимо знать, так как большинство задач сводится к его проверке для последующего решения. Бывают случаи, когда о перпендикулярности идет речь еще в условии задания или когда необходимо пользоваться доказательством. Для того, чтобы доказать перпендикулярность достаточно, чтобы угол между прямыми был прямым.

Для того, чтобы определить их перпендикулярность при известных уравнениях прямоугольной системы координат, необходимо применить необходимое и достаточное условие перпендикулярности прямых. Рассмотрим формулировку.

Теорема 1

Для того, чтобы прямые $a$ и $b$ были перпендикулярными, необходимо и достаточно, чтобы направляющий вектор прямой обладал перпендикулярностью относительно направляющего вектора заданной прямой $b$ .

Само доказательство основывается на определении направляющего вектора прямой и на определении перпендикулярности прямых.

Доказательство 1

Пусть введена прямоугольная декартова система координат $О х у$ с заданными уравнениями прямой на плоскости, которые определяют прямые $a$ и $b$ . Направляющие векторы прямых $a$ и $b$ обозначим $\vec{a}$ и $\vec{b}$ . Из уравнения прямых $a$ и $b$ необходимым и достаточным условием является перпендикулярность векторов $\vec{a}$ и $\vec{b}$ . Это возможно только при скалярном произведении векторов $\vec{a} = (a_{x}, a_{y})$ и $\vec{b} = (b_{x}, b_{y})$ равном нулю, а запись имеет вид $(\vec{a}, \vec{b}) = a_{x} \cdot b_{x} + a_{y} \cdot b_{y} = 0$ . Получим, что необходимым и достаточным условием перпендикулярности прямых $a$ и $b$ , находящихся в прямоугольной системе координат $О х у$ на плоскости, является $(\vec{a}, \vec{b}) = a_{x} \cdot b_{x} + a_{y} \cdot b_{y} = 0$ , где $\vec{a} = (a_{x}, a_{y})$ и $\vec{b} = (b_{x}, b_{y})$ - это направляющие векторы прямых $a$ и $b$ .

Условие применимо, когда необходимо найти координаты направляющих векторов или при наличии канонических или параметрических уравнений прямых на плоскости заданных прямых $a$ и $b$ .

Пример 1

Заданы три точки $A (8, 6), B (6, 3), C (2, 10)$ в прямоугольной системе координат $О х у$ . Определить, прямые $А В$ и $А С$ перпендикулярны или нет.

Решение

Прямые $А В$ и $А С$ имеют направляющие векторы $\vec{A B}$ и $\vec{A C}$ соответственно. Для начала вычислим $\vec{A B} = (- 2, - 3), \vec{A C} = (- 6, 4)$ . Получим, что векторы $\vec{A B}$ и $\vec{A C}$ перпендикулярны из свойства о скалярном произведении векторов, равном нулю.

$(\vec{A B}, \vec{A C}) = (- 2) \cdot (- 6) + (- 3) \cdot 4 = 0$

Очевидно, что необходимое и достаточное условие выполнимо, значит, $А В$ и $А С$ перпендикулярны.

Ответ: прямые перпендикулярны.

Пример 2

Определить, заданные прямые $\frac{x - 1}{2} = \frac{y - 7}{\sqrt{3}}$ и $\{\begin{cases} x = 1 + λ \\ y = \sqrt{2} - \sqrt{2} \cdot λ \end{cases}$ перпендикулярны или нет.

Решение

$\vec{a} = (2, \sqrt{3})$ является направляющим вектором заданной прямой $\frac{x - 1}{2} = \frac{y - 7}{\sqrt{3}}$ ,

$\vec{b} = (1, - \sqrt{2})$ является направляющим вектором прямой $\{\begin{cases} x = 1 + λ \\ y = \sqrt{2} - \sqrt{2} \cdot λ \end{cases}$ .

Перейдем к вычислению скалярного произведения векторов $\vec{a}$ и $\vec{b}$ . Выражение будет записано:

$(\vec{a}, \vec{b}) = 2 \cdot 1 + \sqrt{3} \cdot (- \sqrt{2}) = 2 - \sqrt{6} \neq 0$

Результат произведения не равен нулю, можно сделать вывод, что векторы не перпендикулярны, значит и прямые также не перпендикулярны.

Ответ: прямые не перпендикулярны.

Необходимое и достаточное условие перпендикулярности прямых $a$ и $b$ применяется для трехмерного пространства, записывается в виде $(\vec{a}, \vec{b}) = a_{x} \cdot b_{x} + a_{y} \cdot b_{y} + a_{z} \cdot b_{z} = 0$ , где $\vec{a} = (a_{x}, a_{y}, a_{z})$ и $\vec{b} = (b_{x}, b_{y}, b_{z})$ являются направляющими векторами прямых $a$ и $b$ .

Пример 3

Проверить перпендикулярность прямых в прямоугольной системе координат трехмерного пространства, заданные уравнениями $\frac{x}{2} = \frac{y}{- 1} = \frac{z + 1}{0}$ и $\{\begin{cases} \begin{array}{l} x = λ \\ y = 1 + 2 \cdot λ \end{array} \\ z = 4 \cdot λ \end{cases}$

Решение

Знаменатели из канонических уравнений прямых считаются координатами направляющего вектора прямой. Координаты направляющего вектора из параметрического уравнения – коэффициенты. Отсюда следует, что $\vec{a} = (2, - 1, 0)$ и $\vec{b} = (1, 2, 4)$ являются направляющими векторами заданных прямых. Для выявления их перпендикулярности найдем скалярное произведение векторов.

Выражение примет вид $(\vec{a}, \vec{b}) = 2 \cdot 1 + (- 1) \cdot 2 + 0 \cdot 4 = 0$ .

Векторы перпендикулярны, так как произведение равно нулю. Необходимое и достаточное условие выполнено, значит прямые также перпендикулярны.

Ответ: прямые перпендикулярны.

Проверка перпендикулярности может проводится, исходя из других необходимых и достаточных условий перпендикулярности.

Теорема 2

Прямые $a$ и $b$ на плоскости считаются перпендикулярными при перпендикулярности нормального вектора прямой $a$ с вектором $b$ , это и есть необходимое и достаточное условие.

Доказательство 2

Данное условие применимо, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых. То есть при наличии общего уравнения прямой вида $A x + B y + C = 0$ , уравнения прямой в отрезках вида $\frac{x}{a} + \frac{y}{b} = 1$ , уравнения прямой с угловым коэффициентом вида $y = k x + b$ координаты векторов возможно найти.

Пример 4

Выяснить, перпендикулярны ли прямые $3 x - y + 2 = 0$ и $\frac{x}{\frac{3}{2}} + \frac{y}{\frac{1}{2}} = 1$ .

Решение

Исходя их уравнений, необходимо найти координаты нормальных векторов прямых. Получим, что $\vec{n_{α}} = (3, - 1)$ - это нормальный вектор для прямой $3 x - y + 2 = 0$ .

Упростим уравнение $\frac{x}{\frac{3}{2}} + \frac{y}{\frac{1}{2}} = 1$ до вида $\frac{2}{3} x + 2 y - 1 = 0$ . Теперь четко видны координаты нормального вектора, которые запишем в такой форме $\vec{n_{b}} = (\frac{2}{3}, 2)$ .

Векторы $\vec{n_{a}} = (3, - 1)$ и $\vec{n_{b}} = (\frac{2}{3}, 2)$ будут перпендикулярными, так как их скалярное произведение даст в итоге значение равное $0$ . Получим $(\vec{n_{a}}, \vec{n_{b}}) = 3 \cdot \frac{2}{3} + (- 1) \cdot 2 = 0$ .

Необходимое и достаточное условие было выполнено.

Ответ: прямые перпендикулярны.

Когда прямая $a$ на плоскости определена при помощи уравнения с угловым коэффициентом $y = k_{1} x + b_{1}$ , а прямая $b$ - $y = k_{2} x + b_{2}$ , отсюда следует, что нормальные векторы будут иметь координаты $(k_{1}, - 1)$ и $(k_{2}, - 1)$ . Само условие перпендикулярности сводится к $k_{1} \cdot k_{2} + (- 1) \cdot (- 1) = 0 \Leftrightarrow k_{1} \cdot k_{2} = - 1$ .

Пример 5

Выяснить, перпендикулярны ли прямые $y = - \frac{3}{7} x$ и $y = \frac{7}{3} x - \frac{1}{2}$ .

Решение

Прямая $y = - \frac{3}{7} x$ имеет угловой коэффициент, равный $- \frac{3}{7}$ , а прямая $y = \frac{7}{3} x - \frac{1}{2}$ - $\frac{7}{3}$ .

Произведение угловых коэффициентов дает значение $- 1, - \frac{3}{7} \cdot \frac{7}{3} = - 1$ , то есть прямые являются перпендикулярными.

Ответ: заданные прямые перпендикулярны.

Имеется еще одно условие, используемое для определения перпендикулярности прямых на плоскости.

Теорема 3

Для перпендикулярности прямых $a$ и $b$ на плоскости необходимым и достаточным условием является коллинеарность направляющего вектора одной из прямых с нормальным вектором второй прямой.

Доказательство 3

Условие применимо, когда есть возможность нахождения направляющего вектора одной прямой и координат нормального вектора другой. Иначе говоря, одна прямая задается каноническим или параметрическим уравнением, а другая общим уравнением прямой, уравнением в отрезках или уравнением прямой с угловым коэффициентом.

Пример 6

Определить, являются ли заданные прямые $x - y - 1 = 0$ и $\frac{x}{0} = \frac{y - 4}{2}$ перпендикулярными.

Решение

Получаем, что нормальный вектор прямой $x - y - 1 = 0$ имеет координаты $\vec{n_{a}} = (1, - 1)$ , а $\vec{b} = (0, 2)$ - направляющий вектор прямой $\frac{x}{0} = \frac{y - 4}{2}$ .

Отсюда видно, что векторы $\vec{n_{a}} = (1, - 1)$ и $\vec{b} = (0, 2)$ не коллинеарны, потому что условие коллинеарности не выполняется. Не существует такого числа $t$ , чтобы выполнялось равенство $\vec{n_{a}} = t \cdot \vec{b}$ . Отсюда вывод, что прямые не являются перпендикулярными.

Ответ: прямые не перпендикулярны.

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.