Уравнение плоскости в отрезках: описание, примеры, решение задач

Данный раздел будет полностью посвящен теме «Уравнение плоскости в отрезках». Мы последовательно рассмотрим, какой вид имеет уравнение плоскости в отрезках, применение этого уравнения для построения заданной плоскости в прямоугольной системе координат, переход от общего уравнения плоскости к уравнению плоскости в отрезках. В статье мы рассмотрим большое количество примеров, которые облегчат усвоение информации.

Уравнение плоскости в отрезках – описание и примеры

Уравнение плоскости в отрезках имеет вид $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$ , где $a, b$ и $c$ – это действительные числа, отличные от нуля. Абсолютные величины чисел $a, b$ и $c$ равны длинам отрезков, которые отсекаются плоскостью на осях координат $Oх$, $Oу$ и $Oz$ в трехмерной системе координат $Oхуz$. Откладываются длины отрезков от начала координат. Направление, в котором необходимо отложить длину отрезка, определяет знак, стоящий перед числом. Наличие «-» свидетельствует о том, что отрезок надо откладывать от нуля в отрицательном направлении оси.

Действительно, координаты точек $\left(a, 0, 0\right), \left(0, b, 0\right), \left(0, 0, c\right)$  удовлетворяют уравнению плоскости в отрезках:

$$\begin{gathered} \frac{a}{a}+\frac{0}{b}+\frac{0}{c}=1=1\iff 1=1 \\ \frac{{\displaystyle 0}}{{\displaystyle a}}+\frac{{\displaystyle b}}{{\displaystyle b}}+\frac{{\displaystyle 0}}{{\displaystyle c}}=1=1\iff 1=1 \\ \frac{{\displaystyle 0}}{{\displaystyle a}}+\frac{{\displaystyle 0}}{{\displaystyle b}}+\frac{{\displaystyle c}}{{\displaystyle c}}=1=1\iff 1=1 \end{gathered}$$

Поясним этот момент, расположив заданные точки на графике.

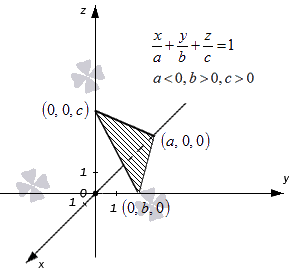
Проиллюстрируем описанное выше примером.

Уравнение плоскости в отрезках удобно использовать для построения чертежей. Проиллюстрируем это утверждение примером.

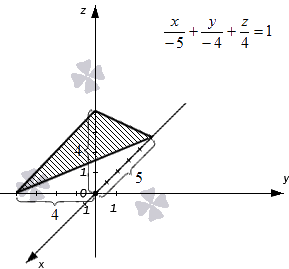
Плоскость может быть задана уравнением плоскости другого вида. Для того, чтобы изобразить заданную плоскость на чертеже, можно сначала перейти к уравнению плоскости в отрезках. Получив уравнение плоскости в отрезках, нам останется лишь отметить точки $\left(a, 0, 0\right), \left(0, b, 0\right), \left(0, 0, c\right)$ и соединить их прямыми линиями.

Приведение общего уравнения плоскости к уравнению плоскости в отрезках

Мы имеем общее уравнение плоскости в пространстве вида $Ax+By+Cz+D=0$ . И мы можем получить уравнение плоскости в отрезках. Сделать это можно в том случае, если плоскость пересекает все координатные оси, причем не в начале координат.

Не получится перевести общее уравнение плоскости в пространстве в уравнение плоскости в отрезках в тех случаях, когда плоскость проходит через одну из координатных осей или располагается параллельно оси. Другими словами, мы можем работать лишь с полным уравнением плоскости вида $Ax+By+Cz+D=0$, где $A\ne 0, B\ne 0, C\ne 0, D\ne 0$ .

Приведение общего уравнения плоскости к уравнению плоскости в пространстве производится следующим образом. Переносим слагаемое $D$ в правую часть уравнения с противоположным знаком.

$Ax+By+Cz+D=0\iff Ax+By+Cz=-D$

Так как $D\ne 0$ , то обе части полученного уравнения можно разделить на $–D$:  $\frac{A}{-D}x+\frac{B}{-D}y+\frac{C}{-D}z=1$ .

Так как $A\ne 0, B\ne 0, C\ne 0$ , то мы можем отправить в знаменатели коэффициенты перед переменными $x, y$ и $z$. Последнее уравнение эквивалентно равенству $\frac{x}{{\displaystyle -\frac{D}{A}}}+\frac{{\displaystyle y}}{{\displaystyle -\frac{D}{B}}}+\frac{{\displaystyle z}}{{\displaystyle -\frac{D}{C}}}=1$ . При этом мы использовали очевидное равенство $\frac{p}{q}=\frac{1}{{\displaystyle \frac{q}{p}}}, p, q\in R, p\ne 0, q\ne 0$ .

В итоге, мы получаем уравнение плоскости в отрезках. Это становится хорошо видно в том случае, если обозначить $-\frac{D}{A}=a, -\frac{D}{B}=b, -\frac{D}{C}=c$.

Разберем решение примера.