Решение целых и дробно рациональных неравенств

Условие: решите целое рациональное неравенство $x·(x+3) +2·x\le (x+1)2+1$.

Решение

Начнем с переноса выражения из правой части в левую с противоположным знаком.

$x·(x+3) +2·x-(x+1)2-1\le 0$

Теперь, когда мы выполнили все действия с многочленами слева, можно переходить к линейному неравенству $3·x-2\le 0$, равносильному тому, что было дано в условии. Решить его несложно:

$$\begin{gathered} 3·x\le 2 \\ x\le \frac{2}{3} \end{gathered}$$

Ответ: $x\le \frac{2}{3}$.

Условие: найдите решение неравенства $(x^2+1{)}^2-3·x^2> (x^2-x) ·(x^2+x)$.

Решение

Переносим выражение из левой части в правую и выполняем дальнейшие преобразования с помощью формул сокращенного умножения.

$$\begin{gathered} (x^2+1{)}^2-3·x^2-(x^2-x)·(x^2+x)>0 \\ {x}^4+2·x^2+1-3·x^2-x^4+x^2>0 \\ 1>0 \end{gathered}$$

В итоге наших преобразований мы получили неравенство, которое будет верным при любых значениях $x$, следовательно, решением исходного неравенства может быть любое действительное число.

Ответ: любое действительно число.

Условие: решите неравенство $x+6+2·x^3-2·x·(x^2+x-5)>0$.

Решение

Из правой части мы ничего переносить не будем, поскольку там $0$. Начнем сразу с преобразования левой части в многочлен:

$$\begin{gathered} x+6+2·x^3-2·x^3-2·x^2+10·x>0 \\ -2·x^2+11·x+6>0. \end{gathered}$$

Мы вывели квадратное неравенство, равносильное исходному, которое легко решить несколькими методами. Применим графический способ.

Начнем с вычисления корней квадратного трехчлена $-2·x^2+11·x+6$:

$$\begin{gathered} D={11}^2-4·(-2)·6=169 \\ {x}_1=\frac{-11+\sqrt{169}}{2·\left(-2\right)}, x_2=\frac{-11-\sqrt{169}}{2·\left(-2\right)} \\ {x}_1=-0,5, x_2=6 \end{gathered}$$

Теперь на схеме отметим все необходимые нули. Поскольку старший коэффициент меньше нуля, ветви параболы на графике будут смотреть вниз.

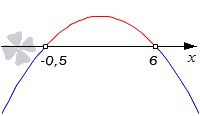
Нам будет нужна область параболы, расположенная над осью абсцисс, поскольку в неравенстве у нас стоит знак $>$. Нужный интервал равен $(-0,5, 6)$, следовательно, эта область значений и будет нужным нам решением.

Ответ: $(-0,5, 6)$.

Условие: вычислите $(x^2+2) ·(x+4) <14-9·x$.

Решение

Начнем, как всегда, с переноса выражения в левую часть, после чего нужно будет выполнить раскрытие скобок и приведение подобных слагаемых.

$$\begin{gathered} (x^2+2)·(x+4)-14+9·x<0 \\ {x}^3+4·x^2+2·x+8-14+9·x<0 \\ {x}^3+4·x^2+11·x-6<0 \end{gathered}$$

В итоге преобразований у нас получилось равносильное исходному равенство, слева у которого стоит многочлен третьей степени. Применим метод интервалов для его решения.

Сначала вычисляем корни многочлена, для чего нам надо решить кубическое уравнение $x^3+4·x^2+11·x-6=0$. Имеет ли оно рациональные корни? Они могут быть лишь в числе делителей свободного члена, т.е. среди чисел $\pm 1, \pm 2, \pm 3, \pm 6$. Подставим их по очереди в исходное уравнение и выясним, что числа $1, 2$ и $3$ будут его корнями.

Значит, многочлен $x^3+4·x^2+11·x-6$ может быть описан в виде произведения $(x-1) ·(x-2) ·(x-3)$, и неравенство $x^3+4·x^2+11·x-6<0$ может быть представлено как $(x-1) ·(x-2) ·(x-3) <0$.  С неравенством такого вида нам потом будет легче определить знаки на промежутках.

Далее выполняем оставшиеся шаги интервального метода: рисуем числовую прямую и точки на ней с координатами $1, 2, 3$. Они разбивают прямую на $4$ промежутка, в которых нужно определить знаки. Заштрихуем промежутки с минусом, поскольку исходное неравенство имеет знак $<$.

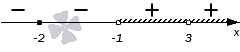
Нам осталось только записать готовый ответ: $(-\infty , 1) \cup (2, 3)$.

Ответ: $(-\infty , 1) \cup (2, 3)$.

Условие: найдите решение неравенства $(x^2-2·x-1) ·(x^2-19) \ge 2·x·(x^2-2·x-1)$.

Решение

Данное неравенство относится к целым. Если мы перенесем выражение из правой части влево, раскроем скобки и выполним приведение слагаемых, то получим $x^4-4·x^3-16·x^2+40·x+19\ge 0$.

Решить такое неравенство непросто, поскольку придется искать корни многочлена четвертой степени. Оно не имеет ни одного рационального корня (так, $1, -1, 19$ или $-19$ не подходят), а искать другие корни сложно. Значит, воспользоваться этим способом мы не можем.

Но есть и другие способы решения. Если мы перенесем выражения из правой части исходного неравенства в левую, то сможем выполнить вынесение за скобки общего множителя $x^2-2·x-\mathrm{1:}$

$\mathrm{}$$$\begin{gathered} (x^2-2·x-1)·(x^2-19)-2·x·(x^2-2·x-1)\ge 0 \\ (x^2-2·x-1)·(x^2-2·x-19)\ge 0. \end{gathered}$$

Мы получили неравенство, равносильное исходному, и его решение даст нам искомый ответ. Найдем нули выражения в левой части, для чего решим квадратные уравнения $x^2-2·x-1=0$ и $x^2-2·x-19=0$.  Их корни – $1\pm \sqrt{2}, 1\pm 2\sqrt{5}$. Переходим к равенству $\left(x-\left(1+\sqrt{2}\right)\right)·\left(x-\left(1-\sqrt{2}\right)\right)·\left(x-\left(1+2\sqrt{5}\right)\right)·\left(x-\left(1-2\sqrt{5}\right)\right)\ge 0$, которое можно решить методом интервалов:

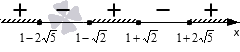
Согласно рисунку, ответом будет $\left(-\infty ,1-2\sqrt{5}\right]\cup \left[1-2\sqrt{5}, 1+\sqrt{2}\right]\cup \left[1+2\sqrt{5}, +\infty \right]$.

Ответ: $\left(-\infty ,1-2\sqrt{5}\right]\cup \left[1-2\sqrt{5}, 1+\sqrt{2}\right]\cup \left[1+2\sqrt{5}, +\infty \right]$.

Условие: найдите решения рационального равенства $\frac{x}{\left(x+1\right)·\left(x-3\right)}+\frac{4}{{\displaystyle {\left(x-3\right)}^2}}\ge \frac{-3·x}{{\displaystyle {\left(x-3\right)}^2}{\displaystyle ·}{\displaystyle \left(x+1\right)}}$.

Решение

Действуем по алгоритму, указанному выше. Сначала определяем область допустимых значений. В данном случае она определяется системой неравенств $\left\{\begin{array}{l}\begin{array}{l}\left(x+1\right)·\left(x-3\right)\ne 0\\ {\left(x-3\right)}^2\ne 0\end{array}\\ {\left(x-3\right)}^2·(x+1)\ne 0\end{array}\right.$, решением которой будет множество $(-\infty , -1)\cup (-1, 3)\cup (3, +\infty )$.

Далее нам надо сделать так, чтобы в правой части неравенства получился $0$. Выполняем перенос выражения из правой части влево с противоположным знаком и получаем неравенство, равносильное исходному:

$\frac{x}{\left(x+1\right)·\left(x-3\right)}+\frac{4}{(x-3{)}^2}+\frac{3·x}{(x-3{)}^2·(x+1)}\ge 0$

После этого нам нужно преобразовать его так, чтобы было удобно применить метод интервалов. Первым делом приводим алгебраические дроби к наименьшему общему знаменателю $(x-3{)}^2·(x+1)$:

$$\begin{gathered} \frac{x}{\left(x+1\right)·\left(x-3\right)}+\frac{4}{(x-3{)}^2}+\frac{3·x}{(x-3{)}^2·(x+1)}= \\ =\frac{x·\left(x-3\right)+4·\left(x+1\right)+3·x}{{\left(x-3\right)}^2·\left(x+1\right)}=\frac{x^2+4·x+4}{(x-3{)}^2·(x+1)} \end{gathered}$$

Сворачиваем выражение в числителе, применяя формулу квадрата суммы:

$\frac{x^2+4·x+4}{{\left(x-3\right)}^2·\left(x+1\right)}=\frac{{\displaystyle {\left(x+2\right)}^2}}{{\displaystyle {\left(x-3\right)}^2}{\displaystyle ·}{\displaystyle \left(x+1\right)}}$

Областью допустимых значений получившегося выражения является $(-\infty ,-1) \cup (-1, 3) \cup (3, +\infty )$. Мы видим, что она аналогична той, что была определена для исходного равенства. Заключаем, что неравенство $\frac{{\displaystyle {\left(x+2\right)}^2}}{{\displaystyle {\left(x-3\right)}^2·\left(x+1\right)}}\ge 0$ является равносильным исходному, значит, последний шаг алгоритма нам не нужен.

Используем метод интервалов:

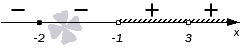
Видим решение $\{-2\}\cup (-1, 3)\cup (3, +\infty )$, которое и будет решением исходного рационального неравенства $\frac{x}{\left(x+1\right)·\left(x-3\right)}+\frac{4}{{\displaystyle {\left(x-3\right)}^2}}\ge \frac{-3·x}{(x-3{)}^2·(x+1)}$.

Ответ: $\{-2\} \cup (-1, 3) \cup (3, +\infty )$.

Условие: вычислите решение $\frac{{\displaystyle \frac{x+3}{x}-1-\frac{3}{x}}}{x+2}+\frac{2}{x-1}>\frac{1}{x+1}+2·\frac{x+2}{x^2-1}$.

Решение

Определяем область допустимых значений. В случае с этим неравенством она будет равна всем действительным числам, кроме $-2,-1, 0$ и $1$.

Переносим выражения из правой части в левую:

$\frac{{\displaystyle \frac{x+3}{x}-1-\frac{3}{x}}}{x+2}+\frac{2}{x-1}-\frac{1}{x+1}-2·\frac{x+2}{x^2-1}>0$

Далее выполняем преобразование левой части. Сначала преобразуем первую дробь:

$\frac{{\displaystyle \frac{x+3}{x}-1-\frac{3}{x}}}{x+2}=\frac{{\displaystyle \frac{x+3-x-3}{x}}}{x+2}=\frac{{\displaystyle \frac{0}{x}}}{x+2}=\frac{0}{x+2}=0$

Учитывая получившийся результат, запишем:

$$\begin{gathered} \frac{{\displaystyle \frac{x+3}{x}-1-\frac{3}{x}}}{x+2}+\frac{2}{x-1}-\frac{1}{x+1}-2·\frac{x+2}{x^2-1}= \\ =0+\frac{2}{x-1}-\frac{1}{x+1}-2·\frac{x+2}{x^2-1}= \\ =\frac{2}{x-1}-\frac{1}{x+1}-2·\frac{x+2}{x^2-1}= \\ =\frac{2}{x-1}-\frac{1}{x+1}-2·\frac{x+2}{(x+1)·\left(x-1\right)}= \\ =\frac{-x-1}{(x+1)·\left(x-1\right)}=-\frac{x+1}{(x+1)·\left(x-1\right)}=-\frac{1}{x-1} \end{gathered}$$

Для выражения $-\frac{1}{x-1}$ областью допустимых значений будет множество всех действительных чисел, за исключением единицы. Мы видим, что область значений расширилась: в нее были добавлены $-2, -1$ и $0$. Значит, нам нужно выполнить последний шаг алгоритма.

Поскольку мы пришли к неравенству $-\frac{1}{x-1}>0$, можем записать равносильное ему $\frac{1}{x-1}<0$. С помощью метода интервалов вычислим решение и получим $(-\infty , 1)$.

Исключаем точки, которые не входят в область допустимых значений исходного равенства. Нам надо исключить из$(-\infty , 1)$ числа $-2, -1$ и $0$.  Таким образом, решением рационального неравенства $\frac{{\displaystyle \frac{x+3}{x}-1-\frac{3}{x}}}{x+2}+\frac{2}{x-1}>\frac{1}{x+1}+2·\frac{x+2}{x^2-1}$ будут значения $(-\infty , -2)\cup (-2, -1)\cup (-1, 0)\cup (0, 1)$.

Ответ: $(-\infty , -2) \cup (-2, -1) \cup (-1, 0) \cup (0, 1)$.

Условие: найдите решение неравенства $\frac{5+{\displaystyle \frac{3}{x^2}}}{{\displaystyle \frac{x^3+1}{x^2-x+1}-\frac{x^2-1}{x-1}}}\ge 0$.

Решение

Область допустимых значений неравенства, заданного в условии, определяет система $\left\{\begin{array}{l}\begin{array}{l}{x}^2\ne 0\\ x^2-x+1\ne 0\end{array}\\ \begin{array}{l}x-1\ne 0\\ \frac{x^3+1}{x^2-x+1}-\frac{x^2-1}{x-1}\ne 0\end{array}\end{array}\right.$.

Решений у этой системы нет, поскольку

$$\begin{gathered} \frac{x^3+1}{x^2-x+1}-\frac{x^2-1}{x-1}= \\ =\frac{(x+1)·\left(x^2-x+1\right)}{x^2-x+1}-\frac{(x-1)·\left(x+1\right)}{x-1}= \\ =x+1-(x+1)=0 \end{gathered}$$

Значит, исходное равенство $\frac{5+{\displaystyle \frac{3}{x^2}}}{{\displaystyle \frac{x^3+1}{x^2-x+1}-\frac{x^2-1}{x-1}}}\ge 0$ не имеет решения, поскольку нет таких значений переменной, при которой оно имело бы смысл.

Ответ: решений нет.