- 16 июля 2025
- 7 минут
- 9 413
Решение уравнений высших степеней
Статью подготовили специалисты образовательного сервиса Zaochnik.
В общем случае уравнение, имеющее степень выше , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.
Уравнения высшей степени с целыми коэффициентами
Все уравнения, имеющие вид , мы можем привести к уравнению той же степени с помощью умножения обеих частей на и осуществив замену переменной вида :
Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид .
Схема решения уравнения
Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде . Здесь является корнем уравнения, а представляет собой частное от деления на .
Подставляем остальные выписанные делители в , начав с , поскольку корни могут повторяться. После получения тождества корень считается найденным, а уравнение может быть записано в виде .Здесь будет частным от деления на .
Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как . После этого исходное уравнение можно представить как . Здесь является многочленом --ной степени. Для подсчета удобно использовать схему Горнера.
Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.
У нас в итоге получилось уравнение , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.
Покажем на конкретном примере, как применяется такая схема решения.
Условие: найдите решение уравнения .
Решение
Начнем с нахождений целых корней.
У нас есть свободный член, равный минус трем. У него есть делители, равные и . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.
При , равном единице, мы получим , значит, единица будет корнем данного уравнения.
Теперь выполним деления многочлена на в столбик:
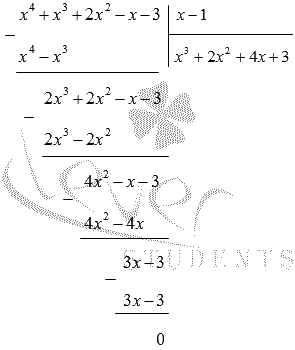
Значит, .
Перебираем возможные делители дальше, но подставляем их в равенство :
У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный .
Делим многочлен на в столбик:
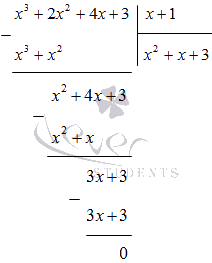
Получаем, что
Подставляем очередной делитель в равенство , начиная с :
Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.
Оставшиеся корни будут корнями выражения .
Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: .
Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.
| коэффициенты многочлена | |||||
В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, .
После нахождения следующего корня, равного , мы получаем следующее:
| коэффициенты многочлена | ||||
Далее мы приходим к разложению . Потом, проверив оставшиеся делители равенства , вычисляем оставшиеся корни.
Ответ: , .
Условие: решите уравнение .
Решение
У свободного члена есть делители .
Проверяем их по порядку:
Значит, будет корнем уравнения. Разделим на , воспользовавшись схемой Горнера:
| коэффициенты многочлена | |||||
В итоге мы получим .
Проверяем делители дальше, но уже для равенства , начиная с двойки.
Значит, опять будет корнем. Разделим на :
| коэффициенты многочлена | ||||
В итоге получим .
Проверка оставшихся делителей смысла не имеет, поскольку равенство быстрее и удобнее решить с помощью дискриминанта.
Решим квадратное уравнение:
Получаем комплексно сопряженную пару корней: .
Ответ: .
Условие: найдите для уравнения действительные корни.
Решение
Выполняем домножение обеих частей уравнения:
Заменяем переменные :
В итоге у нас получилось стандартное уравнение -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет действительных корня и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут и .
Ответ: ,
Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени.
Математические онлайн-калькуляторы




